一种圆锯片及其制备方法与流程

本发明涉及石材等硬脆材料加工技术，具体为一种圆锯片及其制备方法。
背景技术：
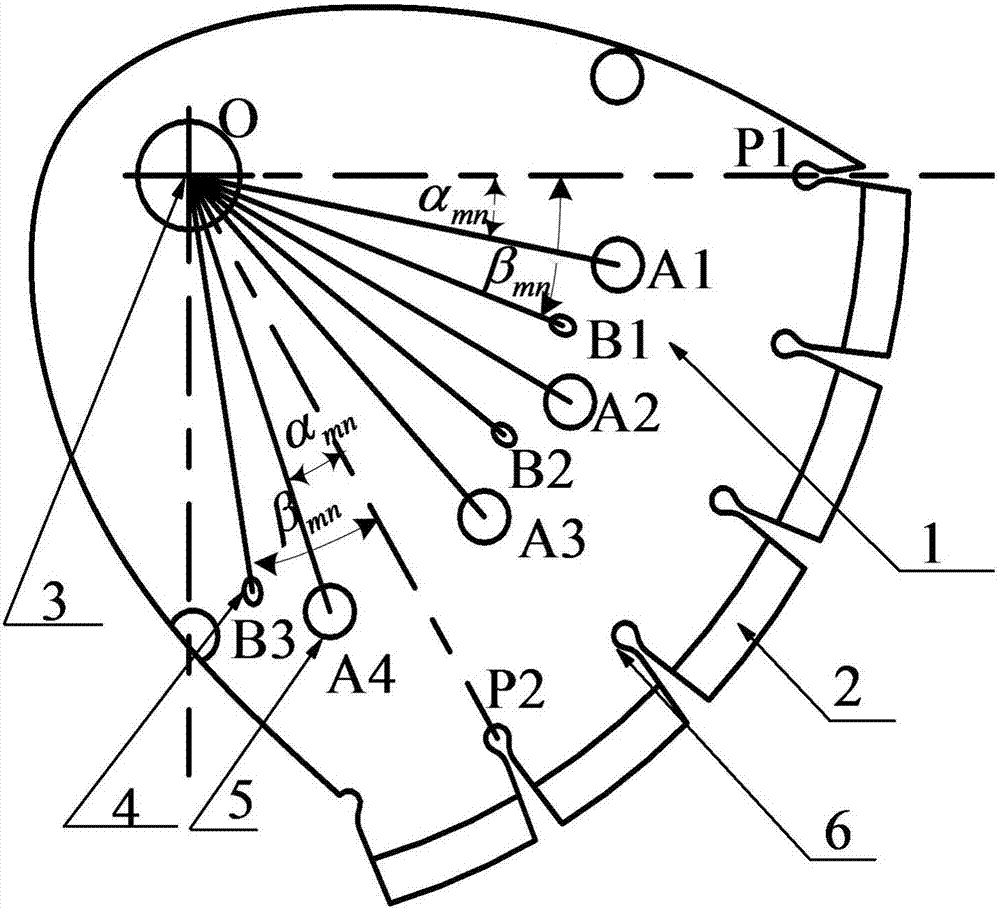
：随着现代化工业的发展，噪声污染越来越严重，已成为世界公害。根据ISO等效连续噪声A声级与听力损伤危险率关系及中国《工业企业噪声卫生标准》得出，以10年工龄计算，在80～85dB(A)噪声暴露下，会造成轻微的听力损伤，损伤率3％；在85～90dB(A)，会造成13％噪声性耳聋；在90～100dB(A)之间，听力损伤者约为20％，在100～115dB(A)之间，听力损伤者超过32％。噪声污染不仅损伤听力，而且对神经系统和心血系统造成严重影响。金刚石圆锯片锯切石材过程中，主要噪声源为机械噪声，由于金刚石锯齿刀头周期性与工件相互摩擦及冲击，相当于锯片受到持续的动态激励，从而使锯片产生剧烈振动并伴随有强烈的噪声。普通金刚石圆锯片锯切石材时的噪声声压级水平可达105～110dB(A)，而基体拓扑优化开减振孔得到的低噪声金刚石圆锯片在相同条件下可降低噪声声压水平达10～15dB(A)。目前，低噪声圆锯片的制备方法主要有三种：一是改变基体结构，在基体上用激光加工特定槽或孔，槽或孔中可填充高阻尼材料；二是复合圆锯片，由两个薄刚片组成，中间用高耗能材料粘合作为基体，通过振动衰减实现降低噪声的目的；三是反馈控制技术，主要由电磁设备及振动传感器组成，系统根据反馈的锯片横向位移按照比例调节电磁导向装置，从而达到在线自动调控，降低锯片横向振动目的。基体开减振孔圆锯片是用激光切割机在锯片基体上切割出挖空的减振孔结构，其降噪机理是锯片产生的振动波被孔隔断，从而消减了基体的振动及噪声共鸣反弹；阻尼夹层圆锯片由于结构的固有频率改变可消除圆锯片空载时的“啸声”，同时夹层材料阻尼特性可以吸收振动能量从而降低锯切时的噪声，然而在实际工作中常因周向焊接不牢而开裂；并且锯片基体局部高温可导致夹层材料变质，严重影响降噪效果。反馈控制低噪声锯片的控制系统成本过高，安装复杂，现阶段市场化推广困难。从工艺成本和技术水平上综合考虑，基体开减振孔实现锯片低噪声化是目前最好的选择方式。近些年，基于锯片基体开孔减振降噪机理，形成了多种基体拓扑方式，如鱼钩形、圆孔、雨点型孔等等。传统的拓扑研究凭借经验或者多采用在静载荷或准静态载荷等简单载荷条件下，以模型静态响应作为边界条件，基于灵敏度梯度分析等方法对锯片进行拓扑开孔，然后获得减振降噪的锯片开孔结构。然而，石材锯切过程十分复杂，锯片与石材相互干涉运动产生振动载荷，应用传统梯度方法在动载条件下优化困难，其原因：一方面，动态优化问题涉及的边界条件复杂，特别是非线性振动问题、结构和工件间的复杂交互作用问题、结构塑性变形以及结构形态设计的庞大自由度问题，计算量大，使得问题求解困难。另一方面，非线性激励条件下结构动力学响应问题，主要表现在对于动态锯片的计算分析困难，锯片响应量与设计变量的关系确定难以解决。技术实现要素：针对现有技术的不足，本发明拟解决的技术问题是，提供一种圆锯片及其制备方法。该圆锯片基体上开有拓扑优化减振孔，可有效降低石材锯切过程噪声的辐射强度，减小环境污染压力。该制备方法具有计算相对简单，工业化实施容易，易于实际推广等特点。本发明解决所述圆锯片技术问题的技术方案是：设计一种圆锯片，由圆形合金基体及其周向边缘均布焊接的金刚石锯齿刀头组成，相邻金刚石锯齿刀头之间开有水槽，圆形合金基体中心开有安装孔，其特征在于所述安装孔与金刚石锯齿刀头之间的圆形合金基体上按区域周向均布开有大减振孔和小减振孔，所述大减振孔和小减振孔是通过动态拓扑优化设计方法对旋转圆锯片优化后获得的挖空结构，所述动态拓扑优化设计是将锯切石材过程中圆锯片的非线性振动信息作为边界条件，结合混合元胞自动机算法，依据优化目标，开展的圆锯片动态拓扑优化设计。本发明解决所述制备方法技术问题的技术方案是：设计一种本发明所述圆锯片的制备方法。该制备方法包括以下工序：(1)合金基体材料的选择与制备；(2)金刚石锯齿刀头与合金基体之间过渡层的制备；(3)金刚石锯齿刀头的制备；(4)金刚石锯齿刀头与圆形合金基体的焊接；(5)拓扑优化设计减振孔结构；(6)圆形合金基体按所优化设计的减振孔进行激光开孔；所述拓扑优化设计减振孔结构采用混合元胞自动机动态优化方法进行优化，并通过以下步骤实现：①定义设计区域；②把设计域离散为元胞单元，建立元胞单元与有限元网格单元一一映射的关系，即实现设计区域混合元胞自动机模型的建立；③对设计域材料进行参数化构建；④定义优化目标函数，约束条件以及收敛准则；⑤采用显示动力学程序对圆锯片切割石材过程进行非线性动力学分析，记录单元内部能量以及锯片表面的位移、速度非线性振动信息；⑥根据动态锯切模型响应数据，计算每个元胞场变量信息，根据目标函数以及约束条件，借助元胞自动机局部规则更新元胞状态，通过对材料的密度重新分布，实现单元的增加或删除；⑦最后检验迭代过程是否收敛，当满足收敛标准后计算结束，得到最终拓扑结构；若不满足迭代过程，重复运算上述②～⑦，直至满足。与现有技术相比，本发明圆锯片利用混合元胞自动机动态算法实施拓扑优化的低噪声减振孔圆锯片降噪效果明显。本发明制备方法将锯切石材过程中圆锯片的非线性振动信息作为边界条件，通过混合元胞自动机动态拓扑优化方法指导了低噪声圆锯片开减振孔的设计，并具有良好推广性，工业化容易实施的特点。符合绿色制造业产品的设计，为锯切过程锯片的噪声及振动控制提供了有效的方法。附图说明图1是本发明圆锯片一种实施例的形状结构示意图。图2是本发明圆锯片一种实施例的金刚石锯齿刀头、水槽及优化所得挖空的减振孔局部图。图3是本发明圆锯片制备方法一种实施例的工艺流程图。图4是本发明圆锯片制备方法一种实施例的开减振孔的设计可行域。图5是本发明圆锯片制备方法一种实施例的开减振孔拓扑优化设计所采用的流程图。图6是普通圆锯片与经过本发明设计方法优化后的开减振孔金刚石圆锯片切割石材噪声频率-声压响应特性比较图。其中，图6(a)是普通圆锯片锯切石材的噪声频率-声压幅频响应特性曲线；图6(b)是经过混合元胞自动机算法拓扑优化金刚石锯片锯切石材时噪声频率-声压幅频响应特性曲线。其中，图5优化的减振孔结构为图3开减振孔锯片制备提供开孔设计图样。具体实施方式下面结合实施例及其附图对本发明作进一步详细说明。本发明设计的圆锯片(参见图1、2、4)，由圆形合金基体(简称基体)1及其周向边缘均布焊接的金刚石锯齿刀头2组成，相邻金刚石锯齿刀头2之间开有水槽6，基体1中心开有安装孔3，其特征在于所述安装孔3与金刚石锯齿刀头2之间的基体1上按区域周向均布开有大减振孔4和小减振孔5，所述大减振孔4和小减振孔5是通过动态拓扑优化设计方法对旋转圆锯片优化后获得的挖空结构，所述动态拓扑优化设计是将锯切石材过程中圆锯片的非线性振动信息作为边界条件，结合混合元胞自动机算法，依据优化目标，开展的圆锯片动态拓扑优化设计。本发明圆锯片上所开的大减振孔4和小减振孔5可以是相同形状，也可以是不同形状，实施例的大减振孔4为圆形孔，小减振孔5为径向为长轴的椭圆形孔。实施例的圆形减振孔的半径为12mm，开孔位于基体1的外圈；椭圆形减振孔的长轴为3mm、短轴为2mm，开孔位于基体1的内圈。所述大、小减振孔4、5的开孔个数分别为k1、k2(k≥1)。所述大、小减振孔4、5的减振孔结构以及孔的个数随不同工程实况，由优化程序自适应、自组织和自修复迭代得到。实施例的开孔个数k1＝18，k2＝12。所述大、小减振孔4、5中可单独某一个或两个同时填充阻尼材料。实施例将设计域分为6等份(参见图4)，由PmOPm+1围绕(m＝1,2,3…，6，P1、P7重合)。在每个子设计域所述的大减振孔4有3个，大减振孔4在每个子设计域沿周向均匀分布，每个大减振孔4之间的相对角度∠PmOBn＝αmn(第m个子区域中αmn＝10°，30°，50°其中，n＝3m-2，3m-1，3m)；在每个子设计域所述的小减振5孔有2个，小减振孔5在每个子设计域沿周向均匀分布，每个小减振孔5之间的相对角度∠PmOBn＝βmn(第m个子区域中n＝2m-1，2m；βmn＝20°、40°)。本发明同时设计了所述金刚石圆锯片的制备方法(参见图3、5)，该制备方法包括以下步骤：(1)合金基体1材料的选择与制备；(2)金刚石锯齿刀头2与合金基体1之间过渡层的制备；(3)金刚石锯齿刀头2的制备；(4)金刚石锯齿刀头2与圆形合金基体1的焊接；(5)拓扑优化设计减振孔结构；(6)圆形合金基体1按所优化设计的减振孔(包括大、小减振孔4、5)进行激光开孔；所述拓扑优化设计减振孔结构采用混合元胞自动机动态优化方法进行优化，并通过以下步骤实现：其中，步骤(1)～(4)、(6)基本为现有技术。本发明制备方法主要创新特征在于步骤(5)，拓扑优化设计减振孔结构。本发明所述的大、小减振孔4、5需要采用混合元胞自动机算法进行优化。在基体的拓扑优化过程中，首先建立动态锯切有限元模型，并实现设计域有限元网格与元胞自动机网格一一映射，根据设计域元胞的状态以及局部优化设计准则，通过不断变化重新分布元胞的密度进行删除或者添加单元，在保证结构刚度需求条件下，最终获得以锯片表面速度均方响应的极小值为设计目标的优化结构。本发明基于混合元胞自动机算法进行基体开减振孔的设计优化具体实施过程如下(参见图5)：(1)定义设计区域。所述的金刚石锯片在满足锯片锯切强度及保证锯片夹盘的安装要求条件下，设计锯片开减振孔的设计区域为锯片半径2/5～4/5之间区域，其设计可行域如图4中阴影区域所示，为保证优化结构所得结构具有对称性，以满足锯切稳定性要求，将设计域等分为ABCD围绕的6个相同子区域(参见图4)。图4中7为满足圆锯片夹盘安装所留区域，区域范围为圆锯片半径2/5以内区域。(2)离散锯切模型。优化过程中设计域网格单元与元胞单元一一映射的关系，共同组成混合元胞自动机网格模型。元胞自动机算法用于计算设计域中材料的密度分布情况，有限元算法用于分析因材料分布而引起的模型结构的变化。元胞自动模型是由元胞栅格组成的，每个元胞栅格都一个状态值，并且任意元胞i状态在某一步长t是特定的，在此时刻元胞i的状态根据局部控制规则使得该元胞状态只取决于上一步长t-1元胞的状态以及相邻的所有元胞的状态，这种局部控制规则随时间增加不断对体系内各元胞同步更新，通过该规则以简单离散的元胞来考察整个体系行为，可以免除拓扑优化过程中对于梯度信息的处理，能够很好应用于复杂动态加载方式的拓扑优化问题。混合元胞自动机算法中，单个元胞状态是由设计变量相对密度和场变量内能能量密度进行定义，表达为：σi＝{xi(t),Ui}[1][1]式中，xi单元相对密度；Ui为状态变量。针对动态旋转锯片工作过程中整体安全性问题，本发明方法引入内能能量密度作为元胞状态变量，内部能量密度可量化为变形所储存的机械能，结构刚度越大，它能储存的应变能越低。设计域元胞在迭代优化演化过程中，逐步使非空元胞趋于内能饱和状态，当元胞单元的内部能量密度达到运行最大值时，所得的结构不但满足刚度需求，同时满足所设定减振降噪目标及约束条件。单元相对密度的更新规则如[2]式：xi(k+1)=xi(k)+K(Uit-U*)/U*---[2]]]>[2]式中，xi单元相对密度，K为缩放因子，为考虑邻近元胞状态的内能密度平均值，U*单元局部内能密度目标值。(3)设计域材料参数化。材料参数化是拓扑优化的基础，拓扑过程最终目标的实现是对设计域材料根据优化算法在目标函数及约束函数条件下有选择性地进行去除和保留操作，并按照规则重新排列，得到具有减振降噪性能的圆锯片。本质上是使用插值模型分布0-1离散变量的优化过程，0代表零密度单元(单元去除)，1代表满密度单元(单元保留)。为保证锯片设计域材料在优化过程中实现最优化分布，本方案选用变密度SIMP插值函数表达材料的分布。该材料参数方法通过式[3]的惩罚因子对单元中间密度进行惩罚，使中间密度向0/1逼近，可有效的避免拓扑布局出现的棋盘格、局部极值等不稳定现象。决定设计域材料空间单元属性的杨氏模量、屈服强度以及应变硬化模量在迭代过程中与材料密度数学关系如下:ρ(xi)=xiρ0E(xi)=xipE0σ(xi)=xiqσ0Eh(xi)=xiqEh0---[3]]]>[3]式中，0≤xi≤1为离散单元相对密度(1代表单元满材料，0代表空)，ρ为单元密度，E代表杨氏模量，为p、q为惩罚因子；σ和Eh为屈服强度及应变硬化模量，该材料属性代表了基体材料的非线性特性。(4)设计目标。高速旋转锯片在锯切石材过程结构表面辐射噪声能量可表示为：W=ρc·σrad·S·<V2‾>---[4]]]>[4]式中：ρc为空气特性阻抗，σrad为振动表面声辐射系数，S为振动表面面积，为锯片表面质点法向振动时空均方值。因此，锯切过程金刚石锯片噪声功率级可描述为：L=10log(W/W0)=10logρc+10logS+10log<V2‾>+10logAσrad-10logW0---[5]]]>[5]式中，A为声级加权系数，W0为声功率基准。[5]式中，若空气特性阻抗ρc为常数，声辐射比σrad若为常数，圆锯片表面振动与空气介质振动叠加产生的声辐射只与法向振动时空均方值有关。可知，金刚石锯片减振降噪优化问题可以转化为求解锯片表面法向振动速度均方极小值。石材锯切过程中，刀具与石材间复杂动态交互作用会导致锯片发生轴向变形，为避免刀具轴向变形过大，会引起锯片的受力不均，导致剧烈振动，为满足结构刚度需求，根据加工条件限制锯片刀头轴向挠度位移最大值为wmax；过大切割力直接导致刀具加剧磨损，根据实际加工条件，限制总锯切力载荷最大值不超Fmax；为了上述满足结构的约束需求，选取拓扑优化的最终质量参数为Mp。结合上述描述，拓扑优化的数学模型可以表达为：MinΠ=Σi=1nSiVi2S]]>S.T.d<wmaxF<FmaxΣi=1Nρivi<Mp0<ρi≤1---[6]]]>[6]式中，i为优化前后保持不变的单元编号，Vi为单元i的表面法向振动速度均值，Si为单元i的表面积，S为锯片有效表面积。d为最大横向位移，F为横向切割力，M为设计域锯片的初始质量，ρi、vi分别为设计域单元的相对密度、体积。(5)以有限元模式将金刚石锯片、夹盘以及石材组成一个系统，建立动态锯切模型。锯切系统边界条件：圆盘锯片施加固定转速、进给速度，并对工件两侧边界施加X、Y、Z方向全约束。(6)根据动态锯切模型响应数据，计算每个元胞场变量信息，根据目标函数以及约束条件，借助元胞自动机局部规则更新元胞状态，通过对材料的密度重新分布，实现单元的增加或删除。(7)为了避免迭代过早收敛，定义两次迭代间元胞的质量(密度)变化之和小于收敛因子，如式[7]所述：ΔM(K)=Σi=1N|xi(k+1)-xi(k)|ΔM(K)+ΔM(K-1)2<ϵ1---[7]]]>[7]式中，ε1为质量收敛因子，为元胞密度。若达到收敛准则，输出最优拓扑结构；否则，迭代代数K＝K+1，重复步骤(2)～(7)。本发明圆锯片的明显降噪效果可以从图6的对比实验研究结果得到证明(参见图6)：图6(a)为普通金刚石圆锯片锯切石材噪声频率-声压响应特性图；图6(b)为本发明低噪声开减振孔圆锯片锯切石材噪声频率-声压响应特性图。如图6所示，当激励频率接近金刚石圆锯片固有频率时，频率-声压响应曲线中会出现典型的振幅跳跃的非线性现象，系统产生共振，从而响应幅值增大。对比分析图6(a)和图6(b)可知，经过拓扑优化后的基体开减振孔金刚石圆锯片，在150Hz共振频率下的振动幅值降低了约85％，在1000Hz共振频率下的振动幅值降低了约40％，在3000Hz左右共振频率下的振动幅值降低了约60％，在4500HZ左右共振频率下的振动幅值降低了约43％，本发明圆锯片降噪效果明显。可以看出，在[2000～4000Hz]对人体噪声影响最敏感频率段内，引入混合元胞自动机算法优化后的锯片在相应共振频率下的振动幅值大幅度降低，噪声峰值有高强度的“单峰”转成较低强度“多峰”现象，实现了能量的衰减分散，其最大降低相对幅值为60％。优化拓扑减振降噪效果明显，验证了引进混合元胞自动机算法在锯片动态拓扑优化的可行性和功能效果。本发明在低噪声锯片优化设计领域引入混合元胞自动机算法可有效降低石材锯切过程噪声的辐射强度，减小环境污染压力。本发明未述及之处适用于现有技术。当前第1页1 2 3