一种基于铝空气电池液管理模型的控制与优化策略

：本发明属于金属空气电池领域，涉及一种基于铝空气电池液管理模型的控制与优化策略。

背景技术

0、
背景技术：

1、由于越来越严重的传统能源短缺问题，世界各国不得不去寻找新的替代品，新能源被给予了很大的希望，铝空气电池作为一种“面向21世纪的绿色能源”拥有一般空气电池在便携性及可作为备用电源的优势，同时它也有着自身独特的优点：如原料价格低廉，无毒，比能量大，质量更轻等。因而成为众多国内外专家关注的焦点，有着非常光明的发展前景和非常巨大的市场价值的潜力，在国家大力倡导战略性新兴产业发展的前提下，它也必将国家新能源发展提供可靠的支持。

2、对铝空气电池的输出性能的研究，必须考虑到工作环境的影响，因此对操作条件的研究非常必要且十分迫切的，而目前对这方面的研究还是比较匮乏。而且在有限的对操作条件研究的文献中大多通过大量的放电实验对输出性能进行测算，需要借助精度较高的实验设备才能实现，但此过程不可避免的会对电池本身产生损伤。同时对于一些优化方面的探索如果仅从实验出发而没有理论设计会使得工作内容十分繁复，造成效率低下等问题。

技术实现思路

0、
技术实现要素：

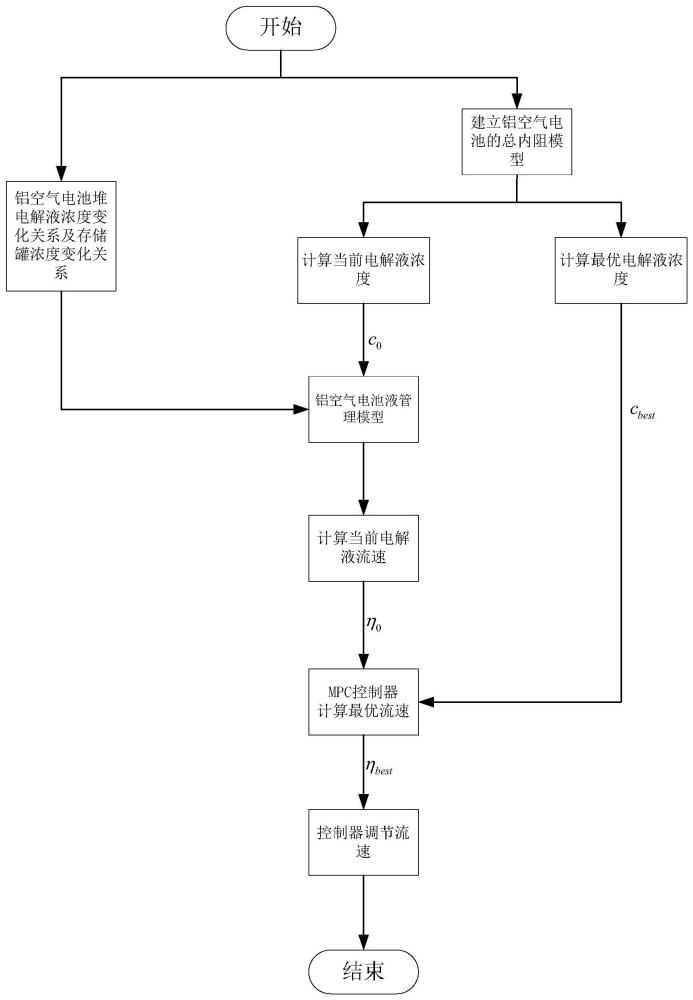
1、为解决相关技术中存在的上述问题，本说明书提供了一种理论上的架构寻找出一条对电解液浓度控制和优化的路径，即基于流速优化的铝空气电池的电解液浓度控制策略，包括：从铝空气电池电解液浓度在电池堆和电解液存储罐中的变化方程导出电解液浓度表达式；通过交流阻抗测试仪测量铝空气电池堆工作状态下的实时电阻，继而建立铝空气电池堆的总内阻模型，控制温度和电流密度不变，计算当前工况下的电解液浓度，代入上述的电解液浓度表达式从而计算当下的电解液流速，同时根据内阻模型求出在总内阻最小的情况下的电解液浓度，定义为最优浓度；利用mpc算法定义目标函数进行模型预测、优化问题求解、应用控制输入经过不断地系统演化得以不断调整流速，以维持浓度在最优浓度附近，这种方法允许考虑系统动态性质和未来时间段内的优化控制，提高了对系统变化和不确定性的适应能力；该设计包括以下步骤：

2、步骤1：建立铝空气电池的电解液管理模型；建立的铝空气电解液管理模型基于假设：电解质和电流均匀地分布在电池组内不同的电池中，活性物质均匀地分布在所有电池中，并且在充电(放电)过程中变化到相同的程度，且没有离子穿过膜，没有自放电反应；如此得到铝空气电池的液管理模型为：

3、

4、式中，vcl代表铝空气电池堆的体积,vtk代表电解液存储罐的体积,l；k代表电池堆中的电池的数量；z代表单位活度系数；f代表法拉第常数；i代表施加到电池的电流,a；η代表电解液的流速，m/s；t代表时间，s；ccell代表铝空气电池堆的电解液浓度,a0代表罐中电解液的初始浓度,b0代表电池堆电解液的初始浓度,mol/l；

5、步骤2：建立铝空气电池堆的总内阻模型；根据铝空气电池电极的极化现象将所产生的内阻划分为活化内阻rf，欧姆内阻rm，浓差内阻rd；其中所述铝空气电池的活化内阻rf关于温度和电流密度的表达式为：

6、

7、所述铝空气电池的欧姆内阻rm关于温度和电解液浓度的表达式为：

8、

9、所述铝空气电池的浓差内阻rd关于温度和电流密度的表达式为：

10、

11、

12、铝空气总内阻模型用rstack表示，令rstack＝rf+rm+rd，故：

13、

14、式中,i代表工作电流密度，i0为参考状态下交换电流密度，a/cm2；α为电荷转移系数；n为电化学反应转移电荷数；δg为电化学反应活化能；tcell为工作温度，t0为参考温度,k；f为法拉第常数；r为理想气体常数；ccell为电池堆中的电解液浓度,mol/l；s为电解液的截面积，cm2；β1、β2、β3分别为模型的仿真参数；l为电池宽度，cm；δ为扩散层厚度，μm；cg表示反应物总浓度，mol/l；d0为标准扩散常数；ε表示多孔电极孔隙率；

15、通过交流阻抗测试仪向铝空气电池堆发送0.1hz低频信号，测出当前温度和电流密度下的总内阻rstack值，将测得的rstack值代入公式(6)，计算当前工况下的电解液浓度c0并代入公式(1)，保持电流大小不变，选取电解液流速作为控制变量来控制电解液浓度，得到当前的电解液流速η0；

16、步骤3：同时在当前温度和电流密度下，基于rstack最小求出最优的电解液浓度cbest，具体的计算方式为总内阻模型rstack在当前工况下对c求偏导等于0得到，即方程：

17、

18、解得：

19、根据所建立的液管理模型(1)可以得到浓度c与流速η之间的关系，可写成如下形式：

20、cpredicted(i+1)＝f(c(i),η(i))

21、其中i是预测时域中的时间步，优化目标可以表示为：

22、

23、其中n是优化时间步的数量；根据实际条件确保流速η在合理的范围内，即：

24、ηmin≤η≤ηmax

25、利用梯度下降法来求解上述优化问题，梯度下降法的规则可以表述为：

26、

27、其中α是学习率，在每个时间步，需要计算代价函数关于控制输入的梯度，即然后使用梯度下降法来更新控制输入，迭代进行整个过程，直到满足收敛条件，得到最优的流速ηoptimal,并将最优的流速应用于系统，最后重复以上步骤，根据系统模型模拟系统相应，更新浓度和流速的实际值直到达到所需要的控制时间步数。

28、通过流速的变化达到对电解液浓度快速且准确地调节，实现输出性能的提高。

技术特征：

1.一种基于铝空气电池液管理模型的控制与优化策略，其特征在于，包括：

2.根据权利要求1所述的方法，结合式(2)可以认识到rstack值是随c的变化先减小后增大，有且仅有一个转折浓度，最优电解液浓度cbest通过权利要求1所述的总内阻模型rstack在定电流密度和温度的情况下对c求偏导等于0得到，即方程：

技术总结
本发明提出了一种基于铝空气电池液管理模型的控制与优化策略，针对传统的优化策略通过大量实验找到最优电解液浓度的不足，考虑到总内阻是影响输出性能的根本原因，选择在总内阻最小的情况下的电解液浓度为最优的电解液浓度。首先建立电解液浓度的表达式，即铝空气的液管理模型，同时建立总内阻模型，了解各种操作条件对总内阻的影响，控制温度和电流密度不变，求出最优的电解液浓度，将此电解液浓度代入液管理模型中求出在最优的电解液浓度下的电解液的流速，利用MPC算法将最优电解液浓度与实际工作状态下的电解液流速作为输入参数并定义目标函数进行模型预测、求解优化问题，应用控制输入经过不断地系统演化得以不断调整流速，最终实现输出性能的优化。此方法简单有效，可以提高铝空气电池的能量利用效率，具有一定的实用价值和应用前景。

技术研发人员：莫伟杰,向志平,卫东
受保护的技术使用者：中国计量大学
技术研发日：
技术公布日：2024/11/18