非迭代菲涅耳纯相位全息图生成和复用方法、装置及介质

本发明涉及三维全息，具体涉及一种非迭代菲涅耳纯相位全息图生成和复用方法。

背景技术：

1、全息术可以在二维(2d)全息图上记录光波的三维(3d)信息，并从全息图中再现三维信息。与光学全息显示相比，计算全息三维投影显示具有制作简单、效率高、成本低和便于信息的存储和传输等显著优点，不仅可以显示静态的实物，而且可以显示虚拟动态物体。三维计算全息主要的挑战是对连续三维空间中的每个物体点进行菲涅耳衍射模拟所需的巨大计算成本。同时在许多实时动态全息显示系统中，需要进行高速计算来生成计算全息图(computer generated hologram，cgh)，计算效率成为了限制三维计算全息发展的瓶颈。

2、目前常用的三维cgh方法有：点云法，多边形法和分层法。点云法中3d对象可以表示为独立作用的自发光点光源的集合，其主要缺点是高计算复杂性。由于实体形状的表示需要极其精细的采样，因此在某些情况下计算时间可能是不可接受的。多边形法使用平面基元光源表示对象表面，由于多边形平面相对于全息图平面倾斜，因此描述平行平面之间波场传播的公式不直接适用于cgh的合成，需要旋转变换才能将多边形的平面与平行于全息图的平面相关联，增加了计算复杂性。分层法根据不同的深度范围将3d场景切片成层，然后生成各个层的全息图，最终的全息图是所有层全息图贡献的总和，实现了较大的深度范围。

3、经典3d相位全息图的生成方法是迭代菲涅尔变换算法(iterative fresneltransform，ifrta)。该方法基于gerberch和saxton提出的gerberch-saxton(gs)算法。将gs算法中傅里叶变换替换为菲涅耳变换(fresnel transform，frt)后，即所谓的迭代菲涅耳变换算法(ifrta)。但ifrta只能针对单一对象生成全息图，当该方法应用在三维全息显示时，需要对各层分别迭代生成全息图，非常耗时。2021年，alejandro velez zea等人提出了一种优化的菲涅尔随机相位(optimization fresnel random phase，ofrap)方法，用于生成菲涅耳纯相位全息图。菲涅耳全息图具有允许选择重建平面的优点，并且可以消除重建系统中对透镜的需要，从而降低其成本和复杂性。ofrap具有与目标窗口相同的支撑，但目标的支撑集的大小以及光学系统的参数不能改变。否则，需要生成新的ofrap。

技术实现思路

1、本发明提出的一种非迭代菲涅耳纯相位全息图生成和复用方法，可至少解决上述技术问题之一。

2、为实现上述目的，本发明采用了以下技术方案：

3、一种非迭代菲涅耳纯相位全息图生成和复用方法，包括以下步骤，

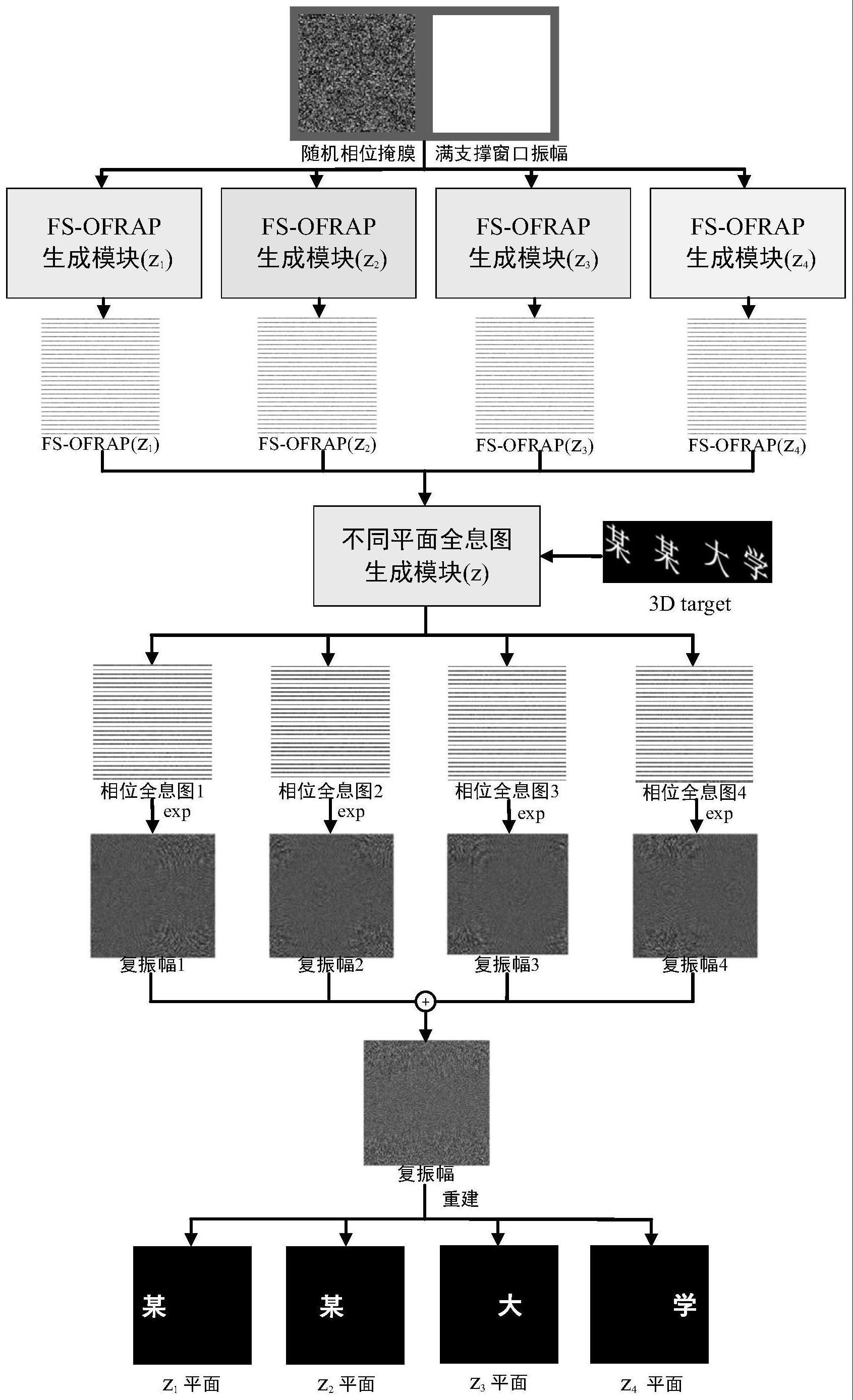
4、首先，利用迭代菲涅尔方法生成不同平面的fs-ofraps，再结合3d物体分层策略非迭代生成不同层对应的全息图，通过叠加或复用得到最终的相位全息图，最后将复用后的全息图重建得到三维目标物体。

5、进一步的，所述利用迭代菲涅尔方法生成不同平面的fs-ofraps，包括首先满支撑单位振幅和随机相位掩模相乘后进行逆菲涅尔变换，接着遵循迭代菲涅尔算法做循环的多次迭代，生成fs-ofrap。

6、进一步的，所述利用迭代菲涅尔方法生成不同平面的fs-ofraps还包括，生成多张对应各层的fs-ofrap，即使用相同的输入，经过不同距离参数z的fs-ofrap生成模块，最终生成每层对应的fs-ofrap。

7、进一步的，所述再结合3d物体分层策略非迭代生成不同层对应的全息图，具体包括，

8、对三维物体沿深度方向进行等间距分层处理，将分层后的二维截面图与其相对应距离的fs-ofrap合成复振幅，进行菲涅尔逆变换，非迭代生成每层的纯相位全息图。

9、进一步的，所述通过叠加或复用得到最终的相位全息图，包括将各层生成的相位全息图转化成复振幅进行叠加或复用，生成该3d目标的相位全息图。

10、进一步的，复用方式有叠加复用和空分复用。

11、进一步的，叠加复用方法是将全息图复振幅直接相加生成复用全息图；设有n个全息图复振幅，则叠加复用方法公式如下：

12、

13、其中，fj(x,y)＝exp[iφj(x,y)]，表示第j个全息图对应的复振幅，φj(x,y)为第j个相位全息图，最终提取叠加后复振幅m(x,y)的相位得到复用全息图。

14、进一步的，空分复用是分割空间进行复用；首先，将slm划分为n个区域，每个区域放置各层全息图复振幅，放置位置对应选取放置区域在原全息图复振幅的位置；将每个子样本放置在它们各自的相对原始位置。

15、另一方面，本发明公开一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，所述计算机程序被所述处理器执行时，使得所述处理器执行如权上述方法的步骤。

16、再一方面，本发明还公开一种计算机可读存储介质，存储有计算机程序，所述计算机程序被处理器执行时，使得所述处理器执行如上述方法的步骤。

17、由上述技术方案可知，由于传统的三维全息显示主要通过迭代生成全息图，生成时间长且重建质量差，本发明结合满支撑优化菲涅尔随机相位(fs-ofrap)和三维物体分层思想，提出了一种三维非迭代相位全息图的满支撑优化菲涅尔随机相位方法(three-dimensional full support optimization fresnel random phase，3d-fs-ofrap)。首先，利用迭代菲涅尔方法生成不同平面的fs-ofraps，再结合3d物体分层策略非迭代生成不同层对应的全息图，最后通过叠加或复用得到最终的相位全息图。通过数值实验和光学实验验证了本发明的3d-fs-ofrap方法的有效性。

18、本发明提出了一种三维满支撑优化菲涅尔随机相位(3d-fs-ofrap)方法，可以直接实现用于三维全息显示的纯相位全息图的快速生成。该方法突破了原始ofrap方法在空间域中目标振幅固定支撑的大小和位置的限制，可以在非迭代方式下实现大尺寸3dcgh的快速生成。数值实验和光学实验验证了本发明3d-fs-ofrap方法的优越性。

技术特征：

1.一种非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于，包括以下步骤，

2.根据权利要求1所述的非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于：所述利用迭代菲涅尔方法生成不同平面的fs-ofraps，包括首先满支撑单位振幅和随机相位掩模相乘后进行逆菲涅尔变换，接着遵循迭代菲涅尔算法做循环的多次迭代，生成fs-ofrap。

3.根据权利要求2所述的非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于：所述利用迭代菲涅尔方法生成不同平面的fs-ofraps还包括，生成多张对应各层的fs-ofrap，即使用相同的输入，经过不同距离参数z的fs-ofrap生成模块，最终生成每层对应的fs-ofrap。

4.根据权利要求1所述的非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于：所述再结合3d物体分层策略非迭代生成不同层对应的全息图，具体包括，

5.根据权利要求4所述的非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于：所述通过叠加或复用得到最终的相位全息图，包括将各层生成的相位全息图转化成复振幅进行叠加或复用，生成该3d目标的相位全息图。

6.根据权利要求5所述的非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于：

7.根据权利要求6所述的非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于：

8.根据权利要求6所述的非迭代菲涅耳纯相位全息图生成和复用方法，其特征在于：空分复用是分割空间进行复用；首先，将slm划分为n个区域，每个区域放置各层全息图复振幅，放置位置对应选取放置区域在原全息图复振幅的位置；将每个子样本放置在它们各自的相对原始位置。

9.一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，所述计算机程序被所述处理器执行时，使得所述处理器执行如权利要求1至8中任一项所述方法的步骤。

10.一种计算机可读存储介质，存储有计算机程序，所述计算机程序被处理器执行时，使得所述处理器执行如权利要求1至8中任一项所述方法的步骤。

技术总结
本发明的一种非迭代菲涅耳纯相位全息图生成和复用方法、设备及介质，包括以下步骤，首先，利用迭代菲涅尔方法生成不同平面的FS‑OFRAPs，再结合3D物体分层策略非迭代生成不同层对应的全息图，通过叠加或复用得到最终的相位全息图，最后将复用后的全息图重建得到三维目标物体。本发明可以直接实现用于三维全息显示的纯相位全息图的快速生成。该方法突破了原始OFRAP方法在空间域中目标振幅固定支撑的大小和位置的限制，可以在非迭代方式下实现大尺寸3DCGH的快速生成。数值实验和光学实验验证了本发明3D‑FS‑OFRAP方法的优越性。

技术研发人员：张成,韩鹏,周昊,史继森,吴峰,章权兵,程鸿,沈川
受保护的技术使用者：安徽大学
技术研发日：
技术公布日：2024/1/13