一种基于相邻交叉耦合的升沉补偿平台多缸同步控制方法

1.本发明属于升沉补偿平台领域，涉及多缸同步控制技术，具体涉及一种基于相邻交叉耦合的升沉补偿平台多缸同步控制方法。


背景技术：

2.目前我国海上风电场的设计寿命一般为25年，对于沿海风电场来说，海况相对稳定。而对于远洋风电场来说，在进行海上作业时，因海风和海浪的作用无法避免的产生横摇、纵摇、艏摇、横荡、纵荡、垂荡六个自由度的运动，这些干扰会影响海上风电场的稳定运行以及延长风机平台与船舶之间的可作业时间。六个自由度的升沉补偿平台搭载舷梯可有效隔离载体上的运动，提供一个相对稳定的工作平台。研究如何使平台处于相对稳定的运动状态至关重要。
3.六自由度升沉补偿平台共有六个相同的液压伺服通道，为保证平台的稳定，需要对六个液压缸进行同步控制，使六个液压缸协调运动。目前对于多缸同步控制这一方面获得了很多的科研成果。但仍存在以下几个方面的不足：
4.1、采用诸如偏差耦合、环形耦合、相邻交叉耦合的同步控制策略能够降低控制结构的复杂性，即使存在大干扰时也能快速的响应，且能对跟踪误差进行补偿，这样使得同步控制精度也会有所提高。目前在多电机同步控制系统中应用较多，但是在液压伺服系统中的工程应用较少；
5.2、工程上使用的多缸同步的液压系统，其基本原理没有太大的差别，电液伺服阀的性能对系统性能影响很大，同步系统的精度在一定的程度上受限于元件的特性。
6.3、多缸同步控制不仅存在过冲大、过渡过程中同步精度低、系统可靠性低等问题，且液压伺服系统中存在诸如非线性、参数不确定性、模型不确定性等的影响。
7.所以，需要一个新的技术方案来解决上述问题。


技术实现要素：

8.发明目的：为了克服现有技术中存在的不足，提供一种基于相邻交叉耦合的升沉补偿平台多缸同步控制方法，其采用相邻交叉耦合的同步控制方式，引入耦合系数和同步系数，使每个液压子通道考虑相邻的各个液压缸的同步误差和同步误差分量，使液压子系统内部耦合，结合广义预测控制算法，将同步误差以及同步误差分量引入算法采用的二次性能指标中，从而对六个液压伺服通道进行同步控制，提高系统的同步控制精度以及同步控制性能，使各个液压缸不会因接收到不同的船舶姿态控制信号而发生不协调运动，保证升沉补偿平台的稳定运作。
9.技术方案：为实现上述目的，本发明提供一种基于相邻交叉耦合的升沉补偿平台多缸同步控制方法，包括如下步骤：
10.s1：建立基于carima模型的平台液压伺服系统数学模型；
11.s2：基于相邻交叉耦合控制方式，引入耦合系数和相邻液压缸之间的同步系数，建
立自身液压缸以及与其相邻的两个液压缸的同步误差和同步误差分量；
12.s3：采用广义预测控制算法，在其二次性能指标函数中引入相邻两个液压缸的同步误差和同步误差分量得到新的控制律作用于各个液压缸，实现多缸同步控制。
13.进一步地，所述步骤s1中carima模型的获取方式为：
14.平台液压伺服系统包括伺服放大器、电液伺服阀、液压缸和位移传感器，根据阀控非对称缸的流量连续性方程、阀的流量方程以及液压缸和负载的力平衡方程以及主要元件传递函数建立系统的位置传递函数模型，将其采样离散化并转化为carima模型。
15.进一步地，所述步骤s1中平台液压伺服系统数学模型的建立方法为：
16.将伺服放大器视为比例增益ka；位移传感器将位移信号转化为电压信号，将位移传感器的比例系数视为kf；将电液伺服阀看作为二阶振荡环节，其传递函数为：
[0017][0018]
式(1)中k
sv
为电液伺服阀的流量增益，w
sv
为电液伺服阀的固有频宽，ζ
sv
为电液伺服阀的阻尼比；
[0019]
阀的线性化流量方程、伺服阀到液压缸的流量连续性方程、液压缸的输出力与负载力平衡方程可表示为如下形式：
[0020][0021]
式(2)中，q
l
为负载流量；kc为滑阀流量压力系数；p
l
为负载压力；c
ip
为液压缸内泄漏系数；v1为液压缸无杆腔的容积；βe为有效体积弹性模量；a1、a2分别为液压缸无杆腔和有杆腔的有效作用面积；p1、p2分别为液压缸无杆腔和有杆腔压力；x
p
为活塞杆位移，bp为粘性阻尼系数；f
l
为理论负载力，k为负载刚度；
[0022]
工程上将忽略弹性负载时的执行元件和被控对象视为一个积分与二阶环节的组合；液压缸的传递函数为：
[0023][0024]
式(3)中，a1为液压缸的有效作用面积，ξh为液压缸-负载质量系统的阻尼比， wh为液压缸-负载质量系统的固有频率；
[0025]
由式(1)-式(3)可得电液伺服系统的位置开环传递函数为：
[0026][0027]
将电液位置伺服系统的开环传递函数进行采样离散化处理，并进行平移，得到系
统的输入输出模型差分方程：
[0028][0029]
由式(5)可得
[0030][0031]
根据系统的差分方程，可知na,nb的阶次；则基于carima模型的电液伺服系统可表示为如下形式：
[0032]
a(z-1
)yi(k)＝b(z-1
)ui(k-1)+c(z-1
)ξ(k)/(1-z-1
) (7)
[0033]
式(7)中本发明中c(z-1
)＝1。
[0034]
进一步地，所述步骤s2中同步误差和同步误差分量的定义如下：
[0035]
采用相邻交叉耦合控制方式，使每个液压子系统与其相邻两个液压缸子系统之间相互耦合，由于各个液压系统接收到的位姿控制信号有所不同，故在同步误差中引入耦合系数和同步系数，对于相邻两个液压缸之间的同步误差ε
i,i+1
,ε
i,i-1
和同步误差分量定义如下：
[0036][0037]
式(8)中为相邻液压缸的输出位移，m
i,i+1
,m
i,i-1
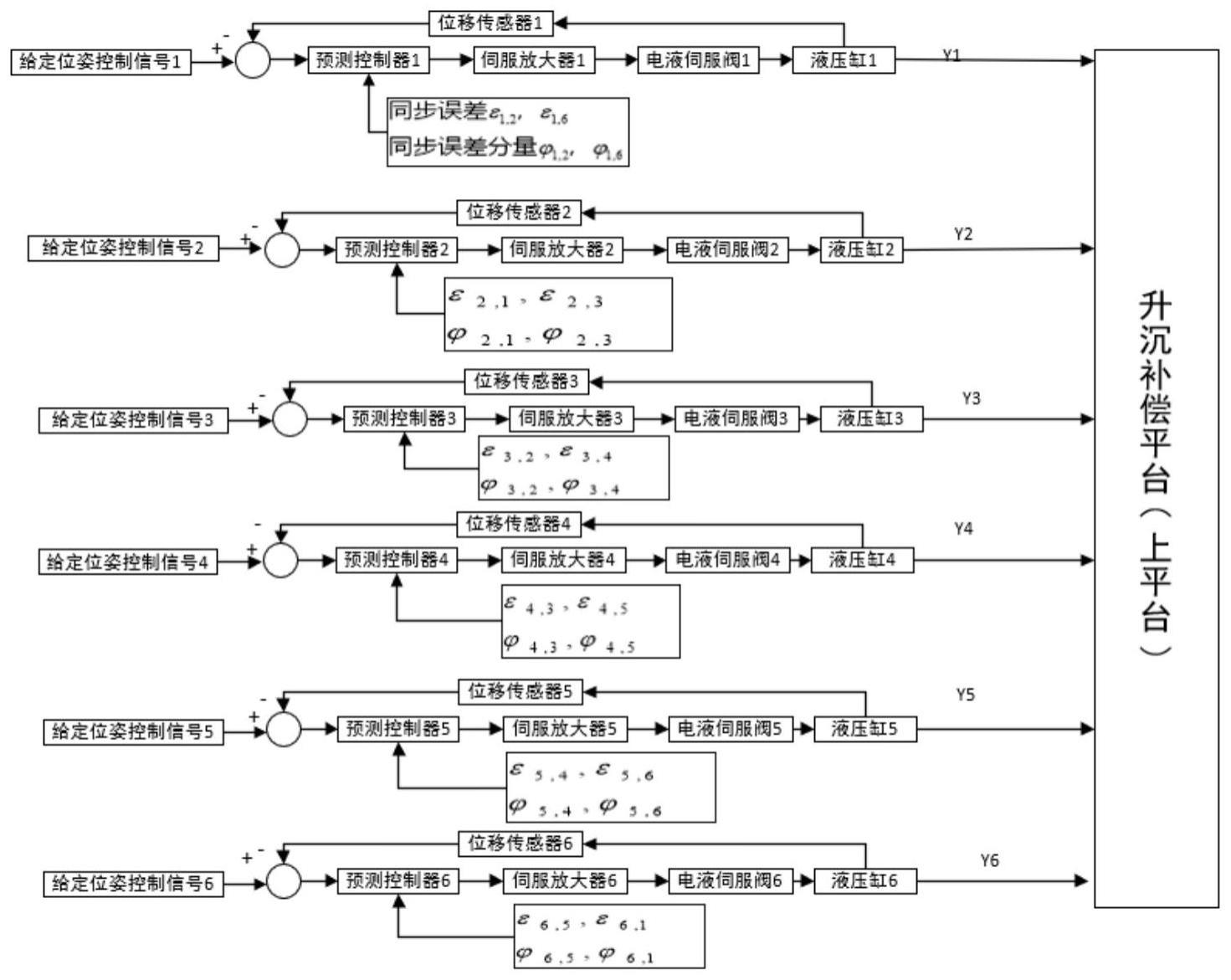
为同步系数，ri为各个液压缸接收的位姿信号，当位姿信号相同时，同步系数就为1，耦合系数为1故省略给出；同步误差φ
i,i+1
,φ
i,i-1
和同步误差分量ψ
i,i+1
,ψ
i,i-1
的矩阵形式可表示为如下形式：
[0038]
[0039]
式(9)中
[0040]
为同步误差分量矩阵，np为预测长度；
[0041]
当液压缸自身的跟随误差、与其相邻两个液压缸的同步误差ε
i,i+1
,ε
i,i-1
，同步误差分量都趋向于0时，可认为六个液压缸输出同步。
[0042]
进一步地，所述步骤s3中引入相邻两个液压缸的同步误差和同步误差分量的二次性能指标函数具体为：
[0043]
选取的各个二次性能指标函数包含自身的跟随误差、控制增量以及自身液压缸分别与其相邻两个液压缸之间的同步误差和同步误差分量，表达形式如下：
[0044][0045]
式(10)中，y
i*
(k+j|k)为每个系统基于k时刻和以前时刻的输入输出数据对未来 k+j时刻系统的最佳输出预测；y
ri
(k+j)为未来k+j时刻的期望输出，δui为控制增量； e为数学期望，k1,k2；β1,β2分别为影响同步误差和同步误差分量的补偿系数，适当增大同步补偿系数可减小同步误差，λi是影响跟踪误差的控制加权因子。
[0046]
当λi＞0时，二次性能指标函数可表示为如下矩阵形式：
[0047][0048]
式(11)中δui(k)＝[δui(k),δui(k+1),
…
,δui(k+n
u-1)]
t
；
[0049]
通过将二次性能指标函数极小化可求得每个液压伺服系统的控制增量δui(k)，从而获得各液压伺服通道的控制量。
[0050]
为计算简便本发明这里以液压子系统一为例求其控制量，此时的性能指标函数包含液压缸一分别与液压缸二和液压缸六之间的同步误差和同步误差分量，其矩阵形式为：
[0051][0052]
将式(12)极小化得到如下形式：
[0053][0054]
式(13)中η1＝k1i+β1p
t
p,η2＝k2i+β2p
t
p，取式(13)矩阵的第一行记为液压伺服通道一得控制增量δu1(k)，则得到k时刻液压伺服通道一所需的控制量为过去时刻控制量和当前时刻控制增量的和即为：
[0055]
u1(k)＝u1(k-1)+δu1(k)
ꢀꢀ
(14)
[0056]
以此方式类推，即可得到其余液压伺服通道的控制增量δui(k)，从而获得各液压伺服通道的控制量为：
[0057]
ui(k)＝ui(k-1)+δui(k)
ꢀꢀ
(15)
[0058]
有益效果：本发明与现有技术相比，采用相邻交叉耦合控制方式，考虑耦合系数和同步系数，在系统中补偿相邻液压缸的同步误差和同步误差分量，采用广义预测控制算法，在其二次性能指标函数中引入同步误差和同步误差分量，从而提高了系统的同步控制精度、动态响应速率，并且降低了系统的静态误差和不稳定性，提高了多通道之间的协调性能，使升沉补偿平台能够稳定运作。
附图说明
[0059]
图1为本发明方法的控制结构示意图；
[0060]
图2为电液伺服阀控非对称缸的结构示意图；
[0061]
图3为无同步系数、无扰动情况下，垂荡运动控制下各个液压缸的跟踪误差仿真图；
[0062]
图4为无同步系数、无扰动情况下，垂荡运动控制下各个液压缸的同步误差仿真图；
[0063]
图5为无同步系数、无扰动情况下，艏摇运动控制下各个液压缸的跟踪误差仿真图；
[0064]
图6为无同步系数、无扰动情况下，艏摇运动控制下各个液压缸的同步误差仿真
图；
[0065]
图7为无同步系数、无扰动情况下，纵荡、纵摇运动控制下各个液压缸的跟踪误差仿真图；
[0066]
图8为无同步系数、无扰动情况下，纵荡、纵摇运动控制下各个液压缸的同步误差仿真图；
[0067]
图9为无同步系数、无扰动情况下，横荡、横摇运动控制下各个液压缸的跟踪误差仿真图；
[0068]
图10为无同步系数、无扰动情况下，横荡、横摇运动控制下各个液压缸的同步误差仿真图；
[0069]
图11为有同步系数、无扰动情况下，艏摇运动控制下各个液压缸的同步误差仿真图；
[0070]
图12为有同步系数、无扰动情况下，横荡、横摇运动控制下各个液压缸的同步误差仿真图；
[0071]
图13为有同步系数、无扰动情况下，纵荡、纵摇运动控制下各个液压缸的同步误差仿真图；
[0072]
图14为在有同步系数和扰动情况下，垂荡运动控制下各个液压缸的同步误差仿真图；
[0073]
图15为在有同步系数和扰动情况下，艏摇运动控制下各个液压缸的同步误差仿真图；
[0074]
图16为在有同步系数和扰动情况下，纵荡、纵摇运动控制下各个液压缸的同步误差仿真图；
[0075]
图17为在有同步系数和扰动情况下，横荡、横摇运动控制下各个液压缸的同步误差仿真图。
具体实施方式
[0076]
下面结合附图和具体实施例，进一步阐明本发明，应理解这些实施例仅用于说明本发明而不用于限制本发明的范围，在阅读了本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本技术所附权利要求所限定的范围。
[0077]
本发明提供一种基于相邻交叉耦合的升沉补偿平台多缸同步控制算法，参照图1，其包括如下步骤：
[0078]
s1：建立基于carima模型的平台液压伺服系统数学模型：
[0079]
如图2所示为电液伺服阀控非对称缸的结构示意图，系统以惯性负载为主，无弹性负载，采用单出杆液压缸，液压伺服系统主要包括伺服放大器、电液伺服阀、液压缸和位移传感器，最重要的就是阀控缸系统，图2中的1-4是输入和输出程阀控缸系统的负载流量，根据阀控非对称缸的流量连续性方程、阀的流量方程以及液压缸和负载的力平衡方程以及主要元件传递函数建立系统的位置传递函数模型，将其采样离散化并转化为 carima模型。
[0080]
数学模型的建立方法具体为：
[0081]
伺服放大器可视为比例增益ka；位移传感器将位移信号转化为电压信号，位移传感器的比例系数可视为kf：电液伺服阀看作为二阶振荡环节，其传递函数为：
[0082][0083]
式(1)中k
sv
为电液伺服阀的流量增益，w
sv
为电液伺服阀的固有频宽，ζ
sv
为电液伺服阀的阻尼比；
[0084]
阀的线性化流量方程、伺服阀到液压缸的流量连续性方程、液压缸的输出力与负载力平衡方程可表示为如下形式：
[0085][0086]
式(2)中，q
l
为负载流量；kc为滑阀流量压力系数；p
l
为负载压力；c
ip
为液压缸内泄漏系数；v1为液压缸无杆腔的容积；βe为有效体积弹性模量；a1、a2分别为液压缸无杆腔和有杆腔的有效作用面积；p1、p2分别为液压缸无杆腔和有杆腔压力；x
p
为活塞杆位移，bp为粘性阻尼系数；f
l
为理论负载力，k为负载刚度；
[0087]
工程上将忽略弹性负载时的执行元件和被控对象视为一个积分与二阶环节的组合；液压缸的传递函数为：
[0088][0089]
式(3)中，a1为液压缸的有效作用面积，ξh为液压缸-负载质量系统的阻尼比， wh为液压缸-负载质量系统的固有频率；
[0090]
由式(1-3)可得液压系统的位置开环传递函数为：
[0091][0092]
将系统的开环传递函数进行采样离散化处理，并进行平移，得到系统的输入输出模型差分方程：
[0093][0094]
由式(5)可得
[0095][0096]
根据系统的差分方程，可知na,nb的阶次；则基于carima模型的电液伺服系统可表示为如下形式：
[0097]
a(z-1
)yi(k)＝b(z-1
)ui(k-1)+c(z-1
)ξ(k)/(1-z-1
)
ꢀꢀ
(7)
[0098]
s2：基于相邻交叉耦合控制方式，考虑耦合系数和相邻两个液压缸之间的同步系
数，建立自身液压缸以及与其相邻的两个液压缸的同步误差和同步误差分量：
[0099]
采用相邻交叉耦合控制方式，使每个液压子系统与其相邻两个液压缸子系统之间相互耦合，由于船舶有六个自由度方向上的运动，各个液压系统接收到的位姿控制信号有所不同，故在同步误差中引入耦合系数和同步系数，对于相邻两个液压缸之间的同步误差ε
i,i+1
,ε
i,i-1
和同步误差分量定义如下：
[0100][0101]
式(8)中为相邻液压缸的输出位移，m
i,i+1
,m
i,i-1
为同步系数，ri为各个液压缸接收的位姿信号，当位姿信号相同时，同步系数就为1。耦合系数为1故省略给出。同步误差φ
i,i+1
,φ
i,i-1
和同步误差分量ψ
i,i+1
,ψ
i,i-1
的矩阵形式可表示为如下形式：
[0102][0103]
式(9)中
[0104]
为同步误差分量矩阵，np为预测长度。
[0105]
当液压缸自身的跟随误差、与其相邻两个液压缸的同步误差ε
i,i+1
,ε
i,i-1
，同步误差分量都趋向于0时，可认为六个液压缸输出同步。
[0106]
s3：基于步骤s2的所定义的同步误差和同步误差分量，采用广义预测控制算法，在
其二次性能指标函数中引入相邻两个液压缸的同步误差和同步误差分量得到新的控制律作用于各个液压缸，其具体步骤如下：
[0107]
选取的各个二次性能指标函数包含自身的跟随误差、控制增量以及自身液压缸分别与其相邻两个液压缸之间的同步误差和同步误差分量，表达形式如下：
[0108][0109]
式(10)中，y
i*
(k+j|k)为每个系统基于k时刻和以前时刻的输入输出数据对未来 k+j时刻系统的最佳输出预测；y
ri
(k+j)为未来k+j时刻的期望输出，δui为控制增量；e为数学期望，k1,k2；β1,β2分别为影响同步误差和同步误差分量的补偿系数，适当增大同步补偿系数可减小同步误差，λi是影响跟踪误差的控制加权因子，当λi＞0时，性能指标函数可表示为如下矩阵形式：
[0110][0111]
式(11)中δui(k)＝[δui(k),δui(k+1),
…
,δui(k+n
u-1)]
t
；通过将性能指标函数极小化可求得每个液压伺服系统的控制增量δui(k)。
[0112]
为计算简便本实施例以液压子系统一为例求其控制量，此时的性能指标函数包含液压缸一分别与液压缸二和液压缸六之间的同步误差和同步误差分量，其矩阵形式为：
[0113]
将式(12)极小化得到如下形式：
[0114][0115]
式(13)中η1＝k1i+β1p
t
p,η2＝k2i+β2p
t
p，取式(13)矩阵的第一行记为液压伺服通道一得控制增量δu1(k)，则得到k时刻液压伺服通道一所需的控制量为过去时刻控制量和当前时刻控制增量的和即为：
[0116]
u1(k)＝u1(k-1)+δu1(k)
ꢀꢀ
(14)
[0117]
以此方式类推，即可得到其余液压伺服通道的控制增量δui(k)，从而获得各液压伺服通道的控制量为：
[0118]
ui(k)＝ui(k-1)+δui(k)
ꢀꢀ
(15)
[0119]
基于上述技术方案，为了验证本发明方法的效果，进行如下仿真实验：
[0120]
在matlab中仿真设计预测控制器的性能，选取电液伺服阀控非对称称液压缸系统的参数为：液压缸无杆腔直径d＝50mm，有杆腔直径为d＝36mm，有效行程为280mm，单个液压缸的惯性负载mt＝60kg，液压缸-负载质量系统的阻尼比ξh＝0.15；液压油的体积弹性模量βe＝0.7
×
109pa；液压缸两腔的总容积v
t
＝2.7
×
10-3
m3；电液伺服阀的固有频率ω
sv
＝85hz，阻尼比ξ
sv
＝0.8，额定流量qsv＝30l/min，额定控制电流为ic＝8ma，阀的流量增益k
sv
＝0.0625m3/(s
·
a)；液压缸的有效作用面积为a1＝1.96
×
10-3
m2[0121]
根据液压伺服系统的数学模型对输出进行预测，在matlab中进行仿真，采用广义预测控制的仿真参数为：控制参数λi为25，预测时域5，输出柔化系数0.2。仿真其在不同位姿控制信号下的跟踪误差和同步误差，所输入的控制信号都为阶跃信号。
[0122]
船舶运动的六个自由度分别为垂荡、艏摇、纵荡、纵摇、横荡、横摇。如图3～图 10所示，在垂荡情况下，液压缸接收的位姿信号是相同的，故在有无同步系数情况下，其跟踪误差和同步误差都基本一致趋向于0。艏摇情况下，液压缸1，3，5；2，4，6 接收的位姿信号相同。纵荡、纵摇情况下，液压缸1，6，液压缸2，5，液压缸3，4接受的位姿信号相同。横荡、横摇情况下，六个液压缸接收到的位姿信号各不相同。在这六种情况下，不添加同步系数，仿真出跟踪误差基本趋向一致，都趋向于0，但同步误差相差较大，易使各通道间发生不协调运动。如图11～图13所示，由于各个位姿信号不相同，在引入同步系数的情况下，同步误差较小，且都能够一致趋向于0。如图14～图 17所示，在有扰动的情况下，各个液压缸具有较好的同步控制精度，在30s时，向液压缸一施加一个阶跃负载扰动，各个位姿情况下，液压缸一的同步误差变大，通过相邻交叉耦合的方式，与其相邻的液压缸二和液压缸六的同步误差变化明显，其余液压缸也会相应增大，使液压缸同步误差变化一致，最终能够平稳趋向于0。