基于牛顿插值公式及霍纳法则的大规模卫星轨道计算方法与流程

本申请涉及卫星定位，尤其涉及一种基于牛顿插值公式及霍纳法则的大规模卫星轨道计算方法、装置、电子设备及计算机可读存储介质。

背景技术：

1、卫星导航与定位系统在进行定位和导航时，需要用星历信息和历书信息，其中，星历可分为广播星历和精密星历，精密星历精度较高，主要用于事后处理，一般用于精密定位，往往需要延迟两周左右后才能获得；广播星历是根据卫星导航与定位系统控制中心跟踪站的观测数据进行外推处理后通过卫星播发的预报星历，主要用于实时导航定位。卫星导航定位实际上就是根据已知的卫星轨道信息和用户的观测资料，通过数据处理确定接收机的位置及其载体的航行速度。

2、其中，在卫星轨道坐标计算方面，可以根据广播星历计算出星历参数，进而求出卫星的空间坐标；还可以根据精密星历直接插值，得到卫星的轨道坐标。然而，广播星历的精度较低（一般为2m左右），计算出的卫星空间坐标的精度也较低，不适用于对导航精度需求较高的场合。另外，精密星历的精度很高，能够满足大部分场合的精度要求，但采用现有的轨道插值算法还存在诸多问题，例如，一是插值计算的时间复杂度高，计算量大，非常耗时，不适用于快速响应的场合；二是插值的拟合精度较差，存在较大的提升空间。

技术实现思路

1、有鉴于此，本申请实施例提供一种基于牛顿插值公式及霍纳法则的大规模卫星轨道计算方法、装置、电子设备及计算机可读存储介质，用于解决至少一种技术问题。

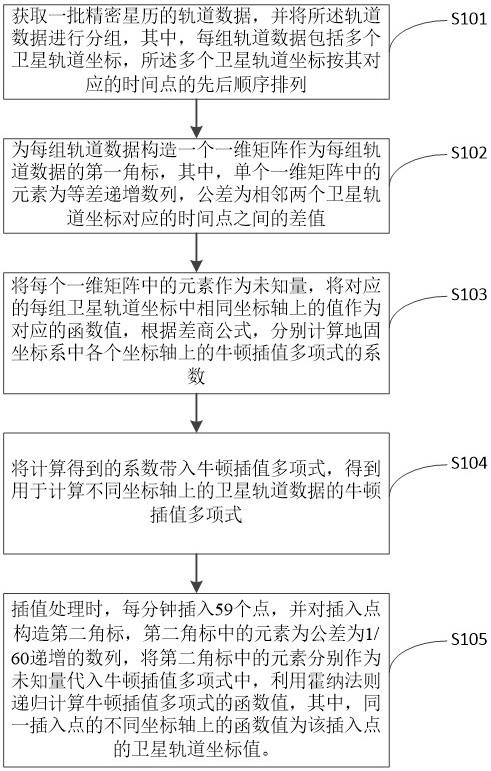
2、本申请实施例提供一种基于牛顿插值公式及霍纳法则的大规模卫星轨道计算方法，包括：获取一批精密星历的轨道数据，并将所述轨道数据进行分组，其中，每组轨道数据包括多个卫星轨道坐标，所述多个卫星轨道坐标按其对应的时间点的先后顺序排列；为每组轨道数据构造一个一维矩阵作为每组轨道数据的第一角标，其中，单个一维矩阵中的元素为等差递增数列，公差为相邻两个卫星轨道坐标对应的时间点之间的差值；将每个一维矩阵中的元素作为未知量，将对应的每组卫星轨道坐标中相同坐标轴上的值作为对应的函数值，根据差商公式，分别计算地固坐标系中各个坐标轴上的牛顿插值多项式的系数；将计算得到的系数带入牛顿插值多项式，得到用于计算不同坐标轴上的卫星轨道数据的牛顿插值多项式；插值处理时，每分钟插入59个点，并对插入点构造第二角标，第二角标中的元素为公差为1/60递增的数列，将第二角标中的元素分别作为未知量代入牛顿插值多项式中，利用霍纳法则递归计算牛顿插值多项式的函数值，其中，同一插入点的不同坐标轴上的函数值为该插入点的卫星轨道坐标值。

3、可选地，根据本申请实施例的方法，在将所述轨道数据进行分组时，以分钟为单位获取轨道数据，以6分钟为一组进行轨道数据的分组，每组轨道数据中包括6个分钟点对应的卫星轨道坐标。

4、可选地，根据本申请实施例的方法，所述第一角标对应的一维矩阵中的元素为1、2、3、4、5和6。

5、可选地，根据本申请实施例的方法，所述卫星轨道坐标为地固坐标系下的空间坐标，包括x、y、z三个不同坐标方向上的坐标值。

6、可选地，根据本申请实施例的方法，所述牛顿插值多项式为：

7、p(x)=a[0]+a[1](x-c[0])+a[2](x-c[0])(x-c[1])+...+a[n](x-c[0])(x-c[1])...(x-c[n-1]),其中，

8、a[0]=f(x0),

9、,

10、,

11、其中c矩阵中的元素为第一角标的一维矩阵中的元素，且不包含一维矩阵中的最后一个元素。

12、可选地，根据本申请实施例的方法，所述方法还包括：通过将计算得到的59个插值点的卫星轨道坐标与真实的卫星轨道数据进行比较，完成数据校验，和/或，确定利用牛顿插值多项式得到的卫星轨道坐标的精度。

13、本申请实施例提出一种基于牛顿插值公式及霍纳法则的大规模卫星轨道计算装置，包括：分组模块，获取一批精密星历的轨道数据，所述分组模块用于将所述轨道数据进行分组，其中，每组轨道数据包括多个卫星轨道坐标，所述多个卫星轨道坐标按其对应的时间点的先后顺序排列； 第一构造模块，用于为每组轨道数据构造一个一维矩阵作为每组轨道数据的第一角标，其中，单个一维矩阵中的元素为等差递增的数列，公差为相邻两个卫星轨道坐标对应的时间点之间的差值；系数计算模块，用于将每个一维矩阵中的元素作为未知量，将对应的每组卫星轨道坐标中相同坐标轴上的值作为对应的函数值，根据差商公式，分别计算地固坐标系中各个坐标轴上的牛顿插值多项式的系数；插值多项式计算模块，用于将计算得到的系数带入牛顿插值多项式中，得到用于计算不同坐标轴上的卫星轨道数据的牛顿插值多项式；第二构造模块，用于每分钟插入59个点，并对插入点构造第二角标，第二角标中的元素为公差为1/60递增的数列；坐标值计算模块，用于将第二角标中的元素分别作为未知量代入牛顿插值多项式中，利用霍纳法则递归计算牛顿插值多项式的函数值，其中，同一个插入点的不同坐标轴上的函数值为该插入点的卫星轨道坐标值。

14、本申请实施例提供一种电子设备，所述电子设备包括处理器以及存储有计算机程序指令的存储器；所述处理器执行所述计算机程序指令时实现如上所述的方法的步骤。

15、本申请实施例提供一种计算机可读存储介质，所述计算机可读存储介质上存储有计算机程序指令，所述计算机程序指令被处理器执行时实现如上所述的方法的步骤。

16、本申请实施例的基于牛顿插值公式及霍纳法则的大规模卫星轨道计算方法，在获取的精密星历的轨道数据的基础上，利用牛顿插值算法和霍纳法则算法实现卫星轨道坐标的快速计算，进而在面对大规模卫星轨道坐标计算时，相比于以往需要几分钟才能计算出结果，利用本申请可以在秒级的时间内计算出结果，满足高精度导航对于快速响应的要求；并且计算出的卫星轨道坐标能够高精度拟合真实的卫星轨道坐标，满足高精度导航和科学研究等领域的使用要求。

技术特征：

1.一种基于牛顿插值公式及霍纳法则的大规模卫星轨道计算方法，其特征在于，包括：

2.根据权利要求1所述的方法，其特征在于，在将所述轨道数据进行分组时，以分钟为单位获取轨道数据，以6分钟为一组进行轨道数据的分组，每组轨道数据中包括6个分钟点对应的卫星轨道坐标。

3.根据权利要求2所述的方法，其特征在于，所述第一角标对应的一维矩阵中的元素为1、2、3、4、5和6。

4.根据权利要求1所述的方法，其特征在于，所述卫星轨道坐标为地固坐标系下的空间坐标，包括x、y、z三个不同坐标方向上的坐标值。

5.根据权利要求1所述的方法，其特征在于，所述牛顿插值多项式为：

6.根据权利要求1所述的方法，其特征在于，所述方法还包括：

7.一种基于牛顿插值公式及霍纳法则的大规模卫星轨道计算装置，其特征在于，包括：

8.一种电子设备，其特征在于，所述电子设备包括：处理器以及存储有计算机程序指令的存储器；所述电子设备执行所述计算机程序指令时实现如权利要求1-6中任一项所述的方法。

9.一种计算机可读存储介质，其特征在于，所述计算机可读存储介质上存储有计算机程序指令，所述计算机程序指令被处理器执行时实现如权利要求1-6中任一项所述的方法。

技术总结
本申请公开了一种基于牛顿插值公式及霍纳法则的大规模卫星轨道计算方法。该方法包括：获取一批精密星历的轨道数据，并将所述轨道数据进行分组，其中，每组轨道数据包括多个卫星轨道坐标，所述多个卫星轨道坐标按其对应的时间点的先后顺序排列；为每组轨道数据构造一个一维矩阵作为每组轨道数据的第一角标，其中，单个一维矩阵中的元素为等差递增数列，公差为相邻两个卫星轨道坐标对应的时间点之间的差值。利用本申请实施例能够实现卫星轨道坐标的高精度拟合，提高卫星轨道坐标的计算速度。

技术研发人员：武军,王世金,赵志强,杨建冰
受保护的技术使用者：数字太空（北京）科技股份公司
技术研发日：
技术公布日：2024/1/14