基于混频信号与其一次积分信号的目标速度精确计算方法

本发明涉及目标精确测速，尤其涉及基于混频信号与其一次积分信号的目标速度精确计算方法。

背景技术：

1、在交通测速领域，连续波雷达具有设备简单、轻便、测速精度高以及无近距离盲区等优点，已广泛应用于车辆目标的速度测量。随着数字信号处理技术的发展，连续波雷达主要采用基于fft变换的数字比相方法进行测速，其测速精度与频谱估计有关，即频率分辨率。

2、雷达信号处理通常采用频谱估计。离散傅里叶变换(dft)作为经典频谱估计理论中的基本方法，最初用于计算雷达的混频以提取目标距离。随后，快速傅里叶变换(fft)的发展显著增强了dft在频域分析中的应用。然而，当存在固定的采样间隔和有限的长度时，频谱泄漏和栅栏效应严重影响了fft的频率估计精度，导致测距误差。为解决这些问题，众多研究专注于插值技术，即通过窗函数和插值来减少频谱泄漏和栅栏效应。尽管它们受到欢迎，但在频谱中存在相干信号时，插值方法的准确性较低。目前，频率估计方法主要分为时域和频域方法。时域方法包括最大似然(ml)算法、自回归(ar)谱估计方法、多信号分类(music)算法和旋转不变技术的信号参数估计(esprit)算法。上述方法各有优劣，如ml法计算复杂度较高；ar谱估计方法易受到噪声和异常值的影响；music算法处理相干信号源时存在限制，且计算复杂度高；esprit算法利在小样本量应用中存在局限性等。

3、相对而言，频域法因其计算量小且效率高更适合实时信号处理。其本质上利用fft变换和频率细化技术进行精确频率估计。频域方法主要包括振幅比法、邻近谱细化法、自相关法和谱线拟合法等。这些方法虽计算简单，但估计准确性低，并易受目标距离的影响。与基于fft的技术不同，基于矩阵的奇异值分解(svd)和奇异谱分解(ssd)旨在将信号表示为基本变量模态的线性组合，而不包含多余的谐波成分。尽管这些技术不提供频谱估计，但它们作为强大的去噪滤波器，能够分离自相关特征与随机特征。此外，小波变换(wt)和希尔伯特-黄变换(hht)常用于提取信号特征，但无法准确计算多频信号的频率。

4、为了实现混频信号的频率的精确计算，本方面从基本理论计算出发，提出一种基于混频信号与其一次积分信号的目标速度精确计算方法，可实现目标速度的精确求解。

技术实现思路

1、本发明的目的是提供基于混频信号与其一次积分信号的目标速度精确计算方法，不同于传统的频率估计法，该方法在解决fft变换存在的栏栅效应和频谱泄露的同时，不受频率分辨率的限制，采用了混频信号的积分信号，实现了目标速度的精确求解，具有抗噪性。

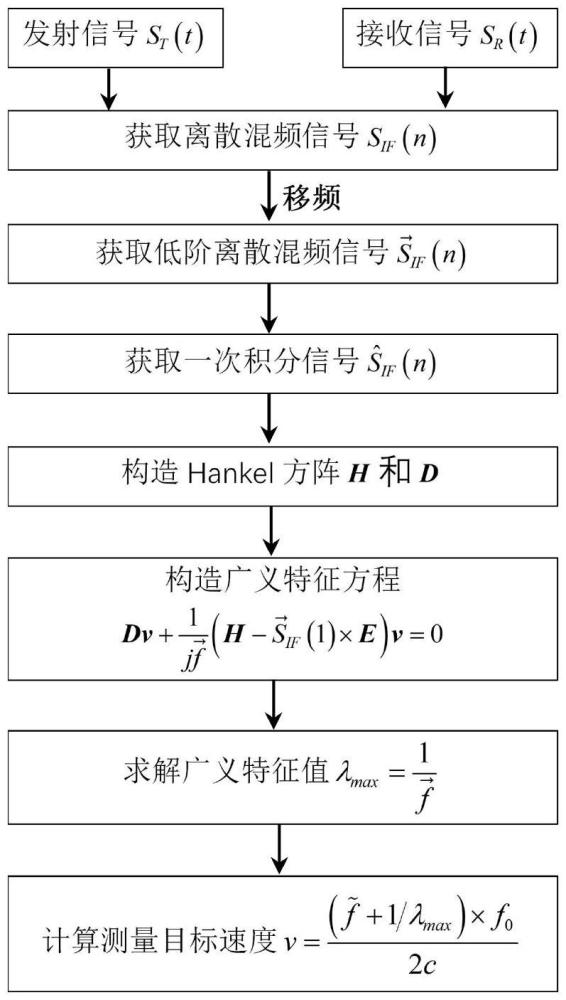
2、为实现上述目的，本发明提供了基于混频信号与其一次积分信号的目标速度精确计算方法，包括以下步骤：

3、步骤s1、获取离散混频信号；

4、步骤s2、获取移频后的低阶离散混频信号；

5、步骤s3、获取低阶离散混频信号的一次积分信号；

6、步骤s4、构造hankel方阵；

7、步骤s5、构造广义特征方程；

8、步骤s6、对广义特征方程进行求解。

9、优选的，在步骤s1中，获取离散混频信号，具体过程如下：

10、步骤s11、通过单频连续波雷达发射一个起始频率为f0，周期为tc，幅度为at,初始相位为的微波信号，如下所示：

11、

12、步骤s12、经速度为v的目标反射后被接收，得到接收信号，如下所示：

13、

14、其中，τ＝2vt/c为测量目标的时延，c＝3.0×108m/s为光速，k为回波衰减系数；

15、步骤s13、对接收和发射信号进行混频处理，并忽略信号幅度的影响，得到混频信号，如下所示：

16、

17、其中，为多普勒频率；

18、步骤s14、对上述混频信号进行数字ad离散采样，采样频率为fs，采样点数为n，得到离散采样后的混频信号，如下所示：

19、

20、优选的，在步骤s2中，获取移频后的低阶离散混频信号，具体过程如下：

21、步骤s21、对上述离散混频信号sif(n)进行n点fft变换，获得测目标的频谱信息；

22、步骤s22、选取被测目标频谱的峰值点fmax，以其左侧频谱点为参考频谱点，其中df＝1/tc；

23、步骤s23、构造参考信号，如下所示：

24、

25、步骤s24、根据参考信号对离散混频信号进行移频处理，得到低阶离散混频信号，如下所示：

26、

27、其中，

28、优选的，在步骤s3中，对上述低阶离散混频信号进行一次积分，得到一次积分信号，如下所示：

29、

30、优选的，在步骤s4中，根据上述低阶离散混频信号和其一次积分信号构造hankel方阵h和d，方阵h的第m行第l列，如下所示：

31、

32、优选的，在步骤s5中，根据上述hankel方阵h和d，建立广义特征方程，如下所示：

33、

34、其中，矩阵e为所有元素均为1的方阵。

35、优选的，在步骤s6中，对上述广义特征方程进行求解，得到特征值矩阵，选取其最大特征值并进行关系换算，得到被测目标的精确速度，如下所示：

36、

37、因此，本发明采用上述基于混频信号与其一次积分信号的目标速度精确计算方法，不同于传统的频率估计法，该方法在解决fft变换存在的栏栅效应和频谱泄露的同时，不受频率分辨率的限制，采用了混频信号的积分信号，实现了目标速度的精确求解，具有抗噪性。

38、下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。

技术特征：

1.基于混频信号与其一次积分信号的目标速度精确计算方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的基于混频信号与其一次积分信号的目标速度精确计算方法，其特征在于，在步骤s1中，获取离散混频信号，具体过程如下：

3.根据权利要求2所述的基于混频信号与其一次积分信号的目标速度精确计算方法，其特征在于，在步骤s2中，获取移频后的低阶离散混频信号，具体过程如下：

4.根据权利要求3所述的基于混频信号与其一次积分信号的目标速度精确计算方法，其特征在于，在步骤s3中，对上述低阶离散混频信号进行一次积分，得到一次积分信号，如下所示：

5.根据权利要求4所述的基于混频信号与其一次积分信号的目标速度精确计算方法，其特征在于，在步骤s4中，根据上述低阶离散混频信号和其一次积分信号构造hankel方阵h和d，方阵h的第m行第l列，如下所示：

6.根据权利要求5所述的基于混频信号与其一次积分信号的目标速度精确计算方法，其特征在于，在步骤s5中，根据上述hankel方阵h和d，建立广义特征方程，如下所示：

7.根据权利要求6所述的基于混频信号与其一次积分信号的目标速度精确计算方法，其特征在于，在步骤s6中，对上述广义特征方程进行求解，得到特征值矩阵，选取其最大特征值并进行关系换算，得到被测目标的精确速度，如下所示：

技术总结
本发明属于目标精确测速技术领域，公开了基于混频信号与其一次积分信号的目标速度精确计算方法，包括以下步骤：步骤S1、获取离散混频信号；步骤S2、获取移频后的低阶离散混频信号；步骤S3、获取低阶离散混频信号的一次积分信号；步骤S4、构造Hankel方阵；步骤S5、构造广义特征方程；步骤S6、对广义特征方程进行求解。本发明采用上述的基于混频信号与其一次积分信号的目标速度精确计算方法，不同于传统的频率估计法，该方法在解决FFT变换存在的栏栅效应和频谱泄露的同时，不受频率分辨率的限制，采用了混频信号的积分信号，实现了目标速度的精确求解，具有抗噪性。

技术研发人员：赵文举,黄璜,庞瑞,党隆基
受保护的技术使用者：河南工业大学
技术研发日：
技术公布日：2025/3/31