设计相位滞后校正环节的频域性能曲线图法的制作方法
技术领域:
本发明属于机械工程控制领域,特别涉及一种设计相位滞后校正环节的频域性能曲线图法。
背景技术:
:
如受控机械系统的控制性能(稳定性、准确性和快速性)不满足要求,则可通过在系统中增加校正环节的方法,以改善受控机械系统的控制性能。相位滞后校正是常用的校正方法之一。
在机械工程控制领域,设计相位滞后校正环节最为常用的方法为应用伯德图进行设计的频域设计方法。该方法一般以相位裕度为性能指标,借助伯德图通过解析计算确定校正环节参数。该方法满足给定的相位裕度要求,是可行解,但不是最优解。另外,对系统控制性能评价的频域性能指标不仅仅是相位裕度,还有剪切频率、截止频率、谐振峰值、幅值裕度等;在初步设计的基础上需要验算其它性能指标是否也满足要求,如不满足,需要多次反复设计和验算,直到满足所有性能指标要求为至,繁琐而费时。
因对控制系统的性能有多方面的要求,多个控制性能指标间是相互矛盾的;校正环节参数对系统控制性能的影响也是相互矛盾的。因此,校正环节的参数设计是一个非常重要又非常困难的问题。
技术实现要素:
:
本发明针对现有技术中的不足,提出一种设计相位滞后校正环节的频域性能曲线图法,其具有直观、系统和全面的特点。
本发明解决其技术问题所采用的方案是:一种设计相位滞后校正环节的频域性能曲线图法,以相位滞后校正环节的两个控制参数分别为纵横坐标,建立一个有界的二维参数设计空间。以频域控制性能指标为目标函数,以相位滞后校正环节的两个控制参数为设计变量,在参数设计空间内绘制各个控制性能指标的等值线,可得到系统的控制性能曲线图。控制性能曲线图呈现了控制性能指标与校正环节参数之间的一一对应关系。协调和对比各个性能曲线图,则可得到控制性能综合最优的的校正环节参数,完成校正环节的最优化设计。
附图说明:
图1为系统传递函数方框图。
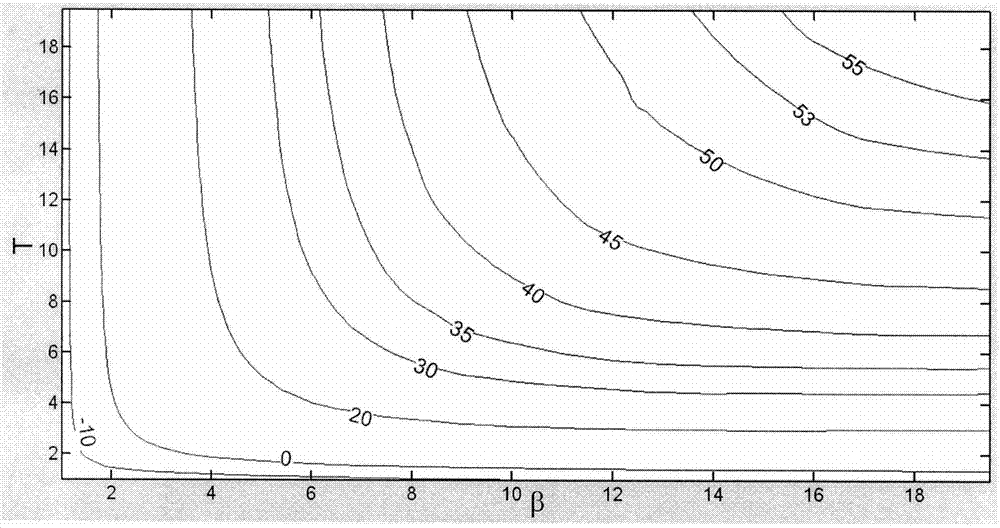
图2为相位裕度性能曲线图。
图3为剪切频率性能曲线图。
图4为谐振峰值性能曲线图。
图5为截止频率性能曲线图。
图6为单位阶跃响应曲线图。
具体实施方式:
以下结合附图和实施例对本发明作进一步详述:
如图1所示为系统传递函数方框图,相位滞后校正环节的传递函数为
分别以有界的控制参数t和β为纵横坐标,则可得校正环节的参数设计空间。以频域控制性能指标为目标函数,以参数t和β为设计变量,在参数设计空间中绘制目标函数等值线,则可得到各个性能指标的性能曲线图。
图2所示为相位裕度性能曲线图、图3所示为剪切频率性能曲线图、图4所示为谐振峰值性能曲线图、图5所示为截止频率性能曲线图。协调和对比各个性能曲线图,则可得到综合性能最优的校正环节参数。例如,这里可选择校正环节的参数为t=8和β=12.5。
图6所示为系统的单位阶跃响应曲线图,所述图6中三个子图分别对应为校正环节参数为t=0和β=0(无校正环节)时系统的单位阶跃响应曲线;校正环节参数为t=10和β=10(为满足相位裕度大于等于40°,应用基于伯德图的频域响应设计方法得到的校正环节参数)时系统的单位阶跃响应曲线;校正环节参数为t=12.5和β=8(应用所述频域性能曲线图法得到的校正环节参数)时系统的单位阶跃响应曲线。对比图6所示三个子图可见,频域性能曲线图法可显著改善系统的控制性能,并具有直观、系统、全面的特点。
技术特征:
技术总结
一种设计相位滞后校正环节的频域性能曲线图法,其特征是以相位滞后校正环节的两个控制参数分别为纵横坐标,建立一个有界的二维参数设计空间;以频域控制性能指标为目标函数,以相位滞后校正环节的两个控制参数为设计变量,在参数设计空间内绘制各个控制性能指标的等值线,得到系统的控制性能曲线图;控制性能曲线图呈现了控制性能指标与校正环节参数之间的一一对应关系;协调和对比各个性能曲线图,可得到控制性能综合最优的校正环节参数,完成校正环节的最优化设计。本发明具有直观、系统和全面的特点。
技术研发人员:王冰;高永亮
受保护的技术使用者:北华航天工业学院
技术研发日:2017.04.12
技术公布日:2017.07.04
- 还没有人留言评论。精彩留言会获得点赞!