一种受扰机械臂系统轨迹跟踪优化控制方法及存储介质与流程

本发明涉及机械臂轨迹跟踪优化，具体涉及一种受扰机械臂系统轨迹跟踪优化控制方法及存储介质。

背景技术：

1、机械臂通常是通过各关节连接成的运动链组成，凭借其集成度高、灵活性强等特点，常见于各种高端应用场景，如智能制造、航空航天和医疗手术中。在这类应用中，机械臂通常用于配合完成更精准、高效的工程任务，因此对机械臂的高精度轨迹跟踪提出了更迫切的性能要求。然而，在实际工业场景中，较为常见的仍是基于串级pid的控制方法，用以完成各种复杂的工况任务。然而，机械臂系统本质上是一个具有强耦合性且包含复杂不确定性的非线性控制对象，仅利用pid可能难以达成较好的控制期望，甚至会发生工业事故。因此，研究针对机械臂的先进控制算法具有较高的现实意义。

2、现有的诸多控制方案已用于机械臂轨迹跟踪控制，其大体可归结为如下几种：鲁棒控制、模型预测控制(model predictive control, mpc)、自适应神经网络控制和滑模控制等。其中，mpc得益于其实现简单，轨迹跟踪控制性能高，一直被研究者认为是极具开发前景的控制策略，因而近年来受到了工程从业人员广泛的关注。通常，mpc策略可被细分为离散时间优化控制及连续时间优化控制。前者通常凭借其可以兼顾优化以解决系统内部的状态约束而广受应用，但其控制效果受到采样控制周期的很大影响，且一味地追求控制性能，会进一步造成计算负担过大的问题，进而破坏控制系统的实时性。为了缓解这个问题，yang提出一种广义预测控制(generalized predictive control, gpc)策略，这种方法无需对模型做离散化处理，而是直接用系统动力学模型的泰勒近似值进行优化性能指标的运算，从而获取最终的显示解析解，具有设计过程简洁，计算量更小且有明确的参数整定机制等优点。

3、然而，由机械臂系统建模的参数摄动，未建模的高阶动力学状态，系统所受外部干扰等组成的集总不确定性普遍存在于各类工程对象中，其负面作用势必会造成控制性能的下降，甚至出现安全问题，即完成既定的对于含不确定性的机械臂系统的高精度的轨迹跟踪控制是具有一定难度的。同样，不确定性的存在也给传统的mpc设计带来了较大的挑战。为此，在控制器设计过程中需要将系统所受的不确定性考虑在内，从而提高闭环系统的各项性能。

技术实现思路

1、本发明的目的是针对现有技术存在的不足，提供一种受扰机械臂系统轨迹跟踪优化控制方法及存储介质。

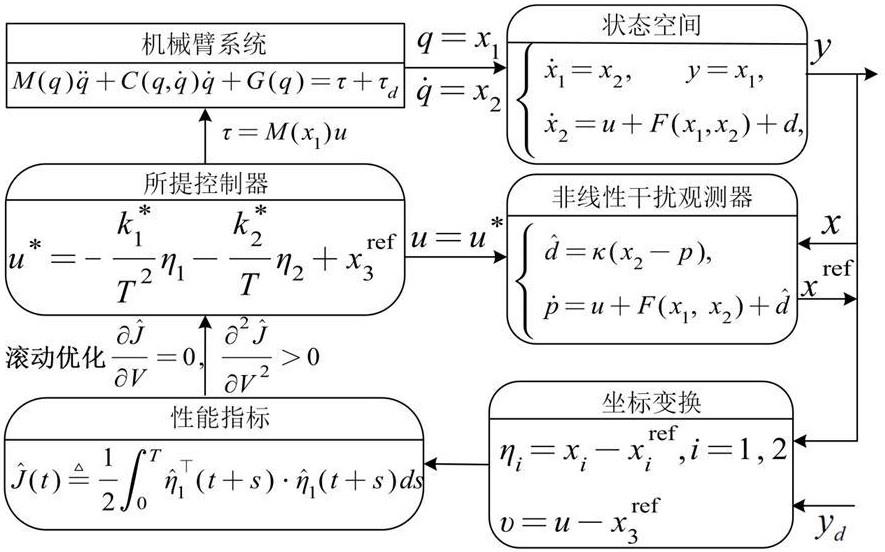
2、为实现上述目的，在第一方面，本发明提供了一种受扰机械臂系统轨迹跟踪优化控制方法，包括：

3、步骤1、对由n个连杆组成的机械臂系统构建动态模型，并将所述动态模型转化为空间状态形式；

4、步骤2、设计干扰观测器，以对机械臂系统中所含的不确定性进行估计；

5、步骤3、通过系统化地前馈补偿设计修正系统的稳态信号，从而得到经过动态补偿的预测模型；

6、步骤4、基于所述经过动态补偿的预测模型获得标称系统模型，并利用所得的标称系统模型进行广义预测控制中的滚动优化运算，并通过求解与关节角度跟随误差相关的性能指标优化函数，得出广义预测控制器的预测控制律。

7、进一步的，所述动态模型被描述为：

8、

9、其中，分别是关节角度、角速度和加速度矢量，，为n维实数集，为关节扭矩，，为惯性矩阵，，并且，为向心力和科里奥利力矩阵，为机械臂的重力项，，为系统的参数化不确定性、未建模动态和外部干扰的集总扰动。

10、进一步的，将所述动态模型转化为空间状态形式的方式具体如下：

11、定义和，将机械臂系统重新描述为如下状态空间形式：

12、

13、其中，、分别为和的一阶导数，为预测控制律，为集总干扰，为系统已知动态模型；

14、

15、。

16、进一步的，所述干扰观测器表示为：

17、

18、其中，为干扰观测器的内部辅助状态，为的一阶导数，为待设计的正定增益矩阵，为的估计向量；

19、定义干扰观测器的估计误差，得到干扰观测器的误差方程满足：

20、

21、其中，为的一阶导数。

22、进一步的，所述步骤3具体包括：

23、基于干扰观测器估计值，并通过修正系统中未知的不确定项，得到稳态参考信号、、：

24、

25、

26、其中，为机械臂系统期望的给定轨迹，为的一阶导数，为的二阶导数，为系统已知动态模型在稳态参考信号、处的数值；

27、然后做如下的坐标转换：

28、

29、建立以为新状态变量的非线性系统，具体如下：

30、

31、

32、其中，表示矩阵的转置，为n阶单位矩阵，为的一阶导数。

33、进一步的，所述步骤4具体包括：

34、设定如下优化性能指标：

35、

36、其中，为预测周期，为时间变量，为积分中间变量；

37、通过忽略所述非线性系统中的估计误差及非线性跟踪误差项，得到标称系统模型为：

38、

39、将跟踪偏差在一次预测周期[0,t]内沿着标称系统利用泰勒级数展开近似得到：

40、

41、

42、其中，为阶乘符号，为标称系统的控制阶数；

43、所述优化性能指标进一步计算为：

44、

45、

46、

47、

48、对沿着求偏导运算，并取，，同时在已知非奇异的前提下，计算得到预测控制律为：

49、。

50、进一步的，将的第一列作为最优预测控制律，由此可进一步得到：

51、

52、。

53、进一步的，将所述控制阶数选为0，并将所述最优控制律进行简化，简化后的最优控制律为：

54、

55、其中，分别为与,有关的常值矩阵，。

56、在第二方面，本发明提供了一种存储介质，存储有计算机程序，所述计算机程序被处理器执行时实现上述的方法。

57、有益效果：本发明采用干扰观测器在线重构机械臂系统的不确定性模型，并随之设计补偿回路，修正不确定系统的未知信息，然后利用不确定性估计信息对预测控制的标称模型做优化，根据设定的含关节跟踪误差的性能指标，计算得出广义预测控制律的显式形式，本发明相比于传统逆动力学控制策略，在轨迹跟踪精度和抗干扰能力方面皆具有明显的优势，具有更准确的关节位置响应和更强的闭环鲁棒性能。

技术特征：

1.一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，包括：

2.根据权利要求1所述的一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，所述动态模型被描述为：

3.根据权利要求2所述的一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，将所述动态模型转化为空间状态形式的方式具体如下：

4.根据权利要求3所述的一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，所述干扰观测器表示为：

5.根据权利要求4所述的一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，所述步骤3具体包括：

6.根据权利要求5所述的一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，所述步骤4具体包括：

7.根据权利要求6所述的一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，将的第一列作为最优预测控制律，由此可进一步得到：

8.根据权利要求7所述的一种受扰机械臂系统轨迹跟踪优化控制方法，其特征在于，将所述控制阶数选为0，并将所述最优控制律进行简化，简化后的最优控制律为：

9.一种存储介质，存储有计算机程序，其特征在于，所述计算机程序被处理器执行时实现权利要求1-8任一项所述的方法。

技术总结
本发明公开了一种受扰机械臂系统轨迹跟踪优化控制方法及存储介质。该方法包括对由n个连杆组成的机械臂系统构建动态模型，并将所述动态模型转化为空间状态形式；设计干扰观测器，以对机械臂系统中所含的不确定性进行估计；通过系统化地前馈补偿设计修正系统的稳态信号，从而得到经过动态补偿的预测模型；基于经过动态补偿的预测模型获得标称系统模型，并利用所得的标称系统模型进行广义预测控制中的滚动优化运算，并通过求解与关节角度跟随误差相关的性能指标优化函数，得出广义预测控制器的预测控制律。本发明相比于传统逆动力学控制策略，在轨迹跟踪精度和抗干扰能力方面皆具有明显的优势，具有更准确的关节位置响应和更强的闭环鲁棒性能。

技术研发人员：杨民强,徐恒吉,陈鹏,陈建福,张哲,陈功,冒建亮,舒计城,郭守志,郭建豪,刘辉,孙小玉,杨靖科
受保护的技术使用者：中铁十四局集团大盾构工程有限公司
技术研发日：
技术公布日：2024/1/14