一种基于指数近似的可变精度浮点函数实现方法

1.本发明属于浮点数值计算领域，尤其涉及一种基于指数近似的可变精度浮点函数实现方法。


背景技术：

2.浮点函数是高性能应用中必不可少的重要组成，一般通过调用标准数学函数库实现，例如，linux gnu c数学函数库、python语言的数学模块等。这些标准数学函数库作为软件系统的重要组成部分，是影响高性能计算精度和运行性能的关键因素之一。尤其在生物医药、航空航天、国防军工等计算密集型应用领域，标准数学函数计算耗时占据相当大的比例。
3.在标准数学库的设计过程中，为了适用尽可能多的应用场景，浮点函数的实现一般会覆盖函数定义域的全部区间，并且尽可能地逼近当前浮点数类型的精度上限，以保证浮点函数在使用过程中不会出现准确性问题。
4.与传统的高精度计算相比，人工智能应用负载往往并不需要高精度，并且在模型推理场景中的精度要求比模型训练更低。因此，在ieee754双精度浮点数(fp64)和单精度浮点数(fp32)之外，英伟达公司提出了半精度浮点数(fp16)。人工智能研究人员可以借助英伟达张量核(tensor cores)，通过设定混合或匹配不同级别的精度方式进行运算，从而优化计算资源，加速人工智能应用。
5.本发明针对人工智能应用负载对浮点运算误差具有一定容忍度的特点，从优化指数类浮点函数计算方法角度出发，充分结合ieee754浮点数表示形式特点，采用“空间交换时间”的思想，提出了一种基于指数近似的可变精度浮点函数实现方法，通过降低一定浮点运算精度从而有效提升人工智能应用负载的计算性能。


技术实现要素：

6.本发明的目的在于针对现有技术的不足，提供一种基于指数近似的可变精度浮点函数实现方法。
7.本发明的目的是通过以下技术方案来实现的：一种基于指数近似的可变精度浮点函数实现方法，包括以下步骤：
8.(1)将人工智能应用负载中高频调用的浮点函数转换为以2为底数的表达式。
9.(2)根据步骤(1)得到的表达式，对该表达式的指数部分进行仿射变换得到中间变量。
10.(3)根据步骤(2)得到的中间变量，用该中间变量的部分低位比特作为索引检索查找表。
11.(4)使用步骤(3)中查找表的返回结果作为最终返回值的尾数域。
12.进一步地，所述步骤(1)中提及的人工智能应用负载具体为包含神经网络模型的应用。
13.进一步地，所述步骤(2)中提及的仿射变换具体为先加上相应浮点数类型的指数域偏移值再乘以2m，m与浮点数类型相关。该仿射变换保证了该中间变量的高位比特等于最终返回值的指数域，并且低位比特与最终返回值的尾数域存在对应关系。
14.进一步地，所述步骤(3)中的查找表具体为预先计算的以中间变量高位比特为索引(index)，待求解表达式精确结果的尾数域为值(value)的查找表。
15.进一步地，通过该方法实现的可变精度浮点函数通过控制查找表规模(索引长度)控制浮点函数的计算精度。
16.本发明的有益效果是：本发明能够用于实现一系列可变精度浮点函数，在保证精度在10-5
级别的前提下，运行速度最高为gnu发布的标准数学库的6.3倍。
附图说明
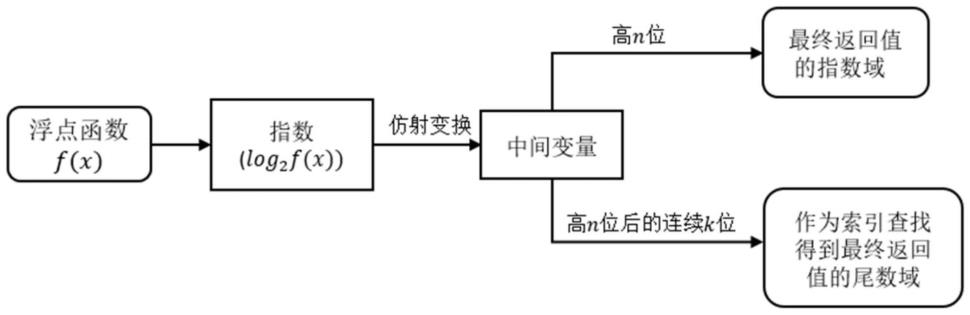
17.图1是基于指数近似的可变精度浮点函数的实现过程示意图。
18.图2是当数据类型为双精度浮点数时的仿射变换示意图。
具体实施方式
19.一种基于指数近似的可变精度浮点函数实现方法，如图1所示，包括以下步骤：
20.1、将待求解浮点函数转换为以2为底数的表达式。
21.2、根据步骤1得到的表达式，对该表达式的指数部分进行仿射变换得到中间变量。
22.步骤2中提及的仿射变换具体为先加上相应浮点数类型的指数域偏移值再乘以2m，m与浮点数类型相关。该仿射变换保证了该中间变量的高位比特等于最终返回值的指数域，并且低位比特与最终返回值的尾数域存在对应关系。以双精度浮点数类型(固定偏移值为1023)为例，当指数部分为6.1352时，首先做加上固定偏移值1023再乘以2
20
的仿射变换，再对其取整。其最终结果的二进制形式如图2所示。
23.3、根据步骤2得到的中间变量，取其高n位作为返回值的指数域，n为对应浮点数类型的指数域长度。取中间变量的高n位后的连续k位比特作为索引检索查找表，k为索引长度。
24.步骤3中的查找表具体为预先计算的以中间变量高位比特为索引(index)，待求解表达式精确结果的尾数域为值(value)的查找表。
25.4、使用步骤3中查找表的返回结果作为最终返回值的尾数域。
26.该方法实现的可变精度浮点函数通过控制查找表规模(索引长度)控制浮点函数的计算精度。


技术特征：
1.一种基于指数近似的可变精度浮点函数实现方法，其特征在于，包括以下步骤：(1)将人工智能应用负载中高频调用的浮点函数转换为以2为底数的表达式；(2)根据步骤(1)得到的表达式，对该表达式的指数部分进行仿射变换得到中间变量；(3)根据步骤(2)得到的中间变量，取其高n位作为返回值的指数域，n为对应浮点数类型的指数域长度，取中间变量的高n位后的连续k位比特作为索引检索查找表，k为索引长度；(4)使用步骤(3)中查找表的返回结果作为最终返回值的尾数域。2.根据权利要求1所述基于指数近似的可变精度浮点函数实现方法，其特征在于，所述步骤(1)中的人工智能应用负载具体为包含神经网络模型的应用。3.根据权利要求1所述基于指数近似的可变精度浮点函数实现方法，其特征在于，所述步骤(2)中的仿射变换具体为先加上ieee 754标准规定的相应浮点数类型的指数域偏移值再乘以2
m
，m与浮点数类型相关；该仿射变换保证了该中间变量的高位比特等于最终返回值的指数域，并且低位比特与最终返回值的尾数域存在对应关系。4.根据权利要求1所述基于指数近似的可变精度浮点函数实现方法，其特征在于，所述步骤(3)中的查找表具体为预先计算的以中间变量高位比特为索引，待求解表达式精确结果的尾数域为值的查找表。5.一种基于指数近似的可变精度浮点函数实现方法，其特征在于，通过控制查找表规模(索引长度)控制浮点函数的计算精度。

技术总结
本发明公开了一种基于指数近似的可变精度浮点函数实现方法，该方法结合了IEEE 754浮点数表示形式特点和“空间交换时间”的思想。首先，将人工智能应用负载中高频调用的待求解的浮点函数转换为以2为底数的表达式。接着，对表达式的指数进行仿射变换(先平移后放缩)得到中间变量。最后，用中间变量的低位比特作为索引检索查找表，并用返回结果作为最终返回值的尾数域。该方法通过改变查找表规模控制浮点函数的计算精度。使用本发明可以实现一系列可变精度的浮点函数，具有较好的应用前景。具有较好的应用前景。具有较好的应用前景。


技术研发人员：张青锖 蔡铭
受保护的技术使用者：浙江大学
技术研发日：2022.03.25
技术公布日：2022/7/8