复杂耦合工程系统的快变-慢变融合稳定性分析方法

1.本发明涉及复杂工程系统耦合振动领域，特别是涉及一种复杂耦合工程系统的快变-慢变融合稳定性分析方法。


背景技术：

2.工程中复杂耦合振动系统大多具有非线性特征，对于其动力学模型的求解大多数采用近似或者忽略非线性因素的方法对系统进行近似分析。然而随着工程对系统稳定性要求的日益提高，传统的计算方式并不能保证足够小的误差，甚至对系统的稳定性做出错误判断。
3.为了解决上述问题，本发明提出了一种复杂耦合工程系统的快变-慢变融合稳定性分析方法，该方法将系统的响应视为多个时间标度下响应的叠加，从而求解出不同时间标度下的系统的幅值和频率变化，即系统的快变与慢变，从而对系统稳定性进行分析；填补国际相关技术空白，推动工程技术发展，又可产生较大的社会效益与经济效益。


技术实现要素：

4.为了克服现有技术不足，填补相关技术空白，本发明提供了一种复杂耦合工程系统的快变-慢变融合稳定性分析方法，该方法通过引入不同的时间标度，将系统的响应视为不同阶数响应的叠加，从而将系统振动微分方程转化为关于多个时间标度的偏微分方程组，求解不同时间标度下系统振幅和频率变化，即系统响应的快变与慢变，得出系统幅频响应，对系统稳定性进行分析。
5.本发明解决其技术问题所采用的技术方案如下：一种复杂耦合工程系统的快变-慢变融合稳定性分析方法，其特征在于：步骤(1)：对于非线性复杂系统，以振动位移及其一阶导数为变量，建立其振动微分方程的一般形式为：，其中f函数中包含x的非线性运算，对于不同的系统参数和f运算，系统的响应可描述成多种不同时间周期响应的叠加，即快变与慢变的融合；步骤(2)：引入不同时间标度的变量，其中的绝对值远小于1，将系统的响应描述为多个时间标度的函数；其中，m为所计算的最高阶数，决定响应的计算精度；将时间标度视为各自独立，那么系统关于t的振动微分方程可视为关于m个时间标度的偏微分方程；步骤(3)：引入偏导算子，将系统中关于t的微分描述为关于时间标度的偏微分，，；步骤(4)：将系统响应和时间标度的偏微分代入振动微分方程，令的同次系数相等，可得到m阶偏微分方程组；所述振动微分方程需要小参数化为的同阶量，，以获取有
效的近似解；步骤(5)：将的i-1次偏微分方程的解代入的第i次方程求解，直到第m阶响应；对第i时间标度的偏微分方程求解，系统的振动响应写为共轭复指数形式，其中，，a描述了系统不同时间标度下的响应幅值，b描述了不同时间标度下的响应频率；对第i时间标度的偏微分方程求解时，为了提取出不同时间标度下系统的响应，应消去系统中频率与固有频率相等的永年项；若系统中涉及到固有频率w0的弦函数，则需引入失调量s，使w=w0+s，并用欧拉公式将弦函数转换为复指数函数。
6.与现有技术相比，本发明的有益效果：通过引入多个时间标度，将工程系统关于时间的振动微分方程转化为关于多个时间标度的偏微分方程组，进而求解出系统在不同时间标度下的振幅和频率响应，即系统的快变-慢变，对系统稳定性进行分析，大大提高复杂工程系统稳定性计算精度和判定准确率。
附图说明
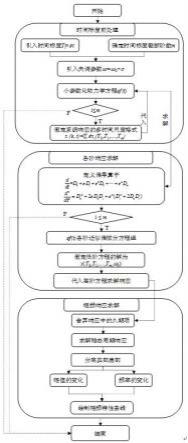
7.图1是复杂耦合工程系统的快变-慢变融合稳定性分析方法流程图；图2是车桥振动非线性系统以啮合阻尼为参数的幅频特性曲线族；图3是车桥振动非线性系统以啮合刚度波动为参数的幅频特性曲线族；图4是车桥振动非线性系统以载荷波动为参数的幅频特性曲线族。
具体实施方式
8.以复杂耦合工程系统中典型的车桥振动系统非线性动力学模型为例对本发明具体实施方式进行详细说明。
9.工程中常用的车桥耦合振动系统非线性动力学模型一般形式为：，本例中，，，，，；由于间隙f(x)的存在，该系统为典型复杂非线性动力系统，对其进行快变-慢变融合稳定性分析，参照图1所示为复杂耦合工程系统的快变-慢变融合稳定性分析方法流程图，包括以下步骤：步骤（1）：对f(x)进行立方项拟合，；步骤（2）：引入不同时间标度的变量，其中e=0.1，将系统的响应描述为多个时间标度的函数；其中，m为所计算的最高阶数，本案例中，m=2；步骤（3）：引入偏导算子，将系统中关于t的微分描述为关于时间标度
的偏微分，，；步骤（4）：将系统中的参数小参数化为、、、、，将啮合频率w写为。将近似解和偏导算子代入小参数化后的振动微分方程，展开后取到e的m次项，令e的同次幂系数相等，可得到各阶近似的偏微分方程组：；步骤（5）：假设e的0阶系数方程的解为：，其中，和互为共轭复数；步骤（6）：引入失调参数s，使w=w0+s，并改写方程中含激励频率的余弦函数：。将e的0阶系数方程的解和代入e的一阶系数偏微分方程，消去永年项后得到；步骤（7）：将a改写为系统不同时间标度下振幅a和频率b耦合变化的形式，代入消去永年项后的e一阶系数偏微分方程，分离实部和虚部后得到：；由此系统的幅频响应方程可以写为：；图2为车桥振动非线性系统以啮合阻尼为参数的幅频特性曲线族，根据非线性系统幅频响应方程得到以啮合阻尼为参数的w-a幅频特性曲线族，当啮合阻尼增加时，系统的振幅明显降低，且右侧不稳定弯曲分支缩减，说明适当增加阻尼有益于系统稳定；图3为车桥振动非线性系统以啮合刚度波动为参数的幅频特性曲线族，以啮合刚度波动为参数的w-a幅频特性曲线族，可以看出随着啮合刚度波动的增加，系统振幅逐渐降低且不稳定弯曲分支逐渐缩减直至消失；图4为车桥振动非线性系统以载荷波动为参数的幅频特性曲线族，以载荷波动f为参数的w-a幅频特性曲线族，载荷波动增加时，系统振幅升高且且右侧不稳定弯曲分支增长，系统稳定性变差。
10.以上所述，仅是发明的较佳实施方式，并非对本发明做任何限制，凡是根据本发明实质对以上实施方式所作的任何修改、变更以及等效变化，均仍属于本发明技术的保护范围之内。


技术特征：
1.一种复杂耦合工程系统的快变-慢变融合稳定性分析方法，其特征在于：步骤(1)：对于非线性复杂系统，以振动位移及其一阶导数为变量，建立其振动微分方程的一般形式为：，其中f函数中包含x的非线性运算，对于不同的系统参数和f运算，系统的响应可描述成多种不同时间周期响应的叠加，即快变与慢变的融合；步骤(2)：引入不同时间标度的变量，其中的绝对值远小于1，将系统的响应描述为多个时间标度的函数；其中，m为所计算的最高阶数，决定响应的计算精度；将时间标度视为各自独立，那么系统关于t的振动微分方程可视为关于m个时间标度的偏微分方程；步骤(3)：引入偏导算子，将系统中关于t的微分描述为关于时间标度的偏微分，，；步骤(4)：将系统响应和时间标度的偏微分代入振动微分方程，令的同次系数相等，可得到m阶偏微分方程组；所述振动微分方程需要小参数化为的同阶量，，以获取有效的近似解；步骤(5)：将的i-1次偏微分方程的解代入的第i次方程求解，直到第m阶响应；对第i时间标度的偏微分方程求解，系统的振动响应写为共轭复指数形式，其中，，a描述了系统不同时间标度下的响应幅值，b描述了不同时间标度下的响应频率；对第i时间标度的偏微分方程求解时，为了提取出不同时间标度下系统的响应，应消去系统中频率与固有频率相等的永年项；若系统中涉及到固有频率w0的弦函数，则需引入失调量s，使w=w0+s，并用欧拉公式将弦函数转换为复指数函数。

技术总结
本发明公开了一种复杂耦合工程系统的快变-慢变融合稳定性分析方法，其包括以下步骤：（1）建立工程系统的非线性振动微分方程；（2）引入不同时间标度的变量，将系统的响应假设为多个时间标度下不同响应的叠加；（3）定义偏导算子，将系统关于时间的微分转换为关于时间标度的偏微分，将系统的微分方程转化为关于多个时间标度的偏微分方程；（4）将系统响应和时间标度的偏微分代入振动微分方程，得到偏微分方程组；（5）依次求解各阶偏微分方程，得到系统不同时间标度下的响应，即系统的快变-慢变；有益效果是该方法能够准确反映出复杂耦合工程系统的快变-慢变融合，并对系统稳定性进行分析。并对系统稳定性进行分析。并对系统稳定性进行分析。


技术研发人员：莫帅 张应新
受保护的技术使用者：广西大学
技术研发日：2022.05.13
技术公布日：2022/7/28