一种用于提升分子动力学模拟核磁共振弛豫尺度的方法

本发明属于多孔介质核磁共振弛豫，特别涉及一种用于提升分子动力学模拟核磁共振弛豫尺度的方法。

背景技术：

1、核磁共振弛豫技术(nmr)利用弛豫时间可以获得多孔介质的孔隙度、渗透率、孔径分布等表征孔隙的特征参数，还能观测、分析流体分子的动力学行为。因此，人们常借助核磁共振弛豫模拟手段，获得多孔介质的核磁共振响应，提取孔隙信息。最常用的是蒙特卡洛随机游走方法，该方法将扩散分子视为传播子，计算传播子的运动轨迹。但是，蒙特卡洛随机游走方法统计的为平均陨灭概率，是一种唯象理论。该方法无法处理粒子之间的相互作用，难以对多孔介质表面吸附、解析附直接进行响应。因此有必要将nmr模拟从传统的蒙特卡洛模拟中升级到考虑分子相互作用，以及粒子碰撞的方法中来。

2、随着计算机计算能力的增强和力场模型的完善，分子动力学(md)模拟成为研究蛋白质、聚合物、原油等大分子结构和分子动力学的有力工具。md模拟能够将核磁共振弛豫涉及的分子内氢核偶极-偶极相互作用和分子间偶极-偶极相互作用区分开来，从分子相互作用的角度解释复杂组分流体和多孔介质表面的核磁共振弛豫机理。该方法已经成功运用在了原油和干酪根的t1和t2弛豫机制解释上。但是，md模拟结果得到的等效t1和t2只能代表纳米(nm)尺度边界空间内的nmr特性，演化时间是皮秒(ps)级别。而常规nmr测量不能被如此小尺度的特性所模拟。因此，如何将md模拟结果提升到nmr测量尺度上，使得nmr的数值模拟可以同时考虑到分子级别和孔隙级别的各种参数的改变，成为是一个重要问题。

技术实现思路

1、针对现有技术中存在的问题，本发明公开了一种用于提升分子动力学模拟核磁共振弛豫尺度的方法，以解决分子动力学模拟核磁共振弛豫结果在应用上的尺度匹配问题。

2、本发明的上述技术目的是通过以下技术方案得以实现的：

3、一种用于提升分子动力学模拟核磁共振弛豫尺度的方法，具体步骤如下：

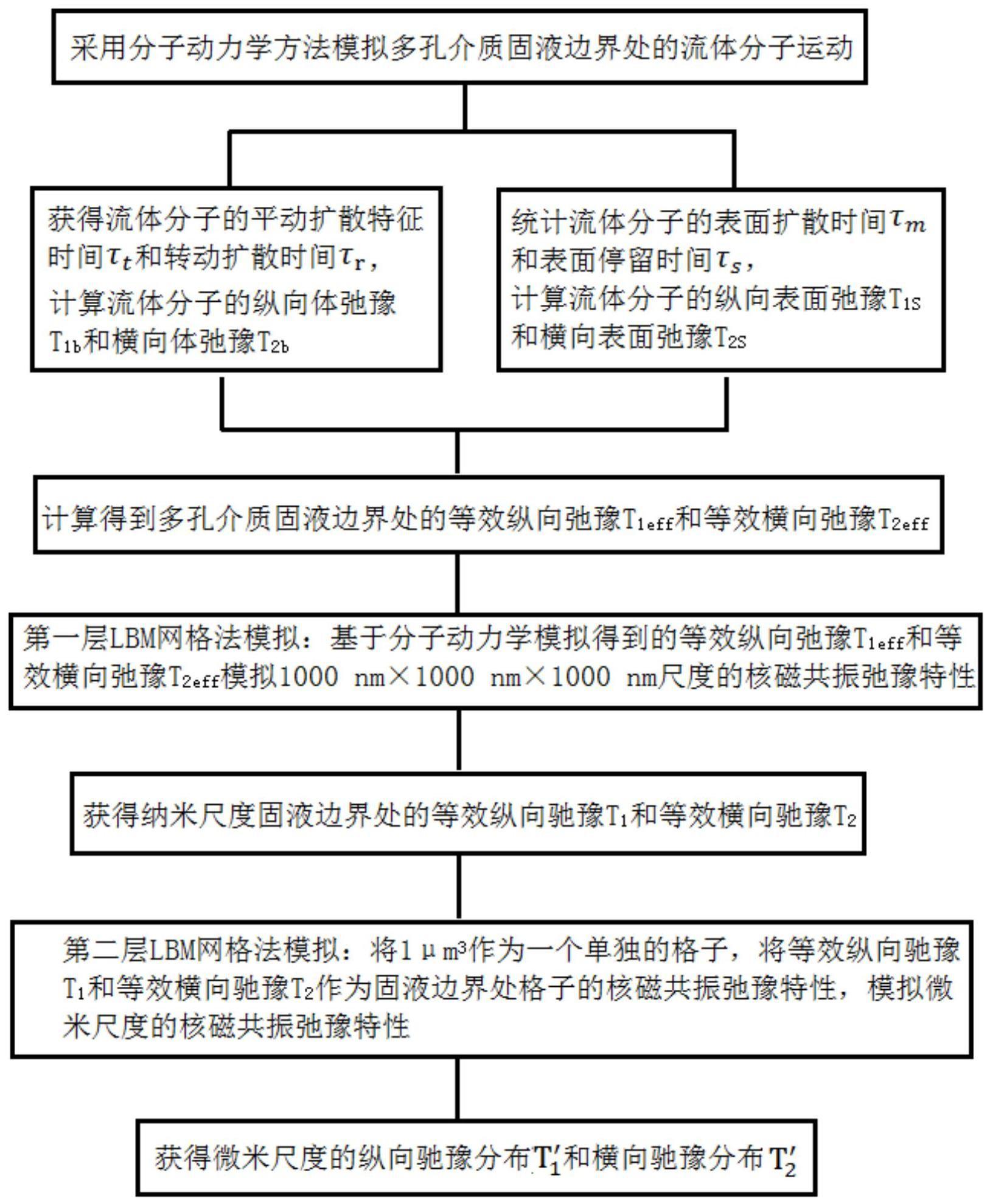
4、s1：采用分子动力学方法模拟多孔介质固液边界处的流体分子运动，从而获得流体分子的平动扩散特征时间τt和转动扩散时间τr，计算流体分子的纵向体弛豫t1b和横向体弛豫t2b；

5、s2：根据流体分子在固体表面吸附和解吸附过程，统计流体分子在固体表面的表面扩散时间τm和表面停留时间τs，从而计算流体分子的纵向表面弛豫t1s和横向表面弛豫t2s；

6、s3：根据公式(1)和(2)分别计算得到多孔介质固液边界处的等效纵向弛豫t1eff和等效横向弛豫t2eff，其中，公式(1)和公式(2)如下所示：

7、t1eff ＝ 1/(1/t1b+1/t1s)  (1)；

8、t2eff ＝ 1/(1/t2b+1/t2s)  (2)；

9、s4：将采用分子动力学模拟得到的等效纵向弛豫t1eff和等效横向弛豫t2eff作为小尺度边界处格子的弛豫特性，采用两层格子玻尔兹曼网格法模拟核磁共振弛豫特性，将获得的固液边界处的小尺度核磁共振弛豫特性传递到大尺度的空间中，从而得到固液边界处的大尺度核磁共振弛豫特性。

10、优选地，所述s4中，采用两层格子玻尔兹曼网格法模拟核磁共振弛豫特性的具体步骤如下：

11、s4-1：基于分子动力学模拟得到的等效纵向弛豫t1eff和等效横向弛豫t2eff，采用玻尔兹曼网格法模拟1000nm×1000nm×1000nm尺度的核磁共振弛豫特性；

12、s4-2：通过反演计算获得纳米尺度固液边界处的纵向驰豫分布和横向驰豫分布，分别取纵向驰豫分布和横向驰豫的最大峰值点作为纳米尺度固液边界处的等效纵向驰豫t1和等效横向驰豫t2；

13、s4-3：将1μm3作为一个单独的格子，将步骤s4-2获得的等效纵向驰豫t1和等效横向驰豫t2作为固液边界处格子的核磁共振弛豫特性，采用玻尔兹曼网格法模拟微米尺度的核磁共振弛豫特性；

14、s4-4：通过反演计算获得微米尺度的纵向驰豫分布t1′和横向驰豫分布t2′。

15、优选地，所述玻尔兹曼网格法为shan-chen lbm方法，使用的网格模型为d3q19网格模型。

16、优选地，采用所述玻尔兹曼网格法模拟核磁共振弛豫特性的具体方法如下：

17、a初始化所有格子的磁化矢量密度；

18、b按照公式(3)所示的lbm碰撞迁移公式计算平衡函数，所述公式(3)如下所示：

19、

20、其中，ξi是离散速度，i表示离散速度方向,x是函数f的位置坐标，t是当前时间步，fi(x,t)是流体分子在空间位置x沿着速度方向i的粒子密度分布函数，δt为格子时间；τvelocity是碰撞时间，fieq(x,t)是平衡分布函数；其中离散速度ξi遵循如下公式：

21、

22、c根据平衡分布函数计算碰撞迁移的磁化矢量密度，将每个格子内的磁化矢量密度乘以迁移几率进行该格子到相邻格子磁化矢量的迁移，然后与相邻格子内流体的磁化矢量密度进行加和，将加和的结果赋值给相邻格子；

23、d重新计算本次时间步长内所有格子的磁化矢量密度和；

24、e根据cpmg脉冲序列输出全部格子磁化矢量密度和的模作为回波信号；

25、f如果回波信号衰减至最大值的0.001倍，停止循环；

26、g对回波信号进行反演，从而得到整体的等效横向弛豫分布和等效纵向弛豫分布。

27、优选地，两层玻尔兹曼网格法模拟可以分别独立演化。

28、有益效果：本发明公开了一种用于提升分子动力学模拟核磁共振弛豫尺度的方法，具有如下优点：

29、(1)本发明采用双层玻尔兹曼(lbm)网格法，可以简便有效地将分子动力学(md)模拟结果升尺度到核磁共振物理实验可验证的尺度，为多孔介质的核磁共振弛豫模拟提供更加准确、便捷的数值实验方法。

30、(2)本发明通过不同尺度格子的独立运行，减少了大量的数据交换，有利于提高计算机并行计算的效率。

31、(3)本发明将分子动力学(md)模拟和核磁共振测量尺度相结合，相比于传统的核磁共振模拟，考虑了分子相互作用以及粒子碰撞，可以对多孔介质表面吸附、解析附直接进行响应，使得宏观核磁共振现象可以被微观模拟所解释。

技术特征：

1.一种用于提升分子动力学模拟核磁共振弛豫尺度的方法，其特征在于，具体步骤如下：

2.根据权利要求1所述的用于提升分子动力学模拟核磁共振弛豫尺度的方法，其特征在于，所述s4中，采用两层格子玻尔兹曼网格法模拟核磁共振弛豫特性的具体步骤如下：

3.根据权利要求1或2所述的用于提升分子动力学模拟核磁共振弛豫尺度的方法，其特征在于，所述玻尔兹曼网格法为shan-chen lbm方法，使用的网格模型为d3q19网格模型。

4.根据权利要求1所述的用于提升分子动力学模拟核磁共振弛豫尺度的方法，其特征在于，采用所述玻尔兹曼网格法模拟核磁共振弛豫特性的具体方法如下：

5.根据权利要求1所述的用于提升分子动力学模拟核磁共振弛豫尺度的方法，其特征在于，两层玻尔兹曼网格法模拟可以分别独立演化。

技术总结
本发明公开了一种用于提升分子动力学模拟核磁共振弛豫尺度的方法，具体步骤如下：S1：采用分子动力学方法模拟多孔介质固液边界处的流体分子运动，获取流体分子的纵向体弛豫T<subgt;1b</subgt;和横向体弛豫T<subgt;2b</subgt;；S2：获取流体分子的纵向表面弛豫T<subgt;1S</subgt;和横向表面弛豫T<subgt;2S</subgt;；S3：计算得到多孔介质固液边界处的等效纵向弛豫T<subgt;1eff</subgt;和等效横向弛豫T<subgt;2eff</subgt;；S4：采用两层格子玻尔兹曼网格法模拟核磁共振弛豫特性，将获得的固液边界处的小尺度核磁共振弛豫特性传递到大尺度的空间中，从而得到固液边界处的大尺度核磁共振弛豫特性。本发明解决了分子动力学模拟核磁共振弛豫结果在应用上的尺度匹配问题。

技术研发人员：梁灿,贾子健,李秀琪,周昕亮,顾安吉
受保护的技术使用者：常州工学院
技术研发日：
技术公布日：2024/1/12