连接时间周期和空间周期行波解的整体解及数值模拟方法

本发明涉及一种行波解的整体解及数值模拟方法，具体涉及一种连接时间周期和空间周期行波解的整体解及数值模拟方法。

背景技术：

1、在均匀介质中，y.fukao，y.morita and h.ninomiya找到了allen-cahn方程的一些完整解整个解趋向于两个行波解φ(x-ct-x1)和φ(-x-ct+x2)在x≈±∞，并最终收敛到1作为t→+∞。f.hamel得到了kpp方程的整个解，其特征在于两个行波解来自实轴的两侧，然后混合。x.chen and j.-s.guo通过研究两个行波解在x≈±∞相互移动然后在有限时间内湮灭的现象来构建整个解。h.matano构建了一种新型的整体溶液，趋向于t→-∞处的两个驼峰，但随着t的增加驼峰向原点移动，最终“碰撞”并形成一个单驼峰的最终形状的解。b.lou，j.suo and y.tan在狄利克雷边界条件下的半线上构造了一个新的全解，以fish-kpp方程，他们表明整个解是渐近平坦的，因为t→-∞但u(t，+∞)≡1。w.sheng and m.cao得到了连接两个不同行波解(t→-∞)和一个时周期解(t→+∞)的完整解。w.sheng andj.wang，构造了两种类型的整个解，其中一种类型的整个解表现为两个行波解，以不同的速度向同一方向移动，即当t增加时，较慢的波解会被追上并消失。而在空间周期介质中，w.liu and w.t.li证明了当t→-∞时，存在一个收敛于两个不同空间周期行波解的完整解。对于双稳态型方程，z.bu，z.wang and n.liu得到了连接不同行波解的三种完整解。

2、在扩散现象中，行波解对于描述这种现象和反应扩散方程的动力学是非常重要的，但要研究整个动力学，就需要研究一个通解，如，整个解，这是研究柯西问题动力学的关键点。实际上，行波解属于整个解。我们知道，有界解的ω-极限集是由整个解组成的。此外，它们的主要特征是同斜轨道或异斜轨道。许多学者研究了反应扩散方程的全解来描述扩散现象。

3、现有技术中对具有平流的fisher-kpp方程缺少更一般的完整解，未能完成反应扩散方程的动力学。

技术实现思路

1、本发明是为了解决上述问题而进行的，目的在于提供一种连接时间周期和空间周期行波解的整体解及数值模拟方法。

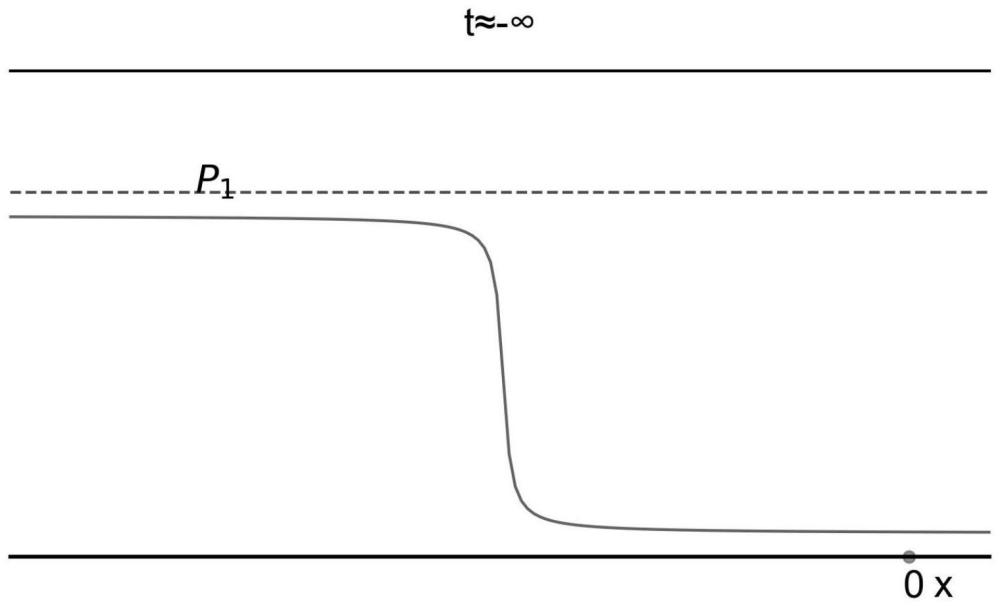
2、本发明提供了一种连接时间周期和空间周期行波解的整体解及数值模拟方法，具有这样的特征，通过python编写算法实现对时间周期行波解的整体解和空间周期行波解的整体解的数值模拟，包括：具有平流的fisher kpp方程ut＝uxx-βux+f(t，x，u)存在一个趋于ut的时间周期行波解的整体解ux+f1(t，u)(t→-∞)，随着t增加到+∞，收敛于空间周期行波解的整体解ut＝ux+f2(x，u)，通过python编写的数值模拟的具体算法为：set f1(t，u)＝u(1-u)，f2(x，u)＝u(1-0.5u)，且f(t，x，u)：＝(1-v(t))f1(t，u)+v(t)f2(x，u).。

3、在本发明提供的连接时间周期和空间周期行波解的整体解及数值模拟方法中，还可以具有这样的特征：其中，时间周期行波解的整体解小于空间周期行波解的整体解。

4、发明的作用与效果

5、根据本发明所涉及的连接时间周期和空间周期行波解的整体解及数值模拟方法，因为使用了一个依赖于空间和时间的渐近周期非线性项，得到了一个更一般的完整解。所以，本发明的连接时间周期和空间周期行波解的整体解及数值模拟方法为更一般的完整解，能完成反应扩散方程的动力学。

技术特征：

1.一种连接时间周期和空间周期行波解的整体解及数值模拟方法，其特征在于，通过python编写算法实现对时间周期行波解的整体解和空间周期行波解的整体解的数值模拟，包括：

2.根据权利要求1所述的连接时间周期和空间周期行波解的整体解及数值模拟方法，其特征在于：

技术总结
本发明提供了一种连接时间周期和空间周期行波解的整体解及数值模拟方法，通过python编写算法实现对时间周期行波解的整体解和空间周期行波解的整体解的数值模拟，包括：具有平流的Fisher KPP方程u<subgt;t</subgt;＝u<subgt;xx</subgt;‑βu<subgt;x</subgt;+f(t,x,u)存在一个趋于u<subgt;t</subgt;的时间周期行波解的整体解u<subgt;x</subgt;+f<subgt;1</subgt;(t,u)(t→‑∞)，随着t增加到+∞,收敛于空间周期行波解的整体解u<subgt;t</subgt;＝u<subgt;x</subgt;+f<subgt;2</subgt;(x,u)。总之，本方法为更一般的完整解，能完成反应扩散方程的动力学。

技术研发人员：袁效国,蔡静静
受保护的技术使用者：上海电力大学
技术研发日：
技术公布日：2024/9/5