一种基于Unity3D弹道导弹动力学三维仿真系统的制作方法

本发明涉及导弹动力学仿真，具体的，涉及一种基于unity3d弹道导弹动力学三维仿真系统。

背景技术：

1、弹道导弹动力学仿真技术是指通过计算机模拟弹道导弹的运动轨迹，以及在飞行过程中所受到的各种力和力矩，从而得到导弹的飞行状态和性能参数。在实际应用中，弹道导弹动力学仿真技术可以用于导弹的设计、试验、评估和改进等方面。

2、弹道导弹动力学包括弹道导弹轨道动力学和弹道导弹空气动力学。主要分为三个阶段：主动段，自由段和再入段；主动段由火箭发动机开始点火至将弹头提升至某一速度或高度后关闭发动机的过程；自由段即导弹飞出大气层，此阶段只受地球引力作用，对于无动力的弹道导弹来说其轨道类似于抛物线；再入段即导弹再入大气层，此阶段导弹利用自身的乘波体特性控制飞行，由于需要考虑导弹自身重力，导弹体所受地球大气的升力、阻力、侧滑力以及改变导弹姿态的扭矩，配合雷达、导弹制导和pid控制等，是弹道导弹面临困难最大的阶段。

3、弹道导弹动力学模型复杂，实验成本高。随着计算机技术的快速发展，采用软件仿真模拟弹道导弹动力学在一定程度上能够降低实验成本，通过三维可视化模型仿真，可以更加直观、形象地展现导弹的外形、飞行轨迹、速度、加速度、姿态等参数，让设计人员更好地了解和掌握导弹的设计特点和性能表现，从而进行有效的设计优化和改进。同时，弹道导弹的动力学三维仿真模型还能作用于数字化战场，便于指挥人员进行作战推演和战前预演。

4、但因其跨学科，研发成本高等特性。目前，弹道导弹动力学三维仿真的系统较少，将动力学模型与三维可视化模型结合的研究更少。且unity3d环境中rigid body的重力方向指向x-z平面，要实现三维环境下的地球引力作用还需重建引力模型。

技术实现思路

1、本发明的目的在于提供一种基于unity3d弹道导弹动力学三维仿真系统，用于解决当前弹道导弹动力学模型和三维可视化模型融合问题；同时提供一种解决在unity3d环境中rigid body无法模拟地球引力的问题；

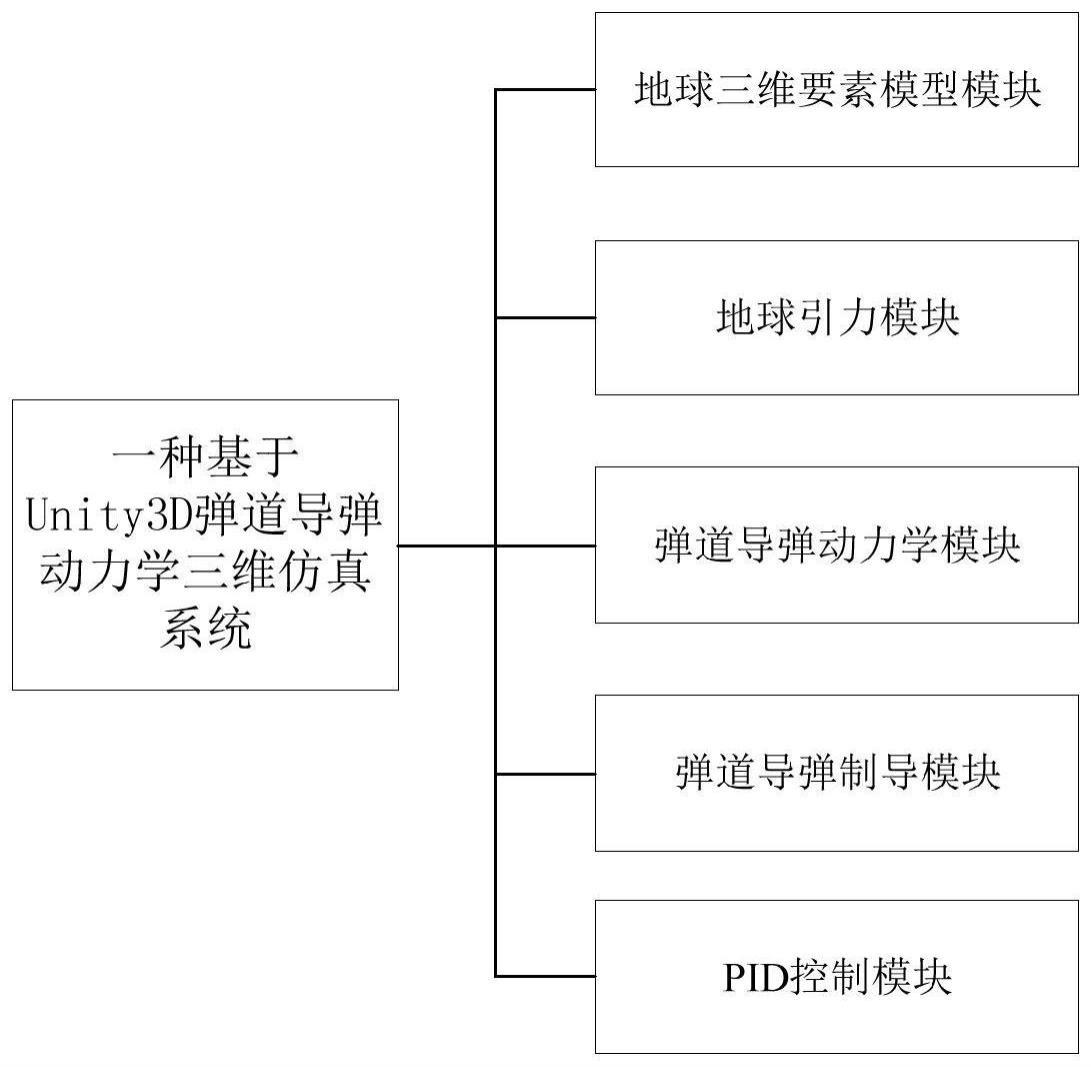
2、所述一种基于unity3d弹道导弹动力学三维仿真系统包括：地球三维要素模型模块，地球引力模块，弹道导弹动力学模块，弹道导弹制导模块，pid控制模块；

3、所述地球三维要素模型模块包括地球模型，地图模型，发射车模型，导弹模型，雷达模型，轨迹模型以及目标模型；

4、所述地球引力模块主要负责对地面物体，导弹飞行器的引力进行仿真模拟，由于unity3d的rigid body重力方向始终向下(垂直于x-z平面)，因此使用万有引力公式建立导弹的引力模型，其引力矢量f计算公式如下：

5、

6、其中g为引力常数，m为地球质量，m为导弹质量，r为地球半径，h为导弹的飞行高度，d表示引力的单位方向矢量，其计算公式如下：

7、

8、其中pm为导弹的三维坐标，pe为地球质心的三维坐标；

9、所述弹道导弹动力学模块主要包含轨道动力学和空气动力学，所述轨道动力学部分使用上述地球引力模块进行计算，主要对三维空间位置和速度进行建模，瞬时速度vt的计算公式如下：

10、

11、其中vt为导弹当前的瞬时速度矢量，vt-1为导弹的上一帧瞬时速度矢量，根据瞬时速度矢量和导弹的位置矢量可以计算出导弹的下一帧位置pt：

12、pt＝pt-1+vt×δt

13、所述空气动力学部分负责计算导弹在一定的攻角和侧滑角下所受到的升力大小fl，侧滑力大小fs和阻力大小fd，升力fl的计算公式如下：

14、

15、其中cl为导弹的升力系数，由导弹攻角，升降舵舵偏和当前速度确定，s为导弹最大横截面积，ρ为当前高度下的空气密度，侧滑力fs的计算公式如下：

16、

17、其中cs为导弹的侧滑力系数，由导弹侧滑角，方向舵舵偏和当前速度确定，阻力fd的计算公式如下：

18、

19、其中cd为导弹的阻力系数，由导弹合成攻角，舵偏和当前速度确定；

20、本发明为六自由度弹道动力学模型，能够实时仿真弹道导弹三个自由度的受力以及三个自由度的力矩；

21、在导弹的姿态控制上分别使用俯仰力矩mz，偏航力矩my和滚转力矩mx，其公式如下：

22、

23、式中，cz，cy，cx为无量纲的比例因子，分别为俯仰力矩因子、偏航力矩因子和滚转力矩因子；l为特征长度；

24、所述弹道导弹制导模块包含程序制导和终端制导；制导方式分别采用惯性制导和比例制导；所述惯性制导利用导弹内部的惯性传感器测量导弹的运动状态，然后通过数学模型计算导弹需要进行的调整，从而实现导弹的精确控制；惯性制导的指令公式如下：

25、δf＝kpp(t)+kvv(t)

26、其中，δf表示导弹需要进行的调整，kp和kv分别表示位置和速度的比例增益系数，p(t)表示t时刻的位置，v(t)表示t时刻的速度；

27、所述比例制导是在导弹飞行过程中，根据导弹与目标之间的相对位置和速度数据，计算出导弹需要调整的飞行方向和速度，实现精确打击的制导方式；其导引关系式为：

28、

29、其中q表示目标准线与基准线的夹角，σ表示导弹速度向量与基准线之间的夹角，k为比例系数；

30、所述pid控制模块通过对系统的反馈信号进行测量和分析，计算出误差值，并根据误差值调整控制输出，使系统能够快速、准确地达到期望值或稳定工作状态；其运算结果是由比例、积分和微分三个部分共同组成；其中，比例部分根据误差的大小进行调整，使系统快速响应；积分部分根据误差的持续时间进行调整，消除系统的静态误差；微分部分根据误差的变化率进行调整，减少系统的超调和震荡；

31、根据给定期望值r(t)与实际输出值y(t)构成控制偏差e(t),即e(t)＝r(t)-y(t)；对偏差e(t)进行比例、积分和微分运算,将三种运算的结果相加,得到pid控制器的控制输出u(t).在连续时间域中,pid控制器算法的表达式如下：

32、

33、式中，kp为比例系数，ti为积分时间常数，td为微分时间常数；

34、根据上述公式，可以计算出联合控制的制导指令，然后将制导指令输入到导弹的控制系统中，调整导弹的姿态和速度，使导弹能够准确地击中目标。

技术特征：

1.一种基于unity3d弹道导弹动力学三维仿真系统，其特征在于，包括地球三维要素模型模块，地球引力模块，弹道导弹动力学模块，弹道导弹制导模块，pid控制模块；

技术总结
本发明目的在于提供一种基于Unity3D弹道导弹动力学三维仿真系统，用于解决当前弹道导弹动力学模型和三维可视化模型融合问题；同时提供一种解决在Unity3D环境中Rigid Body无法模拟地球引力问题；所述一种基于Unity3D弹道导弹动力学三维仿真系统包括：地球三维要素模型模块，地球引力模块，弹道导弹动力学模块，弹道导弹制导模块，PID控制模块；所述地球三维要素模型模块包括地球模型，地图模型，发射车模型，导弹模型，雷达模型，轨迹模型以及目标模型；所述地球引力模块负责仿真模拟导弹引力；所述弹道导弹动力学模块包含轨道动力学和空气动力学；所述弹道导弹制导模块包含程序制导和终端制导；所述PID控制模块使系统时刻处于稳定工作状态。

技术研发人员：陈涛,匡敏驰,张晓涛,郭京京,任浩,曹向舒
受保护的技术使用者：北京誉飞科技发展有限公司
技术研发日：
技术公布日：2024/1/13