V型山谷地形中桩基的动力响应计算方法

本发明涉及抗震设计，更具体地涉及一种v型山谷地形中桩基的动力响应计算方法。

背景技术：

1、我国国土面积辽阔，但也是个多山国家，山地、丘陵、高原的面积占了国土面积的2/3以上。因此，使得我国很多地区都存在泥石流、滑坡等风险，尤其是在地震的作用下，会加大这类风险的发生几率，给路桥建设工程带来了很大的难度，影响了v型山谷桩基的稳定性。对此，正确分析地震作用下山区v型山谷桩基动力响应情况，有利于了解山区v型山谷桩基的实际情况，从而制定正确的施工计划，有利于提高桩基质量，保障人们的生命财产安全，实现其应有的效益。

2、相比于传统桩基的设计方法来说，山区v型山谷桩基承载设计要更为复杂，施工难度高。我国关于这方面的研究比较少。因此本文提出一种地震波作用下，v型山谷地形中桩基的位移计算方法，从而更加精准的计算出桩基的位移，防范工程事故的发生。现有技术对于v型山谷桩基础震动响应研究存在空白，目前国际上对v型山谷桩震动响应研究为通过极限法模拟震后v型山谷的残余变形，并将其转化为位移荷载计算v型山谷桩的静力受力与变形。这一方法存在着以下问题：

3、1.仅能模拟震后v型山谷残余位移对桩基础受力变形影响，而桩基础抗震安全性最低时往往处于地震过程而不是震后，这导致基于该方法的v型山谷桩基抗震设计理论无法计算v型山谷桩基抗震最不利情况。

4、2.v型山谷地形效应在地震过程中会显著增幅桩基础震动响应，而现有研究理论无法揭示这种增幅规律，基于现有理论进行v型山谷桩基础抗震设计会导致安全冗余度严重降低。

5、3.无法模拟地震过程中桩基础的震动规律，无法获得地震过程中桩基础的动力响应时程曲线。

技术实现思路

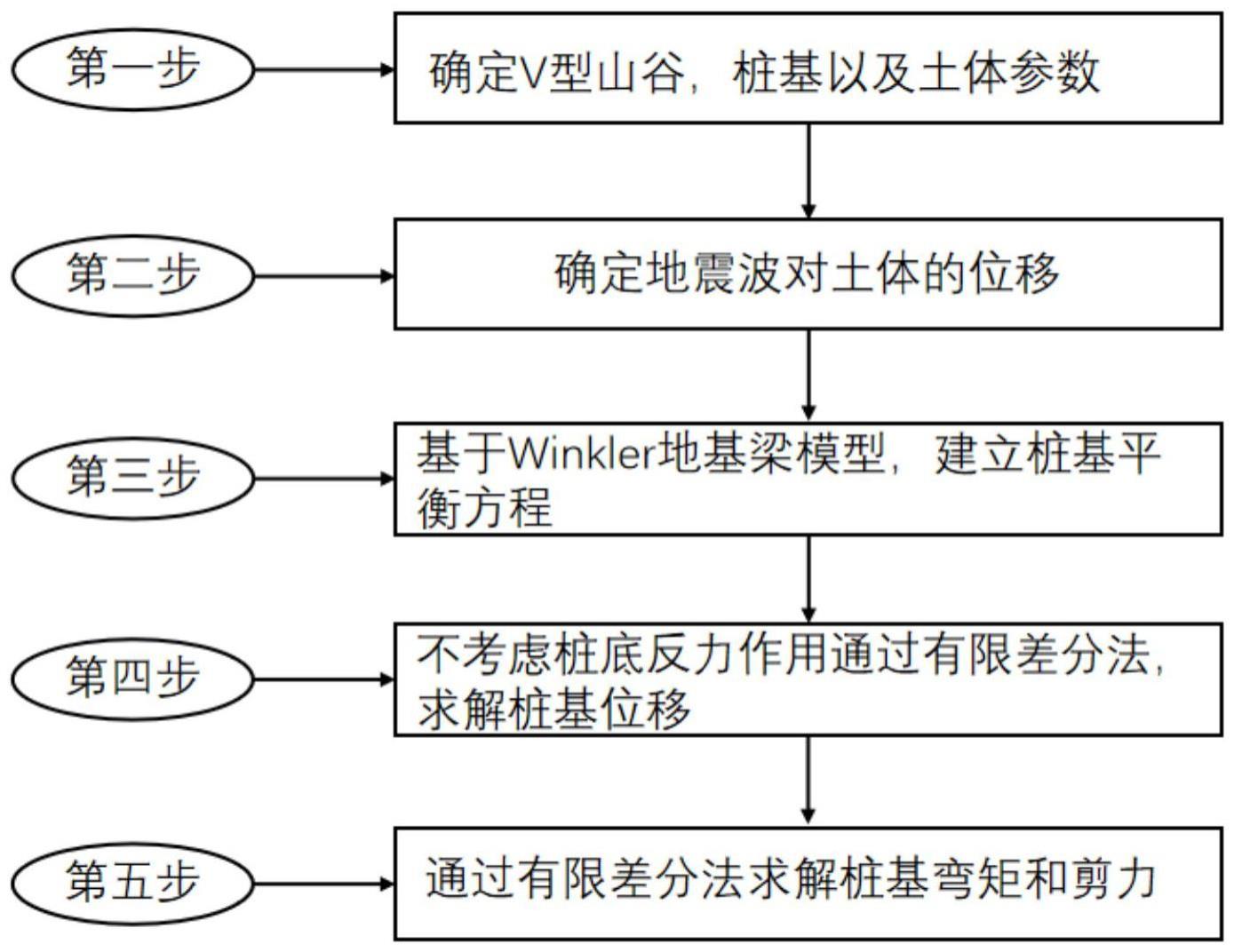
1、为了解决现有技术中v型山谷桩基础震动响应研究存在空白、极限法模拟震后v型山谷的残余变形存在的以上技术问题。本发明公开了一种v型山谷地形中桩基的动力响应计算方法，包含如下步骤：

2、(1)根据地勘资料获取v型山谷、桩基及土体的物理力学参数；

3、(2)基于graf加法定理计算得出由于地震波震动引起的土体位移场；

4、(3)基于动力winkler地基模型，将地震波引起的土体位移场转化为荷载，施加到桩基上，建立桩基的受力平衡方程；

5、(4)在桩顶、桩底均处于自由约束的情况下时，求解均布荷载引起的桩基位移及其所受的弯矩，剪力。

6、所述物理力学参数包括：

7、(1)山谷参数：山谷半径d，地震波无量纲频率为η，入射角角度α，峡谷的中心距离两边的距离b1，b2；

8、(2)桩基参数：等效直径d，入土深度l，桩基弹性模量ep，桩惯性矩ip；

9、(3)土体参数：弹性模量es，土体泊松比μs。

10、所述土体外域位移场uouter(r,θ)计算方法为：

11、uouter(r，θ)＝uf(r，θ)+us1(r，θ)+us2(r，θ)；  (1)

12、其中，外域自由场uf(r，θ)，外域散射场1us1(r，θ)，外域散射场2us2(r，θ)的计算方法分别为：

13、

14、

15、

16、内域散射场uinner1(r，θ)与内域散射场uinner2(r，θ)的计算公式分别为：

17、

18、

19、

20、

21、

22、

23、其中，α为地震波入射角度；r是以o点为圆心的极半径，θ为极角；k为入射波波数，其中η为入射波无量纲频率；εn为纽曼系数(ε0＝1，n＝0；εn＝2，n>0)；h(1)(·)是n阶第三类贝塞尔函数，jn(·)是n阶第一类贝塞尔函数；an，bn，cn，dn是要确定的系数，m和n代表级数，v代表v型山谷参数。

24、所述桩基的受力平衡方程如下：

25、

26、其中，w(y)为桩基的位移函数；ep为桩基弹性模量；ip为桩基横截面惯性矩；d为等效宽度；k1为桩侧土的弹簧刚度；es为土体弹性模量；μs为土体泊松比；p(y)为桩基受到的竖向外荷载。

27、

28、p(y)＝k1×wf(y)；  (13)

29、

30、式中，wf(y)为土体自由场位移；x为桩基放置的位置。

31、求解集中荷载引起的桩基剪力q和弯矩m如下：

32、可将上述方程写成有限差分的形式：

33、αwi-2+βwi-1+γwi+βwi+1+αwi+2＝pi；  (15)

34、式中，

35、结合边界条件可推导出单桩位移的方程：

36、

37、此处的k可以看做一个从n+1*n+1的矩阵；

38、而刚度矩阵如下：

39、

40、采用有限差分法求解上式。将桩基划分为n段，每段的高度为h＝l/n，l为桩长。桩基节点编号从桩顶至桩端依次为0，1，…，n-1，n。计算时分别在桩顶和桩端处增加两个虚拟节点-2，-1，n+1，n+2。

41、桩身弯矩如下：

42、

43、桩身剪力如下：

44、

45、本发明的技术方案有益效果在于：首次采用动力winkler地基模型结合波函数求解了v型山谷桩基础震动响应，获得了v型山谷桩基地震过程中得动力时程曲线，并能揭示v型山谷地形效应对桩震动响应的增幅规律。

技术特征：

1.一种v型山谷地形中桩基的动力响应计算方法，其特征在于，包括如下步骤：

2.如权利要求1所述的v型山谷地形中桩基的动力响应计算方法，其特征在于，在步骤(2)中，所述由于地震波震动引起的土体位移场包括地震波入射形成的外域位移场，地震波入射形成的外域位移场的计算方法为：

3.如权利要求2所述的v型山谷地形中桩基的动力计算方法，其特征在于，在步骤(2)中，所述土体位移场包括内域位移场uinner1(r,θ)和内域位移场uinner2(r,θ)，内域位移场uinner1(r,θ)和内域位移场uinner2(r,θ)的计算方法分别为：

4.如权利要求3所述的v型山谷地形中桩基的动力响应计算方法，其特征在于，在步骤(3)中，所述桩基的受力平衡方程为：

5.如权利要求4所述的v型山谷地形中桩基的动力响应计算方法，其特征在于，在步骤(4)，所述在桩顶、桩底均处于自由约束的情况下时，求解均布荷载引起的桩基位移w的计算公式为：

6.如权利要求5所述的v型山谷地形中桩基的动力响应计算方法，其特征在于，在步骤(4)，所述在桩顶、桩底均处于自由约束的情况下时，求解均布荷载引起的弯矩m和桩基剪力q的计算公式分别为：

技术总结
本发明涉及一种V型山谷地形中桩基的动力响应计算方法，包括如下步骤：(1)获取山谷、桩基及土体的物理力学参数；(2)基于Graf加法定理计算得出由于地震波震动引起的土体位移场；(3)基于动力Winkler地基模型，将地震波震动引起的土体位移场转化为荷载施加到桩基上，建立桩基的受力平衡方程；(4)在桩顶、桩底均处于自由约束的情况下时，求解均布荷载引起的桩基位移及其所受的弯矩，剪力。上述方法通过结合Graf加法定理与Winkler地基梁模型，首次提出了V型山谷上桩基础震动响应闭合解，并准确揭示V型山谷地震放大效应对桩基础震动响应的影响。

技术研发人员：可文海,李源,管凌霄,吴磊,杨文海,丁海滨,岳成
受保护的技术使用者：华东交通大学
技术研发日：
技术公布日：2024/1/13