一种用于随机振动的可靠度计算方法及系统与流程

本发明涉及机械结构可靠性设计，特别是涉及一种用于随机振动的可靠度计算方法及系统。

背景技术：

1、可靠性设计是结构安全设计理念的重大发展，从结构的静强度分析到疲劳强度分析再到结构的可靠度计算，反映了结构强度计算上的两次重要变革。经过早年长时间的研究积累，静强度可靠性设计体系发展已比较成熟，但是仍然会有大量的机械产品面临疲劳失效问题，据统计，机械结构的失效问题有50％～90％由疲劳载荷引起。而现今，随着机械结构大型化、复杂化及多元化的发展趋势，失效过程中的随机因素更是层出不穷，疲劳寿命的不确定性问题也愈发凸显。为提高产品设计水平与质量，对其中关键构件进行可靠性设计已势在必行。由于工程构件多是因承受随机载荷作用而失效，因此寻求随机加载情况下适用的构件随机疲劳可靠性设计方法是极为重要的。

2、围绕机械结构疲劳寿命的概率分析，传统上多基于应力–强度干涉模型描述载荷不确定性对构件疲劳可靠度的影响。应力-强度干涉模型是零部件可靠性设计的基本模型。在可靠性计算中，进行随机变量“干涉分析”的基本思想是，在同一坐标系中画出的应力和强度这两个随机变量的概率密度函数曲线一般都会相交，即存在“干涉”，也就意味着可能有应力大于强度的可能性。

3、不同于疲劳问题中常见的恒幅载荷或变幅载荷，随机振动是一种具有明显随机性的振动载荷，无法用具体的时域历程来描述，一般使用功率谱密度函数来表达。由于传统疲劳计算需要基于每次载荷循环来计算结构疲劳损伤，面对没有明确历程的随机振动则难以直接求解，一般使用频域方法进行概率计算，通常以期望疲劳寿命的形式给出结果。而相比较之下结构在随机载荷作用下的可靠度计算则更有参考价值。传统中对于随机振动下结构的强度计算仅仅给出一个疲劳寿命的期望值，而由于随机振动的载荷随机性，导致结构的实际寿命可能存在较明显的分散性，因此计算出的寿命期望值很难对结构的设计与强度校核提供直接参考。

技术实现思路

1、本发明的目的是提供一种用于随机振动的可靠度计算方法及系统，使用频域方法得到结构受到的随机载荷分布，并使用应力-强度干涉模型求解可靠度，对结构的设计与强度校核提供更有价值的参考信息，具备更广泛的适用性。

2、为实现上述目的，本发明提供了如下方案：

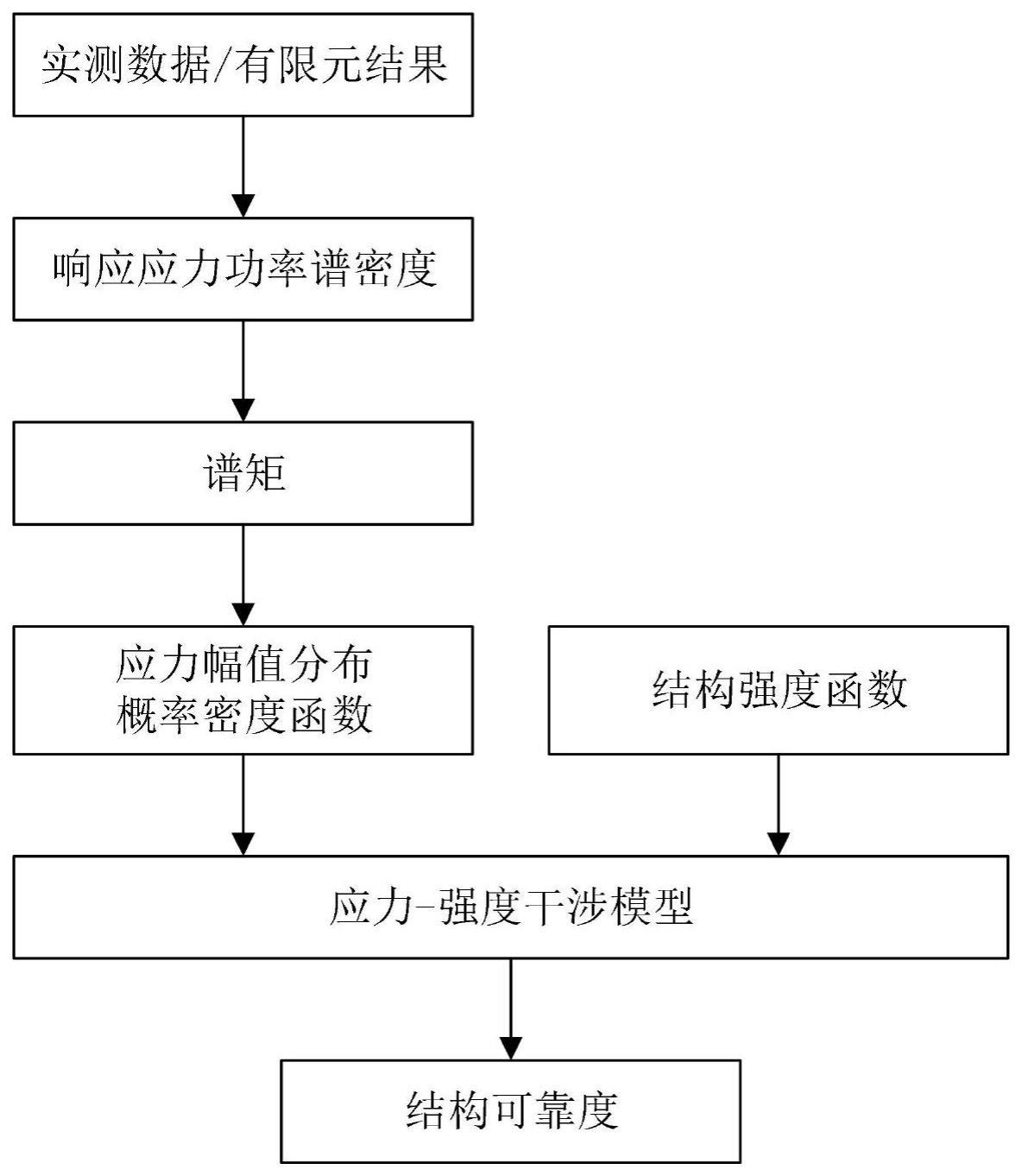
3、一种用于随机振动的可靠度计算方法，该方法包括以下步骤：

4、1)，通过有限元模型或实测得到结构危险点的随机响应应力的功率谱密度函数g(f)，其中f为频率；

5、2)，基于功率谱密度函数g(f)，计算随机响应应力的功率谱密度函数的谱矩参数mi，其中，i代表谱矩的阶数，i＝0,1,2,...；

6、3)，根据谱矩参数mi计算随机响应应力的不规则因子γ；

7、4)，基于步骤1)-步骤3)得到功率谱密度函数g(f)、谱矩参数mi、不规则因子γ，计算随机响应应力的幅值概率密度函数p(s)；

8、5)，假设结构所用材料的强度s服从正态分布，且其均值与标准差均与时间t相关，确定材料强度s的概率密度函数f(s)；

9、6)，将步骤4)中的幅值概率密度函数p(s)与步骤5)中的材料强度的概率密度函数f(s)代入应力-强度干涉模型，得到在t时刻结构的可靠度r(t)：

10、

11、进一步地，所述步骤2)中，谱矩参数mi的表达式如下：

12、

13、进一步地，所述步骤3)中，不规则因子γ的表达式如下：

14、

15、进一步地，所述步骤4)中，幅值概率密度函数p(s)：

16、

17、其中，s代表应力幅值，单位为mpa；其余字母的表达式分别为：

18、

19、

20、

21、进一步地，所述步骤5)中，材料强度s的概率密度函数表达式为：

22、

23、其中，μ(t)为在t时刻结构的强度均值，单位为mpa；σ(t)为t时刻结构的强度标准差；μ(t)与σ(t)基于强度退化模型得到。

24、进一步地，所述步骤1)中，通过有限元模型或实测得到结构危险点的随机响应应力的功率谱密度函数g(f)，具体包括：

25、基于有限元模型，得到结构在设计随机激励下的有限元模拟结果，确定结构危险点的随机响应应力的功率谱密度函数g(f)；

26、或者，基于结构服役状态的实测信号值，得到结构危险点的随机响应应力的功率谱密度函数g(f)。

27、本发明还提供一种用于随机振动的可靠度计算系统，包括：

28、功率谱密度函数确定模块，用于通过有限元模型或实测得到结构危险点的随机响应应力的功率谱密度函数g(f)，其中f为频率；

29、谱矩参数计算模块，用于基于功率谱密度函数g(f)，计算随机响应应力的功率谱密度函数的谱矩参数mi，其中，i代表谱矩的阶数，i＝0,1,2,...；

30、不规则因子计算模块，用于根据谱矩参数mi计算随机响应应力的不规则因子γ；

31、幅值概率密度函数计算模块，用于基于功率谱密度函数g(f)、谱矩参数mi、不规则因子γ，计算随机响应应力的幅值概率密度函数p(s)；

32、概率密度函数确定模块，用于假设结构所用材料的强度s服从正态分布，且其均值与标准差均与时间t相关，确定材料强度s的概率密度函数f(s)；

33、可靠度计算模块，用于将幅值概率密度函数p(s)与材料强度的概率密度函数f(s)代入应力-强度干涉模型，得到在t时刻结构的可靠度r(t)：

34、

35、本发明还提供一种电子装置，包括一个或多个处理器；存储器；一个或多个应用程序，其中所述一个或多个应用程序被存储在所述存储器中并被配置为由所述一个或多个处理器执行，所述一个或多个程序配置用于执行如上述的用于随机振动的可靠度计算方法。

36、本发明还提供一种非暂态计算机可读存储介质，其上存储有计算机程序，所述计算机程序被处理器执行时实现如上述的用于随机振动的可靠度计算方法。

37、根据本发明提供的具体实施例，本发明公开了以下技术效果：本发明提供的用于随机振动的可靠度计算方法及系统，以结构危险点的响应应力功率谱密度出发，结合随机应力幅值分布模型与应力-强度干涉模型，求出结构在某一时刻的可靠度，并能够直接得到结构在随机载荷下的可靠度。相比于传统的随机振动疲劳强度校核方法，本发明对结构设计与优化提供更有价值的参考信息，具备更广泛的适用性。

技术特征：

1.一种用于随机振动的可靠度计算方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的用于随机振动的可靠度计算方法，其特征在于，所述步骤2)中，谱矩参数mi的表达式如下：

3.根据权利要求2所述的用于随机振动的可靠度计算方法，其特征在于，所述步骤3)中，不规则因子γ的表达式如下：

4.根据权利要求3所述的用于随机振动的可靠度计算方法，其特征在于，所述步骤4)中，幅值概率密度函数p(s)：

5.根据权利要求4所述的用于随机振动的可靠度计算方法，其特征在于，所述步骤5)中，材料强度s的概率密度函数表达式为：

6.根据权利要求4所述的用于随机振动的可靠度计算方法，其特征在于，所述步骤1)中，通过有限元模型或实测得到结构危险点的随机响应应力的功率谱密度函数g(f)，具体包括：

7.一种用于随机振动的可靠度计算系统，其特征在于，包括：

8.一种电子装置，其特征在于：

9.一种非暂态计算机可读存储介质，其上存储有计算机程序，其特征在于，所述计算机程序被处理器执行时实现如权利要求1至6任一项所述的用于随机振动的可靠度计算方法。

技术总结
本发明属于机械结构可靠性设计技术领域，公开了一种用于随机振动的可靠度计算方法及系统，所述方法基于结构服役状态的实测信号值或基于结构在一定设计随机激励下的有限元模拟结果得到结构危险点的响应应力功率谱密度，结合随机应力幅值分布模型与应力‑强度干涉模型，求解得到结构在某一时刻的可靠度。相比于传统的随机振动疲劳强度校核方法，本发明无需进行频域到时域的转换，能够基于应力‑强度干涉模型来分析结构的服役状态，进而实现可靠性分析。该发明为结构设计与优化提供更有价值的参考信息，具备更广泛的适用性。

技术研发人员：赵松涛,赵丙峰,张晓旭,韩莹莹,穆童,高长伟,孙侨,赵明达,韦军伟,王天昊
受保护的技术使用者：中国船舶重工集团公司第七0三研究所
技术研发日：
技术公布日：2024/1/15