适用于电路仿真软件的稀疏矩阵迭代法预处理构造方法

本发明涉及电路仿真软件领域，特别是涉及一种适用于最小广义残量迭代法的预处理技术。

背景技术：

1、求解大型线性方程组时，可以使用迭代法进行求解。现有的电路仿真软件如hspice使用的求解器中包括有使用最小广义残量法的选项。

2、广义最小残量法(generalized minimal residual，gmres)是在共扼残量法的基础上发展起来的，是一种求解线性方程组时采用最优迭代次序保证残向量最小的算法，是公认地求解大型非对称线性方程组的有效方法之一。

3、实际应用中的大规模稀疏矩阵方程组通常具有特定的稀疏结构和元素量阶分布，其系数矩阵通常有很强的整体病态性，导致收敛速度很慢甚至无法收敛。只有结合系数矩阵的系数结构和特性，设计特定的预处理，最小广义残量法才能有效使用。

4、最小广义残量法的预处理是指对性方程组进行适当的变换，改善矩阵的谱性质加快收敛速度。有效的预处理能够减少最小广义残量法方法收敛所需要的次数，对提高求解效率具有重大意义。

5、lu分解法是将非奇异矩阵a拆成上三角矩阵u和下三角矩阵l相乘的形式(即a＝lu)，lu分解在直接法和迭代法中都有应用。

6、ilu分解方法与lu分解类似，但是lu分解中a＝lu，ilu中a≈lu，且l、u和a具有相同的稀疏性。ilu(ε)分解中可以选择不同的非零元填充级别或者填充方式，根据需要，在部分位置填充(或不填充)非零元。分解时根据ε的尺寸产生相应的一些填充量，其预处理效果优于ilu(0)，但增加了计算量、难以保证l和u的稀疏性。因此，ilu(ε)的关键就是寻找一种平衡——不能产生太多的填充量，又要达到预期的预处理效果，即ε的选取。

技术实现思路

1、技术问题：本发明的目的是提供一种适用于电路仿真软件的稀疏矩阵迭代法预处理构造方法，适用于电路仿真软件中稀疏矩阵的分布特点，能够更好地改善矩阵的谱性质，加快迭代方法的收敛速度。

2、技术方案：本发明的一种适用于电路仿真软件的稀疏矩阵迭代法的预处理子构造方法，根据电路仿真软件中的稀疏矩阵的元素分布特点提出了不同的不完全lu分解方法，在对位置在(i，j)的元素进行分解时，进行如下步骤：

3、步骤1，筛选元素：

4、|aij|*|aji|<ω2ajjaii (1)

5、判定是否保留当前分解的元素，其中aij，aji表示矩阵中的一对对称元素，ω∈[0，1]，是一个经验数值；

6、步骤2，调整对角线元素：假如这对元素未通过筛选被剔除，则按照以下公式对对角线上的元素做出调整，

7、aii＝aii+x*y (2)

8、ajj＝ajj+x/y (3)

9、其中x＝(|aij|*|aji|)1/2，y＝(|aii|*|ajj|)1/2

10、该方法基于lu分解法，lu分解法是将非奇异矩阵a拆分成上三角矩阵u和下三角矩阵l相乘的形式，下三角矩阵l和上三角矩阵u的乘积等于原始非奇异矩阵a，即a＝lu；

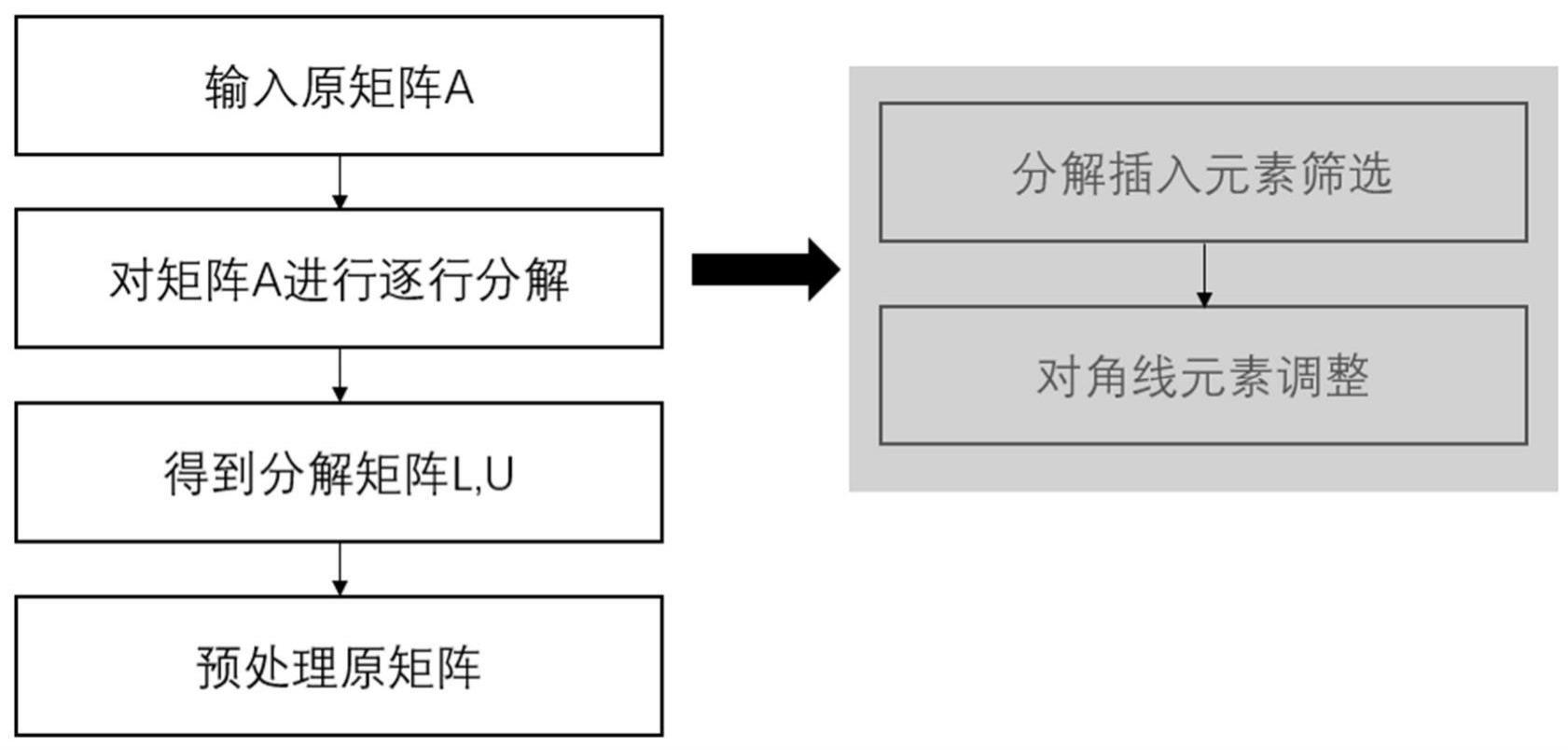
11、为保留原矩阵的稀疏性，在lu分解的过程中需要控制插入元素的数量，具体分为两个步骤：矩阵对角线调整和分解插入元素筛选；

12、对于一个稀疏矩阵进行预处理时，使用不带填充元素的不完全lu分解法即ilu(0)分解，ilu(0)分解方法与lu分解类似；lu分解中a＝lu，ilu中a≈lu，且l、u和a具有相同的稀疏性，即分解后的l，u矩阵中的元素只能在原矩阵中有元素的位置插入分解元素；所述预处理通过矩阵分解插入元素筛选、对角线元素调整两个步骤进行预处理子构造。

13、其中，

14、所述矩阵对角线调整具体为：

15、电路仿真中出现的待求解矩阵通常主对角线总是有分布元素的，矩阵中的非零元素反映的是电路中各器件互相之间的电气性质影响，对角线上的元素代表的含义是器件自身的电气性质；

16、利用该矩阵结构，使用对角线上的元素值作为筛选分解插入元素的参照值，为了保证稳定性，首先将对角线上的元素做一些调整；

17、按照式(2)和式(3)更改对角线上的元素：

18、aii＝aii+x*y (2)

19、ajj＝ajj+x/y (3)

20、其中，x＝(|aij|*|aji|)1/2，y＝(|aii|*|ajj|)1/2；当a对称且正定时，修改后的矩阵的特征值不会小于原始矩阵a的相应特征值，因为修改矩阵r是正半定的；因此，对角线修正保留了修改后矩阵的正定性质；当a是非对称且正实数即a的对称部分是正定的时，证明对角线修正将保持修改后矩阵的正实数性质，这个不完全因式分解不会对条件产生不利影响。

21、所述分解插入元素筛选为：

22、根据电路仿真软件中出现的稀疏矩阵分布特点，预处理子构造方法不要求l、u和a具有相同的稀疏性，非零元素的取舍是根据a中相应位置上的元素与其相关联的对角元素的相对关系确定的。

23、所述的预处理子构造是使用不完整的上三角矩阵u、下三角矩阵l分解，即l*u*分解，l*u*＝a-r≈a；l，u矩阵都会插入一些分解得到的元素，r是剩余矩阵，含有所有被剔除元素的矩阵，不强制保证原矩阵a的稀疏性；在每一次分解消元的过程中，都对将要分解的元素aij和aji进行取舍，符合式(1)的aij和aji被拒绝加入，

24、|aij|*|aji|<ω2ajjaii (1)

25、其中，ω∈[0，1]；由于电路仿真中稀疏矩阵的结构对称性高，分解后的l，u矩阵也是高度结构对称的，即预处理法决定是否插入分解得来的元素时，插入的分解元素会得到筛选机会，并通过设置的阈值进行挑选；

26、经过矩阵对角线调整和分解插入元素筛选后得到的l和u因子矩阵用于预处理矩阵a，得到式(4)

27、l*-1au*-1u*x＝l*-1b (4)

28、当l*-1au*-1接近于一个单位矩阵时，它的谱半径会比原矩阵a小，并因此更快地收敛，用于加速最小广义残量法的收敛。

29、有益效果：本发明适用于电路仿真软件的稀疏矩阵迭代法预处理构造方法的技术方案带来的优点为：

30、使用本方法构造的预处理子l，u对比其他方法，更加适合电路仿真软件中稀疏矩阵的分布特点，保留了原矩阵中相对较大的元素值，有效抑制了剩余矩阵的模的增大。经过这个预处理子处理的矩阵具有更小的条件数,更好的特征值分布,即矩阵的谱性质得到了更好的改善，可以加快迭代方法的收敛速度。适用于电路仿真软件中稀疏矩阵的分布特点，能够更好地改善矩阵的谱性质，加快迭代方法的收敛速度。

技术特征：

1.一种适用于电路仿真软件的稀疏矩阵迭代法的预处理子构造方法，其特征在于，

2.根据权利要求1所述的适用于电路仿真软件的稀疏矩阵迭代法预处理构造方法，其特征在于，所述矩阵对角线调整具体为：

3.根据权利要求1所述的适用于电路仿真软件的稀疏矩阵迭代法预处理子构造方法，其特征在于，所述分解插入元素筛选为：

4.根据权利要求1所述的适用于电路仿真软件的稀疏矩阵迭代法预处理子构造方法，其特征在于，所述的预处理子构造是使用不完整的上三角矩阵u、下三角矩阵l分解，即l*u*分解，l*u*＝a-r≈a；l，u矩阵都会插入一些分解得到的元素，r是剩余矩阵，含有所有被剔除元素的矩阵，不强制保证原矩阵a的稀疏性；在每一次分解消元的过程中，都对将要分解的元素aij和aji进行取舍，符合式(1)的aij和aji被拒绝加入，

技术总结
本发明涉及到集成电路版图设计领域，尤其是涉及一种适用于电路仿真软件的预处理构造框架，该方法包括：对输入矩阵进行LU分解处理，结合对角线元素调整和分解插入元素筛选对分解矩阵进行调整，使用求得的分解矩阵L，U矩阵对原矩阵进行预处理，从而实现改善矩阵的谱性质，从而加速最小广义残量法的收敛。使用本方法构造的预处理子L，U对比其他方法，更加适合电路仿真软件中稀疏矩阵的分布特点，保留了原矩阵中相对较大的元素值，有效抑制了剩余矩阵的模的增大。经过这个预处理子处理的矩阵具有更小的条件数,更好的特征值分布,即矩阵的谱性质得到了更好的改善，可以加快迭代方法的收敛速度。

技术研发人员：王学香,冯文龙,刘昊,曹鹏,杨军
受保护的技术使用者：东南大学苏州研究院
技术研发日：
技术公布日：2024/1/16