用于提高工业仿真软件线弹性求解精度的数值方法与流程

本发明属于工业仿真软件改进，尤其涉及一种用于提高工业仿真软件线弹性求解精度的数值方法。

背景技术：

1、有限元q1线性弹性数值求解是一种常见的数值计算方法，用于近似求解线性弹性力学问题。其中，有限元方法(finite element method，简称fem)是一种数值逼近技术，将连续的物理问题离散化为有限数量的子区域(单元)，并在每个单元上建立逼近函数，通过组装这些单元，形成整个离散化域，并通过数值计算求解近似解。q1元素是一种常用的有限元单元，它采用一阶多项式(线性函数)来逼近解的形状。对于二维问题，q1元素通常是四边形或三角形，对于三维问题，q1元素通常是六面体或四面体。q1元素的形状函数在每个单元内部是线性的。线性弹性力学是一种用于描述物体在受力作用下的弹性变形行为的力学理论。线性弹性力学假设材料的应力与应变之间存在线性关系，并满足胡克定律，基于线性弹性力学理论，可以建立弹性力学问题的数学模型。

2、有限元q1线性弹性数值求解将线性弹性力学问题转化为一个变分问题，通过将问题的弱形式离散化，并利用有限元q1元素来逼近未知解。通过建立刚度矩阵和载荷向量，使用数值算法(如线性求解器)来解决离散化问题，从而获得近似的弹性应变和位移场。求解过程的数值实现可以采用速度形式(velocity formulation)和速度-压力形式(velocity-pressure formulation)两种形式。现存的大多数速度求解的方式中存在着压力不精确等问题，因为速度形式不直接求解压力场，因此对于需要准确压力信息的问题，速度形式可能无法提供精确解。另外还存在压力梯度缺失的问题，由于速度形式无法直接计算压力梯度，这对于某些问题(如涡量计算)可能产生限制。

3、在具体的数值求解过程中，还需要考虑边界条件的处理、网格划分和生成、求解器的选择和收敛性分析等方面。这些基本概念提供了有限元q1线性弹性数值求解的框架和理论基础，以便进行弹性力学问题的数值求解和工程应用。

4、有限元q1线性弹性数值求解方法在工业仿真cae软件中有广泛的应用。工业仿真软件使用有限元方法来模拟和分析各种工程问题，如结构力学、热传导、流体力学等。有限元q1线性弹性数值求解方法的主要优势之一是其适用于各种复杂几何形状和材料性质的问题。它可以用于处理不同类型的结构，包括固体、液体和气体。该方法对于工程问题的建模和分析提供了灵活性和精确性，其通常在工业仿真软件中执行以下任务：

5、1、结构分析：对于机械部件、零件或装配体的应力、应变、变形等进行分析，以评估其性能和安全性。

6、2、热分析：用于模拟热传导和热扩散问题，例如温度分布、热应力和热变形分析。

7、3、动力学分析：用于模拟结构的振动、冲击和动态响应，以评估其在动态载荷下的行为。

8、通过在工业仿真cae软件中实现有限元q1线性弹性数值求解方法，工程师和设计师能够进行更准确和可靠的工程分析，并对设计和材料选择做出更明智的决策。这种方法已经成为工程实践中不可或缺的工具之一，广泛应用于航空航天、汽车、能源、建筑等行业。

技术实现思路

1、为了进一步提高工业仿真软件线性弹性求解精度，使其更好地模拟和分析各种工程问题，在工业仿真软件中更好地实现结构分析、热分析、动力学分析的功能，本发明提出了一种用于提高工业仿真软件线弹性求解精度的数值方法。

2、本发明提供了一种在工业仿真软件中使用有限元法来近似求解椭圆型和/或抛物型偏微分方程(pdes)的计算方法。有限元法基于对这些方程的变分形式进行离散化处理的原理。离散化处理实际上是对这些pdes进行变分重述，其中使用具有有限维近似空间的变分空间来计算近似解。为了定义这个空间，需要对研究几何域ω进行空间离散化，从而确定一个相似或近似的几何域ωh。该几何域由不相交的基本几何实体(例如三角形、四边形、四面体等)组成，这些实体具有直线或曲线形状。因此，该近似空间中的每个函数在每个几何实体中的限制对应一个多项式函数。多项式的性质和次数取决于它所定义的几何实体。本发明提出了一种涉及热力学力学演化问题的椭圆型和抛物型pdes的数值解法，其中包括热弹性粘塑平衡问题和热扩散问题。

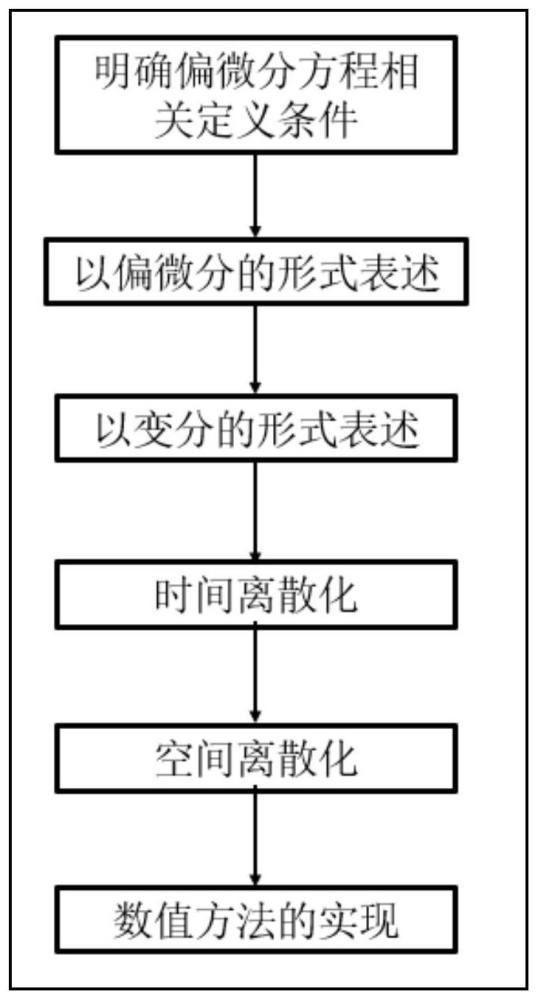
3、具体地，本发明提供了一种用于提高工业仿真软件线弹性求解精度的数值方法，本方法包括：

4、s1.明确偏微分方程相关定义条件；

5、s2.以偏微分的形式表述；

6、s3.以变分的形式表述；

7、s4.时间离散化；

8、s5.空间离散化；

9、s6.数值方法的实现。

10、进一步地，本发明用于提高工业仿真软件线弹性求解精度的数值方法步骤s1中所述明确偏微分方程相关定义条件，包括：

11、明确求解的pdes类型、边界条件、几何域以及相关参数；

12、对于热机械演化问题，在三维欧几里德向量空间e以及与之相关联的仿射空间e中，假设存在一个直角坐标系(o,e0,e1,e2)，其满足以下条件：

13、包含一个具有足够规则边界的几何构型ω，设其为各向同性固体材料，以及笛卡尔坐标系(x0,x1,x2)每个点x∈ω，其中x＝xiei；

14、对于热力学问题的边界条件，有三种ω构型，其中三个表面和称为dirichlet边界，其值不为零；

15、对于热问题的边界条件，划分其中分别代表dirichlet边界、neumann边界和robin边界的表面；

16、分别定义在三个neumann边界表面和上的三个标量表面力场和

17、三个标量位移场和分别定义在三个dirichlet边界表面和上；

18、在域ω内定义的体积力场f。

19、进一步地，本发明用于提高工业仿真软件线弹性求解精度的数值方法步骤s2中所述以偏微分的形式表述，包括：

20、在小扰动假设下，将热弹性粘塑性平衡问题记为(p)，根据假设热力耦合较弱，忽略热方程中的热力耦合项，熵和比热取决于温度，此时，从(p)中提取的热问题(pt)和力学问题(pm)分别表示为以下形式的偏微分方程：

21、

22、

23、其中：

24、

25、

26、

27、

28、t、cp和s分别表示温度场、质量热场和熵场；

29、q、k和q分别表示热通量向量、热导率和体积热功率；

30、

31、表示几何变换的行列式；

32、表示二阶恒等张量；

33、u表示位移场；

34、td和qn分别表示在和上施加的温度和热通量；

35、t∞、h、σ和ε分别表示环境温度、对流系数、玻尔兹曼常数和热发射率；

36、分别表示速度场、应变率张量和其偏差分量；

37、和分别表示弹性变形速率张量和粘塑性变形速率张量；

38、表示柯西应力张量；

39、和分别指定σ的偏转分量和压力场；

40、表示nc个内部的运动硬化变量；

41、和分别表示nc个运动硬化变量和运动硬化张量；分别表示von mises等效应力、累积塑性应变速率和随着ε变量增加的各向同性硬化函数；

42、μ(t)＞0和x(t)＞0分别表示剪切模量和压缩模量；

43、kvp(t)＞0和m(t)＞0分别表示粘塑性稠度和灵敏度；

44、

45、和分别表示在和的dirichlet边界上施加的速度；

46、和分别表示在和的neumann边界上施加的表面力。

47、进一步地，本发明用于提高工业仿真软件线弹性求解精度的数值方法步骤s3中所述以变分的形式表述，包括：

48、将pdes问题转化为一个等效的变分问题；

49、在变分形式下，热问题(pt)的公式如下：

50、

51、并且，

52、力学问题(pm)采用两种形式的表述：速度形式和速度-压力形式

53、速度形式的表述如下:

54、

55、并且，

56、速度-压力形式的表述如下：

57、

58、进一步地，本发明用于提高工业仿真软件线弹性求解精度的数值方法步骤s4中所述时间离散化，包括：

59、热问题和力学问题的时间离散化基于有限差分方法，近似时间导数；

60、应用θ-格式原则，对于一个足够平滑的标量、向量或张量函数b，在考虑两个时间点τ和t＝τ+dt时，其在时间点t处的时间导数通过以下表达式近似：

61、

62、将上述方程应用于热问题和力学问题得到以下离散化的变分表述：

63、

64、

65、

66、进一步地，本发明用于提高工业仿真软件线弹性求解精度的数值方法步骤s5中所述空间离散化，包括：

67、(ptτ,t)、和的空间离散化由一个称为th的四边形网格给出，其特征为：

68、由n个节点(si)组成的集合：

69、由nh个六面体组成的集合

70、每个六面体的八个顶点的索引集合为hl,l＝0,...,nh-1；

71、总几何域

72、由nq个四边形组成的集合构成了几何域ωh的边界

73、每个四边形ql，l＝0,...,nq-1，的四个顶点的索引集合为

74、四边形网格th还满足与理论边界相关的几何符合性要求；不同前表面的四边形ql,l＝0,...,nq-1的顶点必须属于而分隔三个表面和以及两个表面和pour i＝0,1,2的曲线必须由这些四边形的边符合性地构成；

75、对于每个六面体hl,l＝0,...,nh-1，定义一个双射的几何变换flh:c→hl，将顶点为c0,...,c7的单位立方体映射到自身，该变换由以下公式表示：

76、

77、或者

78、n0(ξ0,ξ1,ξ2)＝(1-ξ0)(1-ξ1)(1-ξ2),n1(ξ0,ξ1,ξ2)＝ξ0(1-ξ1)(1-ξ2)；

79、n2(ξ0,ξ1,ξ2)＝ξ0ξ1(1-ξ2),n3(ξ0,ξ1,ξ2)＝(1-ξ0)ξ1(1-ξ2)2；

80、n4(ξ0,ξ1,ξ2)＝(1-ξ0)(1-ξ1)ξ2,n5(ξ0,ξ1,ξ2)＝ξ0(1-ξ1)ξ2；

81、n6(ξ0,ξ1,ξ2)＝ξ0ξ1ξ2,n7(ξ0,ξ1,ξ2)＝(1-ξ0)ξ1ξ2。

82、其中，avec、nk(ξ0,ξ1,ξ2),k＝0,...,7分别表示与点ck相关的形状函数，对于任意的k,m＝0,...,7，有

83、对于每个四边形ql,l＝0,...,nq-1，定义一个双射的几何变换flq:sq→ql，将单位正方形sq映射到ql中：

84、

85、或者

86、nq0(ξ0,ξ1)＝(1-ξ0)(1-ξ1),nq1(ξ0,ξ1)＝ξ0(1-ξ1)；

87、nq2(ξ0,ξ1)＝ξ0ξ1,nq3(ξ0,ξ1)＝(1-ξ0)ξ1；

88、其中，nqk(ξ0,ξ1),k＝0,...,3分别表示与点相关的形状函数；对于0到3范围内任意的k和m，有

89、进一步地，本发明用于提高工业仿真软件线弹性求解精度的数值方法步骤s6中所述数值方法的实现，包括：

90、(1)热传导问题的数值公式

91、通过有限元方法，由(ptτ,t)导出的数值热传导问题(pthτ,t)可以表述如下：

92、

93、由于问题(pthτ,t)是非线性的，通过应用牛顿-拉弗森算法来解决，该算法的目标是以递归方式确定收敛于解tht的函数序列具体如下所示：

94、

95、其中，表示以下数值问题(pthτ,t)(k)的解：

96、

97、并且，因此，定义热增量向量热残差向量和热刚度矩阵

98、

99、

100、

101、从而，解决数值问题(pthτ,t)(k)等效于解决线性系统：kkδtk＝-fk；

102、(2)速度形式下的力学问题的数值表述-

103、由导出的力学问题的数值速度形式化问题通过有限元方法表示如下：

104、

105、由于问题是非线性的，应用牛顿-拉弗森算法来解决，该算法的目标是以递归方式确定收敛于解vht的函数序列具体如下所示：

106、

107、其中，表示以下数值问题的解：

108、

109、因此，通过以下方式定义速度的块增量向量块速度残差向量以及块力学刚度矩阵

110、

111、

112、

113、从而，解决数值问题等效于解决线性系统：kkδvk＝-fk；

114、(3)速度-压力形式下的力学问题的数值表述

115、关于速度-压力形式下的力学问题采用无稳定项q1/q1形式求解，基于有限元方法，由推导而来的速度-压力形式的数值力学问题表示如下：

116、

117、由于问题是非线性的，应用newton-raphson算法来解决，该算法是通过迭代地确定函数列使其收敛到解(vht,pht)，迭代过程如下：

118、

119、其中，是以下数值问题的解：

120、

121、该条件下，

122、

123、

124、因此，通过块定义速度-压力增量向量速度-压力残差向量以及速度-压力块刚度矩阵

125、

126、

127、

128、

129、

130、

131、

132、从而，解决数值问题等效于解决线性系统：kkδvpk＝-fk。

133、此外，本发明还涉及上述用于提高工业仿真软件线弹性求解精度的数值方法在工业仿真软件设计开发中的用途。

134、本发明还提供了一种工业仿真软件设计系统，本工业仿真软件设计系统中内置了上述用于提高工业仿真软件线弹性求解精度的数值方法。

135、最后，本发明还提供了一种计算机可读存储介质，所述存储介质上存储有计算机程序，所述程序被处理器执行时实现上述用于提高工业仿真软件线弹性求解精度的数值方法的步骤。

136、需要指出的是，在有限元方法中，除了q1线性元素(又称为线性元素)，还存在q2线性元素(又称为二次元素)。q2元素使用二次多项式来逼近解的形状，相比于q1元素的线性逼近，q2元素能够提供更高的逼近精度。两者的区别和不同主要体现在以下几个方面：

137、1、形状函数：q1元素使用线性形状函数逼近解的形状，而q2元素使用二次形状函数逼近解的形状。这意味着q2元素在每个单元内部的逼近精度更高。

138、2、自由度：q1元素的自由度(节点数)较少，而q2元素的自由度较多。q1元素在每个单元内有一个节点，而q2元素在每个单元内有多个节点，从而提供更多的自由度来逼近解。

139、3、精度：由于q2元素的高阶逼近，相对于q1元素，它可以提供更高的数值精度。这对于某些问题或要求更高精度的应用可能是重要的。

140、4、计算复杂度：由于q2元素的自由度更多，因此它的计算复杂度相对较高，需要更多的计算资源和计算时间。

141、选择q1元素还是q2元素取决于具体问题的要求和性质。对于简单几何形状或对精度要求不高的问题，q1元素可能已经足够。相比于q2元素，q1元素有以下几个优点：

142、1、计算效率：由于q1元素的自由度(节点数)较少，相对于q2元素，它的计算复杂度较低。这意味着q1元素在相同计算资源下可以更快地进行求解，适用于大规模问题或计算资源有限的情况。

143、2、网格生成：q1元素相对于q2元素更容易生成。在生成复杂几何形状的网格时，q1元素通常比q2元素更简单且更易于控制，能够提供更好的网格质量。

144、3、稳定性：由于q1元素的逼近是线性的，它在某些情况下可能更稳定。对于某些非线性问题或存在潜在数值振荡的问题，q1元素可能比q2元素更可靠。

145、4、存储需求：由于q1元素的自由度较少，它需要的存储空间相对较小。这对于存储大规模问题的系数矩阵和向量等数据是有利的。

146、综上，q1元素在计算效率、网格生成、稳定性和存储需求方面具有一些优势。因此，在处理简单几何形状、计算资源有限或对计算效率要求较高的问题时，q1元素可能是一个更好的选择。

147、综上，本发明用于提高工业仿真软件线弹性求解精度的数值方法具有以下特点：

148、1、基于速度-压力形式的新型数值模型：本发明方法描述了一个新颖的速度-压力形式数值模型，该模型在特定问题领域或特定条件下具有优越性能。

149、2、新的数值算法和求解技术：本发明涉及新的数值算法和求解技术，用于解决速度-压力形式下的数学模型，这些算法和技术可包括数值稳定化方法、网格适应性技术、高效的线性方程组求解器等。

150、3、创新的应用领域或问题：本发明描述了将速度-压力形式应用于特定领域或问题的新颖方法，包括不可压缩流体流动、结构力学、固体-流体耦合等领域，或是针对特定类型的复杂几何体或非线性材料的问题。

151、4、数值模拟精度和效率的提升：本发明提供了提高数值模拟精度和效率的新的速度-压力形式方法，包括更准确的压力解、稳定的数值计算、更高的计算效率或更精细的物理过程描述等方面。

152、与现有的速度求解方式相比，本方法求解方式具有以下优点：

153、1、耦合精度：速度-压力形式可以更准确地描述速度场和压力场之间的耦合关系。这种耦合性可以在涉及不可压缩流体流动、多相流或其他需要同时考虑速度和压力的问题中提供更准确和可靠的解决方案。

154、2、压力稳定性：速度-压力形式在处理不可压缩流体问题时，通常能够提供更稳定的压力解。传统的速度形式在处理不可压缩流体时可能会导致压力震荡或数值不稳定，而速度-压力形式可以通过稳定化技术解决这些问题。

155、3、网格适应性：速度-压力形式通常能够更好地适应不同类型的网格和几何形状。这使得它在处理复杂几何体、非结构化网格或需要自适应网格划分的问题时更具优势。

156、4、数值效率：尽管速度-压力形式在某些方面相对复杂，但它可以提供更高的数值效率。这意味着在给定的计算资源下，速度-压力形式可以提供更精确的结果或更快的计算速度。

157、5、应用广泛性：速度-压力形式在流体力学、结构力学、石油工程、地下水模拟等领域中得到广泛应用。因此，将速度-压力形式作为创新点可以为这些领域提供改进的数值方法和解决方案。