基于分区段分析及非线性方程组求解的FPC接触变形数学建模方法

：本发明归属于电子工程领域，专注于开发用于预测柔性电路板(flexibleprinted circuit，简称fpc)接触弯曲形态的数学模型。具体而言，本发明提出了基于分区段分析及非线性方程组求解的fpc接触弯曲形态数学建模方法，旨在提高fpc设计的准确性和效率。

背景技术

0、
背景技术：

1、随着电子工程领域的快速发展，尤其是在柔性电路板(fpc)的应用方面，对于高效、精确的弯曲形态预测技术的需求日益增长。fpc以其独特的柔性和轻薄特性，在现代电子产品设计中扮演着至关重要的角色。它被广泛应用于各种高端电子设备，包括但不限于智能穿戴设备、智能手机、医疗设备以及航空航天器材，其中对fpc的性能要求尤为严苛。准确预测fpc在实际使用中的弯曲行为对于确保这些产品的可靠性和耐用性至关重要。

2、在现有技术中，有限元方法(fem)是分析fpc弯曲性能的常用手段。然而，该方法面临几个显著的局限性。首先，fem的操作过程复杂且耗时，需要由具备高度专业知识的工程师执行，这在一定程度上限制了其在快速产品开发周期中的应用。其次，fem在处理大规模或复杂模拟时的计算效率较低，这不仅增加了设计成本，也延长了产品从概念到市场的时间。此外，在处理特别复杂的fpc变形情况时，有限元方法(fem)的另一个挑战是其分析过程可能难以收敛。复杂的fpc变形往往涉及多变的几何形态和复杂的应力分布，这可能导致计算过程中出现数值不稳定性，使得fem分析难以在合理时间内达到准确的解，甚至出错。这种计算上的不确定性不仅增加了分析的复杂度，而且可能导致分析结果的不可靠性，从而影响设计的决策过程。因此，在处理复杂的fpc接触变形问题时，发明更加稳定且能够有效收敛的预测方法变得尤为重要。

3、鉴于这些挑战，亟需新型的数学模型，用于fpc的接触弯曲形态预测。

技术实现思路

0、
技术实现要素：

1、本发明涉及分区段分析及非线性方程组求解的fpc接触变形数学建模方法，该方法通过将fpc与其他部件的接触点作为分界点，将fpc进行分区段，在每个区段内，建议fpc弯曲曲率与其长度的线性关系，联合多个已知和未知的条件，建立非线性方程组，并基于雅可比矩阵迭代法对其进行求解，最终准确预测fpc接触后的变形曲线，为fpc的设计和制造提供了有力且高效的工具；以解决现有技术中使用的限元方法操作过程复杂且耗时，需要由具备高度专业知识的工程师执行，处理大规模或复杂的模拟时计算效率较低，分析过程可能难以收敛的技术问题。

2、为实现上述目的，本发明采用了如下技术方案：

3、基于分区段分析及非线性方程组求解的fpc接触变形数学建模方法，其特征在于，包含以下步骤：

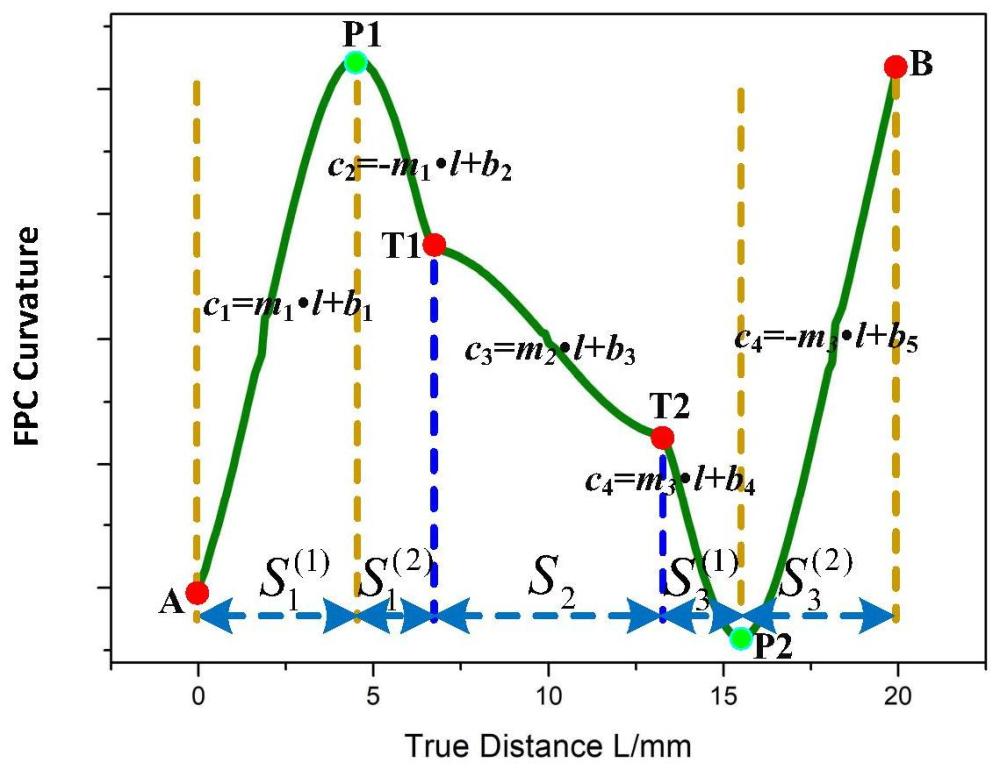
4、s1、基于有限元工具，对相应的fpc接触弯曲形态进行建模仿真分析，并获取其曲率变化与fpc沿长度方向的距离的关系；

5、s2、以接触点位置为界限，将曲率的变化趋势曲线进行分区段；

6、s3、在不同区段内，将fpc的曲率与沿着fpc长度的变化趋势进行线性化；

7、s4、将不同区段内的fpc参数联合成一个非线性方程组；

8、s5、对该非线性方程组进行求解，获得确定fpc接触变形所需的一系列参数；

9、s6、根据非线性方程组的求解结果，对fpc接触后的变形形状进行计算。

10、所述步骤s2中，具体包括以下步骤：

11、s2.1、根据接触点，将曲率的变化趋势曲线进行分区段；

12、s2.2、观察同一区段内，fpc的曲率变化是否单一，如果不单一，则继续进一步划分，确保在每一个小区段内，曲率随沿着fpc长度的变化趋势是单调递增或单调递减。

13、所述步骤s3中，具体包括以下步骤：

14、s3.1、在每一个小区段内，将fpc曲率与沿着fpc长度的关系进行线性化，会产生斜率和截距这些未知数；

15、s3.2、在以接触点为界限所确定大区段内，认定所有的小区段内的fpc曲率与沿着fpc长度的关系的斜率的绝对值是相等的。

16、所述步骤s4中，具体包括以下步骤：

17、s4.1、在以接触点为分界点的大区段内，将其两端点的x，y坐标差、切线角之差以及整个fpc曲线的两端点的x，y坐标差、切线角之差作为已知条件；

18、s4.2、将每个区段内的fpc曲率变化曲线的斜率、截距，接触点的具体坐标以及以接触点为分解点的各个区段内fpc的长度作为未知数，联立成一个非线性方程组；

19、所述步骤s5中，具体包括以下步骤：

20、s5.1、对于相应的复杂的非线性方程组的求解，主要基于雅可比矩阵迭代法进行求解，求解过程需要进行分段迭代，以确保相应的迭代过程可以搜索到附近的正确解；

21、s5.2、若接触变形过大，则将所接触部件的位置进行分段分析，逐步达到指定位置，完成最终fpc接触形状的分析。

22、与现有技术相比，本发明有益效果如下：

23、本发明提出了创新的方法，通过数学模型来精确地预测柔性电路板(fpc)在各种接触条件下的形变特性。这项技术对于改善fpc的设计和生产过程具有重要意义，能够显著提升其效能与可靠度。它为工程师和设计师在多个行业领域提供了一个强大的工具，使他们能够更准确地掌握和调控fpc的弯曲特性，进而在提升电子产品的整体性能和可靠性方面取得显著成效。

24、本发明的数学模型操作简便，计算速度快，准确性高，适用于快速设计迭代和原型开发。它降低了对操作人员的专业技能要求，使得更广泛的工程师和设计师可以直接应用于fpc的设计和分析中。这不仅有助于降低产品开发的时间和成本，还提升了产品设计的可靠性和创新性。

技术特征：

1.基于分区段分析及非线性方程组求解的fpc接触变形数学建模方法，其特征在于，包含以下步骤：

2.根据基于分区段分析及非线性方程组求解的fpc接触变形数学建模方法，其特征在于，所述步骤s2中，具体包括以下步骤：

3.根据基于分区段分析及非线性方程组求解的fpc接触变形数学建模方法，其特征在于，所述步骤s3中，具体包括以下步骤：

4.根据基于分区段分析及非线性方程组求解的fpc接触变形数学建模方法，其特征在于，所述步骤s4中，具体包括以下步骤：

5.根据基于分区段分析及非线性方程组求解的fpc接触变形数学建模方法，其特征在于，所述步骤s5中，具体包括以下步骤：

技术总结
本发明涉及基于分区段分析及非线性方程组求解的FPC接触变形数学建模方法，用于分析柔性电路板(FPC)在与其他零部件接触的情况下的变形；核心步骤包括：将FPC基于接触点划分为不同的区段；对不同FPC区段内，将FPC的曲率与沿着FPC表面路径的长度的关系进行线性化，同时得到一系列未知数，如线性关系中的斜率和截距；另外，对于接触点的具体坐标，以及每个FPC在不同区段内的长度，也作为需要求解的未知参数；已知的关系有不同区段两端的坐标差值，角度差值，以及不同区段首尾连接点处的曲率必须相等；同时运用雅可比矩阵迭代法和尺寸迭代法，对所有未知数进行求解，最终得到所需要求解的FPC与其他零部件不同接触条件下的变形曲线。

技术研发人员：孟龙晖,王华,张浩,洪荣晶
受保护的技术使用者：南京工业大学
技术研发日：
技术公布日：2024/3/24