一种基于物理信息神经网络的多层介质电磁计算方法

本发明涉及计算电磁学领域，具体涉及一种基于物理信息神经网络的多层介质电磁计算方法。

背景技术：

1、麦克斯韦方程是电磁学领域一组重要的偏微分方程，它描述了电场、磁场与电荷密度、电流密度之间关系。目前麦克斯韦方程的求解主要依靠一些数值求解方法，如时域有限差分法（finite-difference time-domain, fdtd） 和有限元法(finite elementmethod, fem)等。但传统的数值求解方法有很大的局限性，主要表现在复杂几何区域的网格生成困难，计算消耗大以及算法复杂等。

2、近年来随着深度神经网络理论的快速发展，深度神经网络在计算机视觉, 自然语言处理和语音识别等众多领域取得了突破性的成果。最近学者们提出了一种物理信息神经网络（physics-informed neural networks，pinn）来求解偏微分方程。pinn将物理知识以偏微分方程残差的形式融入到神经网络的损失函数之中，与传统的数值求解方法相比，pinn无需划分网格，在多维问题中可避免维度增加引起的计算困难，与其他的神经网络方法相比，pinn的预测结果更加满足物理定律，需要的数据量更少。目前已有研究将 pinn 应用到麦克斯韦方程的求解。然而，在实际应用中，pinn 在模拟多层介质中的电磁传播时，其准确度有待提高。因此，提出一种能够计算多层介质中麦克斯韦方程的新型 pinn模型至关重要。

技术实现思路

1、为了使 pinn能够应用到多层介质中的电磁计算问题，本发明提供了一种基于物理信息神经网络的多层介质电磁计算方法。

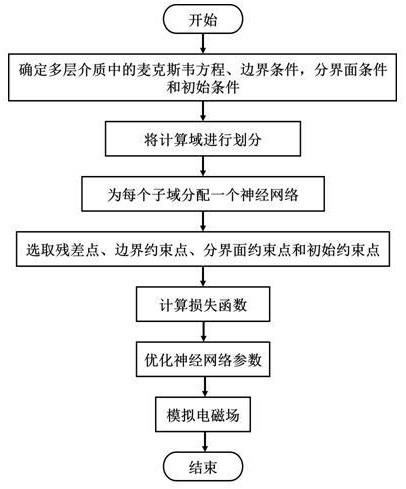
2、本发明通过以下技术方案实现：基于物理信息神经网络的多层介质电磁计算方法，包括以下步骤：

3、步骤一：确定计算域内的麦克斯韦方程、边界条件、分界面条件和初始条件；

4、步骤二：根据不同的介质区域，将计算域进行划分；

5、步骤三：为计算域内各个子域分配一个神经网络，建立电磁模型；

6、步骤四：在计算域内选取用于训练的残差点、边界约束点、分界面约束点和初始约束点；

7、步骤五：计算麦克斯韦方程残差损失、边界条件损失、分界面条件和初始条件损失，得到总损失函数；

8、步骤六：使用基于梯度下降的优化算法优化神经网络参数；

9、步骤七：根据得到神经网络模型，模拟计算域内的电磁场。

10、进一步的，所述步骤一中考虑的麦克斯韦方程，定义如下：

11、

12、其中 和 表示无量纲空间和时间坐标，是电场矢量，是磁场矢量。和  分别表示磁场和电场的初始条件约束， 和 分别表示电场和磁场的边界条件约束，表示计算域的边界。是磁导率、 是介电常数，定义如下：

13、

14、其中  表示不同的介质区域。在相邻介质之间的分界面上有如下的电磁分界面条件：

15、

16、其中 和分别表示电场在分界面上的切向和法向分量，和分别表示磁场在分界面上的切向和法向分量。

17、进一步的，所述步骤二中对计算域进行划分。根据不同的介质区域，即不同的麦克斯韦方程参数，将计算域划分成个子域，使得各子域内麦克斯方程参数是固定的。其中表示计算域内介质的层数。

18、进一步的，所述步骤三中神经网络定义为 ，结构定义如下：

19、

20、其中，网络的输入 为时空坐标，为神经网络  的输出，表示所有可训练的神经网络参数，表示非线性激活函数，是 sigmoid、relu、tanh中的一种。

21、进一步的，所述步骤四中采用均匀抽样，随机抽样或拉丁超立方抽样方法在计算域内选取训练点，训练点包括残差点、边界约束点，分界面约束点和初始约束点。其中 表示残差点， 表示边界约束点， 表示分界面约束点， 表示初始约束点，是总的训练点数。进一步的，所述步骤五中的中的麦克斯韦方程损失、边界条件损失、分界面条件损失和初始条件损失采用如下的形式：

22、

23、其中， 和  为麦克斯韦残差方程，具体定义如下：

24、

25、其中， 为第 个神经网络的参数。 为神经网络的总数。、 和  分别表示在第  个子域内的残差点数、边界约束点数和初始约束点数。 表示分界面条件残差方程，具体定义如下：

26、

27、其中 和分别表示两个拟合相邻介质区域物理量的神经网络在分界面处的估计值。

28、进一步的，所述步骤六中使用基于梯度下降的优化算法优化各神经网络参数 ,其迭代更新步骤如下：

29、

30、其中 是第 个神经网络的参数在第  步时的参数。是损失函数对神经网络参数  的梯度，表示更新步长。

31、进一步的，对训练好的神经网络模型验证及测试，以达到高精度模拟多层介质中的电磁传播的目的。

32、与现有技术相比，本发明的有益效果：

33、(1)本发明提出的基于物理信息神经网络的多层介质电磁计算方法，与传统数值求解方法相比在一些问题上更具有优势，如无需网格划分、避免“维数灾难”以及易于对复杂集合区域进行求解等。

34、(2)本发明通过域分解的方法将 pinn模型成功应用到了多层介质中的电磁计算问题。通过在pinn的损失函数中增加分界面条件损失项，提高了在分界面处的预测准确度。

技术特征：

1.一种基于物理信息神经网络的多层介质电磁计算方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤一中的麦克斯韦方程，定义如下：

3.根据权利要求1或2所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤三中神经网络定义为 ，结构定义如下：

4.根据权利要求1或2所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤四中采用均匀抽样，随机抽样或拉丁超立方抽样方法在计算域内选取训练点，训练点包括残差点、边界约束点，分界面约束点和初始约束点；其中  表示残差点， 表示边界约束点， 表示分界面约束点， 表示初始约束点，是总的训练点数。

5.根据权利要求3所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤四中采用均匀抽样，随机抽样或拉丁超立方抽样方法在计算域内选取训练点，训练点包括残差点、边界约束点，分界面约束点和初始约束点；其中  表示残差点， 表示边界约束点， 表示分界面约束点， 表示初始约束点，是总的训练点数。

6.根据权利要求1或2或5所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤五中的麦克斯韦方程损失、边界条件损失、分界面条件损失和初始条件损失采用如下的形式：

7.根据权利要求3所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤五中的麦克斯韦方程损失、边界条件损失、分界面条件损失和初始条件损失采用如下的形式：

8.根据权利要求1或2或5或7所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤六中使用基于梯度下降的优化算法优化各神经网络参数 , 其迭代更新步骤如下：

9.根据权利要求3所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤六中使用基于梯度下降的优化算法优化各神经网络参数 , 其迭代更新步骤如下：其中 是第 个神经网络的参数在第  步时的参数；是损失函数对神经网络参数  的梯度，表示更新步长。

10.根据权利要求1或2或5或7或9所述的基于物理信息神经网络的多层介质电磁计算方法，其特征在于，所述步骤二对计算域进行划分，具体如下：根据不同的介质区域，即不同的麦克斯韦方程参数，将计算域划分成个子域，使得各子域内麦克斯方程参数是固定的；其中表示计算域内介质的层数。

技术总结
本发明公开了一种基于物理信息神经网络的多层介质电磁计算方法。所述方法包括：步骤一：确定计算域内的麦克斯韦方程、边界条件、电磁分界面条件和初始条件；步骤二：根据不同的介质将计算域进行划分；步骤三：为计算域内各个子域分配一个神经网络，建立电磁模型；步骤四：在计算域内选取用于训练的残差点、边界约束点、分界面约束点和初始约束点；步骤五：根据选取的训练点计算麦克斯韦方程残差损失、边界条件损失、分界面条件和初始条件损失，并计算总损失函数；步骤六：使用基于梯度下降的优化算法优化神经网络参数；步骤七：根据得到电磁模型，模拟计算域内的电磁场。本发明能够快速准确地计算多层介质中的麦克斯韦方程，模拟电磁传播。

技术研发人员：朴世元,王嫒娜,秦攀
受保护的技术使用者：大连理工大学
技术研发日：
技术公布日：2024/5/6