一种精确浮点除法的计算方法、装置、设备及介质与流程

本发明实施例涉及数据处理，尤其涉及一种精确浮点除法的计算方法、装置、设备及介质。

背景技术：

1、目前的浮点除法通常使用牛顿迭代法实现，把除法转换为同精度的常规计算。例如单精度fp32浮点除法采用单精度fp32的加减乘实现，采用这种方式虽然能够快速高效的获取计算结果，但是结果通常会存在误差。

2、基于此目前提出的改进措施是扩展到高精度计算，即做双精度fp64浮点除法，此时即使fp64的结果仍有1个最小精度单位的误差，但转换到fp32时误差可能已经消除，但是采用这种方式通常需要更高精度的计算单元，因此需要消耗更多资源。

技术实现思路

1、本发明实施例提供一种精确浮点除法的计算方法、装置、设备及介质，以实现在减少计算资源消耗的情况下获取精确的浮点除法结果。

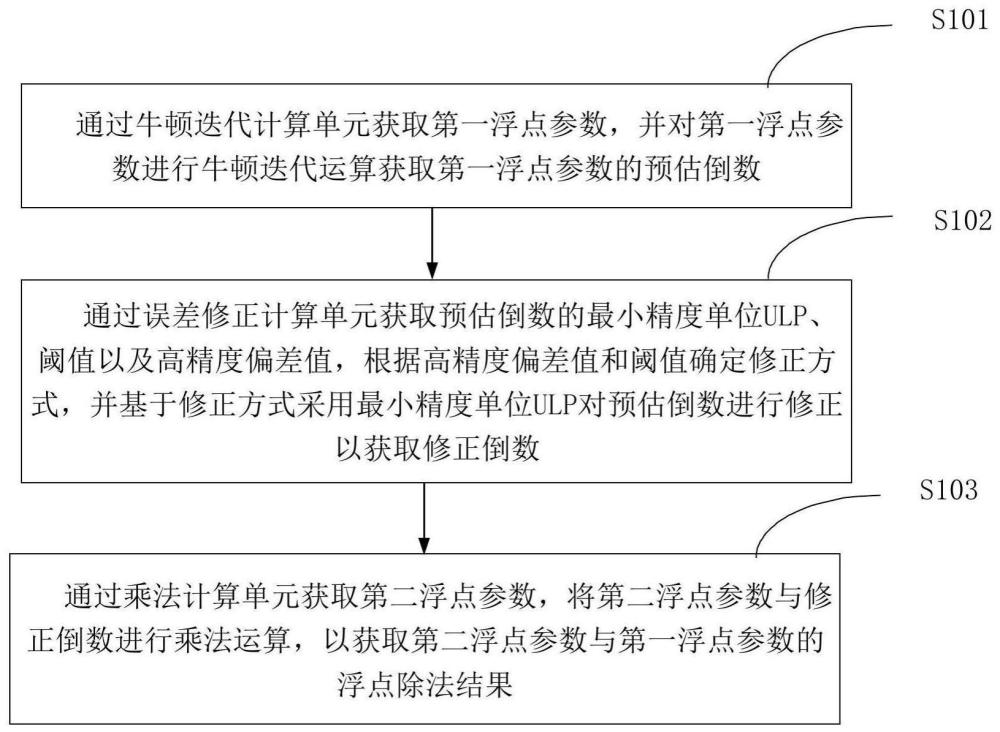
2、第一方面，本发明实施例提供了一种精确浮点除法的计算方法，应用于浮点除法计算系统，所述浮点除法计算系统包括牛顿迭代计算单元、误差修正计算单元和乘法计算单元，方法包括：

3、通过所述牛顿迭代计算单元获取第一浮点参数，并对所述第一浮点参数进行牛顿迭代运算获取所述第一浮点参数的预估倒数；

4、通过所述误差修正计算单元获取所述预估倒数的最小精度单位ulp、阈值以及高精度偏差值，根据所述高精度偏差值和所述阈值确定修正方式，并基于所述修正方式采用所述最小精度单位ulp对所述预估倒数进行修正以获取修正倒数；

5、通过所述乘法计算单元获取第二浮点参数，将所述第二浮点参数与所述修正倒数进行乘法运算，以获取所述第二浮点参数与所述第一浮点参数的浮点除法结果。

6、第二方面，本发明实施例提供了一种精确浮点除法的计算装置，包括：

7、预估倒数获取模块，用于通过牛顿迭代计算单元获取第一浮点参数，并对所述第一浮点参数进行牛顿迭代运算获取所述第一浮点参数的预估倒数；

8、修正倒数获取模块，用于通过误差修正计算单元获取所述预估倒数的最小精度单位ulp、阈值以及高精度偏差值，根据所述高精度偏差值和所述阈值确定修正方式，并基于所述修正方式采用所述最小精度单位ulp对所述预估倒数进行修正以获取修正倒数；

9、浮点除法结果获取模块，用于通过乘法计算单元获取第二浮点参数，将所述第二浮点参数与所述修正倒数进行乘法运算，以获取所述第二浮点参数与所述第一浮点参数的浮点除法结果。

10、本申请通过牛顿迭代计算单元获取到第一浮点参数的预估倒数后，会对牛顿迭代的计算结果采用高精度计算偏差，并将所获取的高精度偏差值转换为原始的低精度数据类型，并继续进行后续的计算，得到修正结果，因此在消除误差的同时仅是引入有限的高精度计算，从而在减少计算资源消耗的情况下获取到了精确的浮点除法结果。

技术特征：

1.一种精确浮点除法的计算方法，其特征在于，应用于浮点除法计算系统，所述浮点除法计算系统包括牛顿迭代计算单元、误差修正计算单元和乘法计算单元，方法包括：

2.根据权利要求1所述的方法，其特征在于，所述对所述第一浮点参数进行牛顿迭代运算获取所述第一浮点参数的预估倒数，包括：

3.根据权利要求1所述的方法，其特征在于，所述误差修正计算单元包括最小精度单位计算单元、阈值计算单元、高精度偏差计算单元和结果修正单元。

4.根据权利要求3所述的方法，其特征在于，所述通过所述误差修正计算单元获取所述预估倒数的最小精度单位ulp、阈值以及高精度偏差值，包括：

5.根据权利要求4所述的方法，其特征在于，所述计算数值1与所述高精度第二乘积结果的高精度偏差值之后，还包括：

6.根据权利要求3所述的方法，其特征在于，所述根据所述高精度偏差值和所述阈值确定修正方式，包括：

7.根据权利要求6所述的方法，其特征在于，所述基于所述修正方式采用所述最小精度单位ulp对所述预估倒数进行修正以获取修正倒数，包括：

8.一种精确浮点除法的计算装置，其特征在于，包括：

9.一种计算机设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，其特征在于，所述处理器执行所述程序时实现如权利要求1-7中任一项所述的方法。

10.一种计算机可执行指令的存储介质，其上存储有计算机程序，其特征在于，该程序被处理器执行时实现如权利要求1-7中任一项所述方法。

技术总结
本发明公开了一种精确浮点除法的计算方法包括：通过牛顿迭代计算单元获取第一浮点参数，并对第一浮点参数进行牛顿迭代运算获取第一浮点参数的预估倒数；通过误差修正计算单元获取预估倒数的最小精度单位ULP、阈值以及高精度偏差值，根据高精度偏差值和阈值确定修正方式，并基于修正方式采用最小精度单位ULP对预估倒数进行修正以获取修正倒数；通过乘法计算单元获取第二浮点参数，将第二浮点参数与修正倒数进行乘法运算，以获取第二浮点参数与第一浮点参数的浮点除法结果。对牛顿迭代的计算结果采用高精度计算偏差，将高精度偏差值转换为原始的低精度数据类型进行后续的计算，得到修正结果，在减少计算资源消耗的情况下获取到了精确的浮点除法结果。

技术研发人员：杨宏璋,张亚林
受保护的技术使用者：上海燧原智能科技有限公司
技术研发日：
技术公布日：2024/7/9