圆柱度误差评定方法及终端设备、存储介质

本发明涉及轴类零件形状误差检测领域，具体地涉及一种圆柱度误差评定方法及终端设备、存储介质。

背景技术：

1、圆柱度常用于衡量轴类零件形状误差的大小，其精度的高低直接影响产品的质量和使用寿命，目前在实验室和工厂环境条件中的圆柱度测量是在三坐标测量机上完成的，三坐标测量机一般是在直角坐标系下对圆柱表面进行采样，因此，利用三坐标测量机在直角坐标系下对圆柱度误差进行快速、准确的计算在工程应用中具有重要价值。

2、在三坐标测量机中，圆柱度误差评定的主要计算方法为最小二乘圆柱法(lsc)、该方法简单且容易实现，但不符合圆柱度误差的最小条件定义，并且该方法计算出的圆柱度误差值通常不是最小的。相比而言，最小区域圆柱法(mzc)是基于iso定义的圆柱度误差评估方法，其本质是找到包含所有测量点且具有最小半径差的同轴圆柱面，该方法得出的误差精度较高，能够获得更准确的圆柱度误差值，然而国际标准中并没有mzc的具体计算公式，因此mzc近年来受到了广泛的关注和研究。

3、目前报道了一系列的最小区域圆柱度误差评定方法，主要分为基于计算几何方法和基于智能优化算法两个方向。计算几何方法主要通过圆柱的几何特征计算最小区域圆柱体，而智能优化算法通过构建圆柱度误差的数学模型求解最小区域圆柱度误差，比如将粒子群算法、遗传算法、免疫算法等智能优化算法应用在圆柱度误差评定中。评定圆柱度误差的实质就是求测量点到理想轴线的半径差，利用圆柱轴线可以确定包围被测圆柱面的两个同轴圆柱面，两个同轴圆柱面的最小半径差即为最小区域圆柱度误差。因此，现有技术中的这两大类方法主要依赖于求解圆柱轴线方程参数从而评定圆柱度误差，普遍存在的问题是圆柱轴线方程较为复杂，难以获得准确的圆柱轴线而导致误差评定结果精度不高，或者智能优化算法需优化的圆柱轴线参数过多(四个或六个)而导致收敛速度慢，算法流程复杂，计算效率低，并且也有可能得不到最优解。

技术实现思路

1、本发明的目的是克服现有技术存在的问题，提供一种圆柱度误差评定方法及终端设备、存储介质，能够不依赖圆柱轴线方程，通过寻找最优旋转角度把圆柱度误差评定转换为圆度误差评定，无需寻找理想圆柱轴线方程，减少了优化参数个数，同时提高了计算精度和计算效率。

2、为了实现上述目的，本发明第一方面提供一种圆柱度误差评定方法，所述方法基于旋转投影和自适应粒子群优化，包括以下步骤：

3、s1、对圆柱零件表面沿轴线等间距采样测量，得到圆柱的多个截面数据作为圆柱测量数据；

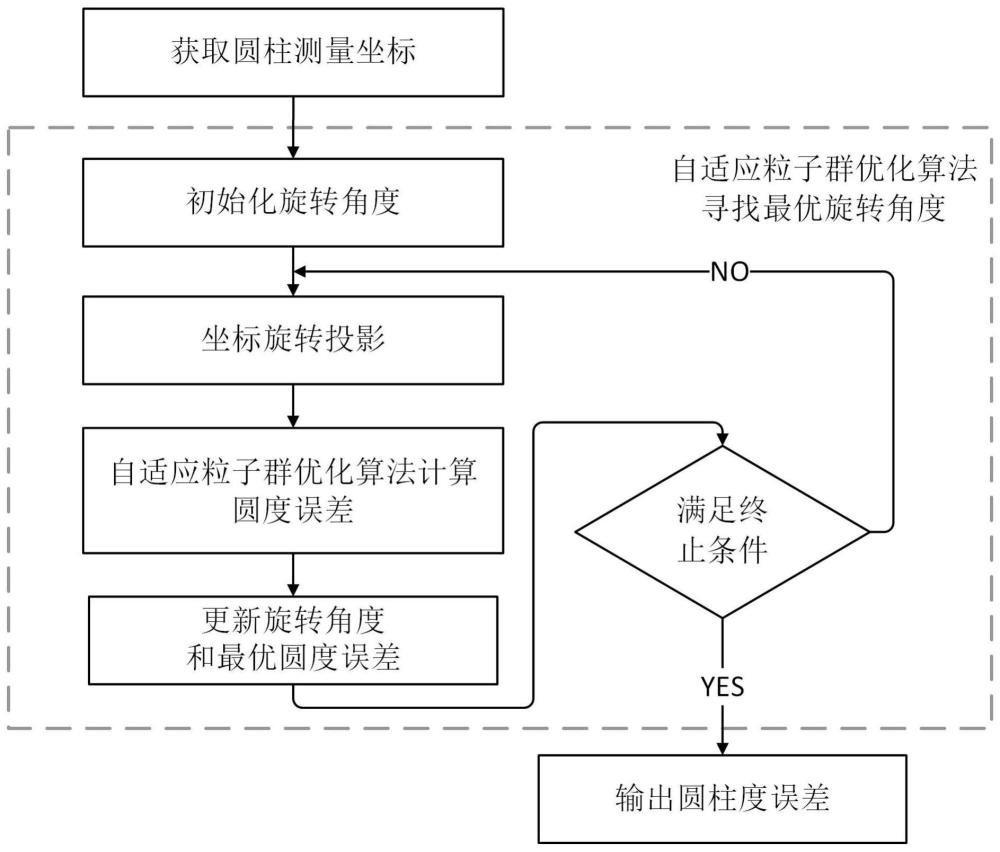
4、s2、自适应粒子群优化算法求解两个最优旋转角度α和β，求得的两个最优旋转角度对应的全局最优解gbest即为最小区域圆柱度误差，具体包括：

5、s21、设置自适应粒子群优化算法的参数，并通过halton序列获取粒子初始位置，粒子初始速度利用[0,1]的随机数进行设置，粒子位置表示圆柱坐标绕坐标系x轴和y轴的两个旋转角度α和β；

6、s22、将圆柱测量数据根据粒子位置坐标变换为新的圆柱坐标，然后将新的圆柱坐标数据投影到三坐标测量机坐标系xoy面上得到投影圆坐标数据；

7、s23、根据投影圆坐标数据，利用自适应粒子群优化算法计算投影圆坐标的最小区域圆度误差得到单次圆度误差最优解g1best；

8、s24、得到的最优解g1best作为当前粒子位置对应的适应度值，选择每个粒子当前最小的适应度值作为当前每个粒子的个体最优解pbest，对应的粒子作为当前每个粒子的个体最优解，选择全部粒子中最小的适应度值作为当前全局最优解gbest，对应的粒子作为当前全局最优解，每次迭代得到的pbest和gbest都保存，以便用于下一次迭代时进行更新；

9、s25、根据每个粒子的适应度值计算调整当前惯性权重值ω，并且根据当前全局最优解gbest和每个粒子的个体最优解pbest更新每个粒子的速度和位置；

10、s26、判断终止条件，迭代次数是否满足最大迭代次数t，如果满足则终止计算，最终得到的全局最优解gbest对应的两个旋转角度为两个最优旋转角度，输出全局最优解gbest；如果不满足，则返回步骤s22，迭代次数加1。

11、优选地，步骤s2中，在寻找两个最优旋转角度时，两个旋转角度为粒子群优化目标函数的自变量参数，根据旋转角度使得圆柱轴线与坐标系z轴无限接近平行时，此时可以将三维圆柱坐标投影为二维圆坐标，并且投影计算得到的最小区域圆度误差是最准确且最小的，所以优化目标函数得到的适应度值为当前两个旋转角度对应的投影坐标的最小区域圆度误差的最小值。所述自适应粒子群优化算法中寻找两个最优旋转角度的适应度值h(α,β)的计算公式如下：

12、h(α,β)＝min(g)

13、式中：α和β分别为圆柱坐标绕三坐标测量机坐标系x轴和y轴的两个旋转角度，min(g)为利用自适应粒子群优化算法计算得到的最小区域圆度误差的最小值。

14、本发明第二方面提供一种圆柱度误差评定终端设备，包括处理器、存储器以及存储在所述存储器中并在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现圆柱度误差评定方法的步骤。

15、本发明第三方面提供一种机器可读存储介质，该机器可读存储介质上存储有指令，该指令用于使得机器执行本申请上述圆柱度误差评定方法的步骤。

16、通过上述技术方案，本发明具有以下有益效果：(1)不依赖求解圆柱轴线方程参数来进行圆柱度误差评定，而是通过自适应粒子群优化算法寻找圆柱坐标绕三坐标测量机坐标系x轴和y轴的两个最优旋转角度，将三维圆柱坐标正确旋转投影为二维圆坐标，使得圆柱度误差转换为圆度误差，进行降维优化，无需计算复杂的圆柱轴线方程，很大程度上降低了计算难度；(2)本发明利用两次自适应粒子群优化算法分别寻找两个最优旋转角度和计算最小区域圆度误差，显著提高了寻找两个最优旋转角度和计算最小区域圆度误差的计算精度和计算效率，并且每次仅需优化两个参数，而其他利用pso、apso等智能优化算法评定圆柱度误差方法中，需要根据圆柱轴线方程的参数确定所需优化的参数，一般为4个或者6个，相比之下，本发明大幅减少了优化参数的个数，极大的降低了自适应粒子群优化算法求解的难度，同时自适应惯性权重的引入降低了粒子群优化算法陷入局部最优的可能性，提高了算法的可靠性；(3)本发明能够大幅提升圆柱度误差评定的计算精度和效率，对于微纳米三坐标测量机中圆柱度误差的实时、准确评定具有重要价值。

技术特征：

1.一种圆柱度误差评定方法，其特征在于，所述方法基于旋转投影和自适应粒子群优化，包括以下步骤：

2.根据权利要求1中所述的方法，其特征在于，步骤s2中，所述自适应粒子群优化算法中寻找两个最优旋转角度的适应度值h(α,β)的计算公式如下：

3.根据权利要求1所述的方法，其特征在于，步骤s21中，通过halton序列初始化粒子位置，粒子初始速度利用[0,1]的随机数进行设置，公式如下：

4.根据权利要求1所述的方法，其特征在于，步骤s22中，所述将圆柱测量数据根据粒子位置坐标变换为新的圆柱坐标，然后将新的圆柱坐标投影到坐标系xoy面上得到投影圆坐标数据，变换公式如下：

5.根据权利要求1所述的方法，其特征在于，步骤s25中，所述根据每个粒子的适应度值计算当前惯性权重值ω的计算公式为：

6.根据权利要求1所述的方法，其特征在于，步骤s23中，所述利用自适应粒子群优化算法计算投影圆坐标的最小区域圆度误差包括以下过程：

7.根据权利要求6所述的方法，其特征在于，所述根据投影圆坐标数据和圆心坐标计算每个粒子的适应度值的计算公式为：

8.根据权利要求1-7中任一所述的方法，其特征在于，将被测圆柱零件放在三坐标测量机的工作台上，通过圆周线提取法进行测量。

9.一种圆柱度误差评定终端设备，其特征在于，包括处理器、存储器以及存储在所述存储器中并在所述处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现如权利要求1-8中任一项方法的步骤。

10.一种机器可读存储介质，该机器可读存储介质上存储有指令，该指令用于使得机器执行本申请上述权利要求1-8中任一项方法的步骤。

技术总结
本发明涉及轴类零件形状误差检测领域，具体公开了一种圆柱度误差评定方法及终端设备、存储介质，所述方法通过自适应粒子群优化算法找到以圆柱轴线为基准的圆柱坐标绕三坐标测量机坐标系X轴和Y轴的两个最优旋转角度，使得圆柱轴线与三坐标测量机坐标系Z轴平行，然后通过坐标变换将三维圆柱坐标旋转投影为二维圆坐标，最后再次利用自适应粒子群优化算法计算投影的二维圆坐标的最小区域圆度误差，此时两个最优旋转角度对应的投影坐标的最小区域圆度误差等同于最小区域圆柱度误差。该方案无需寻找理想圆柱轴线方程，减少了优化参数个数，同时提高了计算精度和计算效率。

技术研发人员：程荣俊,简合帮,张文龙,黄强先,李红莉,张连生
受保护的技术使用者：合肥工业大学
技术研发日：
技术公布日：2024/6/26