一种加筋圆柱壳静动力响应力学特性数值仿真方法

本发明涉及加筋圆柱壳静动力响应力学特性数值仿真，尤其涉及一种加筋圆柱壳静动力响应力学特性数值仿真方法。

背景技术：

1、加筋圆柱壳是由圆柱壳结构，肋条、桁条或框架等加强筋组成的整体结构，在加筋圆柱壳中，加强筋与圆柱壳可以共同承受径向外载、轴向和环切向的载荷，进而加强结构的力学性能。此外，由于具有轻质、比刚度高、良好的动静态性能等特点，加筋圆柱壳在航空航天、交通、土木、水工、海洋、核等众多领域都具有潜在的用途。因此，研究加筋圆柱壳的静动力学行为对于提高结构性能、确保安全性和可靠性具有重要意义。

2、当前，为了满足计算精度的需求，大部分研究方法通常需要对整个结构域进行离散化处理，包括厚度方向。然而这类建模方法往往存在较大的局限性，以目前发展较为成熟且广泛应用的有限元法为例，为了适应壳体结构面内尺寸远大于厚度方向尺寸的实际情况，避免剪切自锁、网格依赖等数值问题的出现，往往需要将计算域离散为更加精细的网格，以此来满足工程实际所需要的精度要求，这很大程度上增加了计算成本且降低了计算效率。除有限元法外，解析法也是一种热门方法，该方法通常能够提供准确的数学解，尤其是在问题的数学模型和方程可以清晰地建立和求解的情况下。解析法建立在数学和物理的严密理论基础上，使其具有高度的可靠性。对于一些简单和理想化的情况，解析法是非常有效的。但是，当问题的复杂性增加、非线性效应显著时，解析法可能会变得非常复杂且难以求解。因此，亟需提出一种计算成本较低且精度较高的加筋圆柱壳静动力响应力学特性数值仿真方法。

技术实现思路

1、本发明的主要目的在于提供一种加筋圆柱壳静动力响应力学特性数值仿真方法，旨在解决现有获取加筋圆柱壳静动力响应力学特性仿真方法计算成本高的技术问题。

2、为实现上述目的，本发明提供一种加筋圆柱壳静动力响应力学特性数值仿真方法，所述方法包括以下步骤：

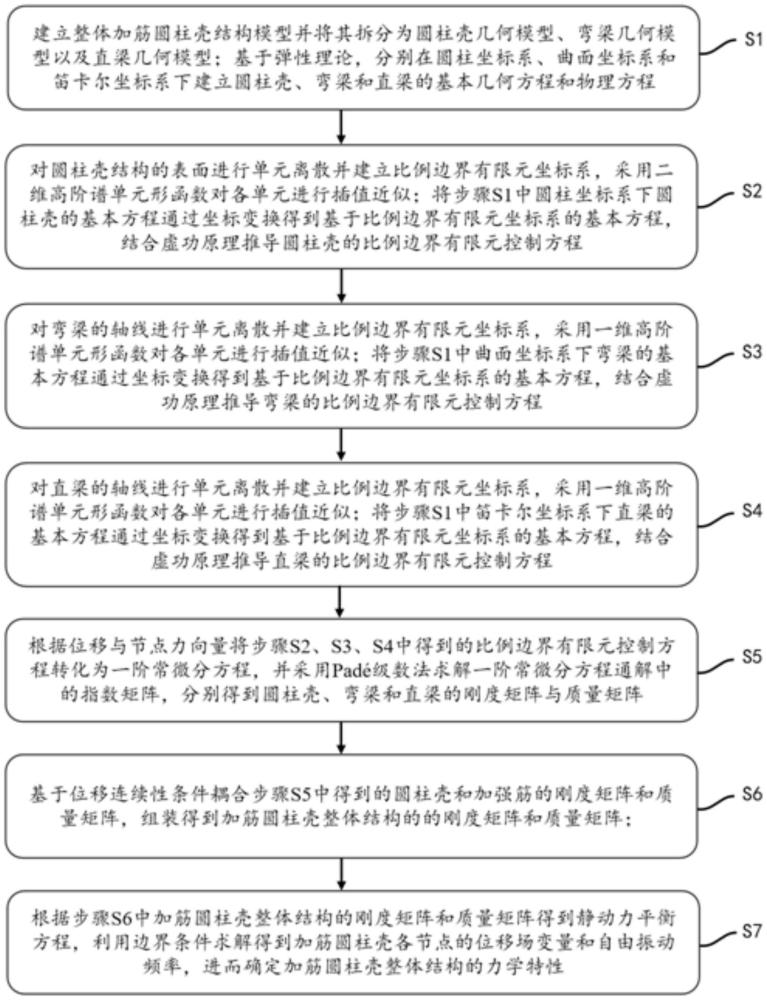
3、s1、建立整体加筋圆柱壳结构模型并将其拆分为圆柱壳几何模型、弯梁几何模型以及直梁几何模型；基于弹性理论，分别在圆柱坐标系、曲面坐标系和笛卡尔坐标系下建立圆柱壳、弯梁和直梁的基本几何方程和物理方程；

4、s2、对圆柱壳结构的表面进行单元离散并建立比例边界有限元坐标系，采用二维高阶谱单元形函数对各单元进行插值近似；将步骤s1中圆柱坐标系下圆柱壳的基本方程通过坐标变换得到基于比例边界有限元坐标系的基本方程，结合虚功原理推导圆柱壳的比例边界有限元控制方程；

5、s3、对弯梁的轴线进行单元离散并建立比例边界有限元坐标系，采用一维高阶谱单元形函数对各单元进行插值近似；将步骤s1中曲面坐标系下弯梁的基本方程通过坐标变换得到基于比例边界有限元坐标系的基本方程，结合虚功原理推导弯梁的比例边界有限元控制方程；

6、s4、对直梁的轴线进行单元离散并建立比例边界有限元坐标系，采用一维高阶谱单元形函数对各单元进行插值近似；将步骤s1中笛卡尔坐标系下直梁的基本方程通过坐标变换得到基于比例边界有限元坐标系的基本方程，结合虚功原理推导直梁的比例边界有限元控制方程；

7、s5、根据位移与节点力向量将步骤s2、s3、s4中得到的比例边界有限元控制方程转化为一阶常微分方程，并采用padé级数法求解一阶常微分方程通解中的指数矩阵，分别得到圆柱壳、弯梁和直梁的刚度矩阵与质量矩阵；

8、s6、基于位移连续性条件耦合步骤s5中得到的圆柱壳和加强筋的刚度矩阵和质量矩阵，组装得到加筋圆柱壳整体结构的的刚度矩阵和质量矩阵；

9、s7、根据步骤s6中加筋圆柱壳整体结构的刚度矩阵和质量矩阵得到静动力平衡方程，利用边界条件求解得到加筋圆柱壳各节点的位移场变量和自由振动频率，进而确定加筋圆柱壳整体结构的力学特性。

10、本发明的有益效果：

11、(1)本发明采用单元细分并结合sbfem基函数对加筋圆柱壳结构进行插值近似，进而实现将三维问题转换成二维平面的计算，实现将加筋圆柱壳仿真具体化呈现；

12、(2)本发明基于弹性理论、虚功原理和padé级数将静动力分析转换成求解矩阵方程，在降低计算量的同时提升计算精度计算效率，最终可高效获取加筋圆柱壳的力学特征。

技术特征：

1.一种加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，所述方法包括以下步骤：

2.如权利要求1所述的加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，在所述步骤s1中，建立整体加筋圆柱壳结构模型并将其拆分为圆柱壳几何模型、弯梁几何模型以及直梁几何模型；基于弹性理论，分别在圆柱坐标系(r,z,θ)、曲面坐标系(β,γ)和笛卡尔坐标系(x,y)下建立圆柱壳、弯梁和直梁的基本几何方程和物理方程；

3.如权利要求1所述的加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，在所述步骤s2中，对圆柱壳结构的表面进行单元离散并建立比例边界有限元坐标系(ξ,η,ζ)，采用二维高阶谱单元形函数[n(η,ζ)]对各单元进行插值近似的表达式为：

4.如权利要求1所述的加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，在所述步骤s3中，对弯梁的轴线进行单元离散并建立比例边界有限元坐标系(ξ,ζ)，采用一维高阶谱单元形函数[n(ζ)]对各单元进行插值近似的表达式为：

5.如权利要求1所述的加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，在所述步骤s4中，对直梁的轴线进行单元离散并建立比例边界有限元坐标系(ξ,η)，采用一维高阶谱单元形函数[n(η)]对各单元进行插值近似的表达式为：

6.如权利要求1所述的加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，在所述步骤s5中，根据位移与节点力向量{x(ξ)}＝{{u(ξ)} {q(ξ)}}t将步骤s2、s3、s4中得到的比例边界有限元控制方程统一转化为一阶常微分方程：

7.如权利要求1所述的加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，在步骤s6中，构造圆柱壳的刚度矩阵和加强筋的刚度矩阵基于位移连续性条件对矩阵进行耦合，建立加筋圆柱壳整体结构基于各节点位移和节点力的方程：

8.如权利要求1所述的加筋圆柱壳静动力响应力学特性数值仿真方法，其特征在于，步骤s7中，根据步骤s6中加筋圆柱壳整体结构的刚度矩阵和质量矩阵，得到静动力平衡方程

技术总结
一种加筋圆柱壳静动力响应力学特性数值仿真方法，该方法包括建立并拆分加筋圆柱壳对应的结构模型，基于弹性理论，分别在柱面坐标系、曲面坐标系和笛卡尔坐标系下建立圆柱壳、弯梁和直梁的基本几何方程和物理方程；采用高阶谱单元形函数分别对圆柱壳、弯梁和直梁进行插值近似，并通过坐标变换得到基于比例边界有限元坐标系的基本方程，结合虚功原理推导各结构的比例边界有限元控制方程；采用Padé级数进行矩阵指数运算，基于位移连续性条件对圆柱壳和加强筋进行耦合，得到加筋圆柱壳整体结构的刚度矩阵和质量矩阵；最后利用边界条件求解得到加筋圆柱壳各节点的位移场变量和自由振动频率，进而确定加筋圆柱壳整体结构的力学特性。

技术研发人员：黄楚豪,叶文斌,刘俊,徐强,姬晨曦,林皋
受保护的技术使用者：大连理工大学
技术研发日：
技术公布日：2024/8/1