粗粒土邓肯非线性抗剪强度指标均值及其方差的计算方法

本发明属于岩土工程领域，具体为粗粒土邓肯非线性抗剪强度指标均值及其方差的计算方法，采用全部大三轴试验数据进行回归计算，旨在提高岩土工程中粗粒土抗剪强度指标均值的计算精度，并解决其方差的估计问题。

背景技术：

1、粗粒土料具有取材方便、造价低、透水性好等优点，被广泛应用于道路、土石坝、填海造陆以及高填方机场等工程中。在这些工程建设中，填筑土料的抗剪强度将直接关系工程安全与投资，是十分重要的关键技术参数。

2、目前，确定土的抗剪强度指标不同规范并不相同。如《碾压式土石坝设计规范(sl274-2020)、(nb/t10872-2021)》建议对细粒土采用11组试验(每组4-6个围压)的小值平均值作为土体抗剪强度的标准值，《水利水电工程结构可靠性设计统一标准(gb5099-2013)》则建议采用0.1分位值作为土体抗剪强度的标准值。显然，对工程应用而言，土体抗剪强度指标的均值与方差(或标准差)同等重要。

3、目前，粗粒土的抗剪强度指标大多采用现场取散装样运至实验室内重新制样进行试验的办法确定。由于粗粒土料的最大粒径较大，往往需要用缩小粒径的材料进行试验，试验采用的最大粒径不大于三轴仪直径的1/5。一般情况下，材料试验组数不多，《碾压式土石坝设计规范(nb/t10872-2021)》规定粗粒土抗剪强度试验不少于6组，其抗剪强度指标采用小值平均值作为标准值推荐使用，故不再进行方差计算。抗剪强度指标小值平均值的具体计算是根据试验分组确定各组的邓肯非线性抗剪强度指标，然后统计确定小值平均值；也可以确定各围压下破坏状态莫尔圆心坐标与半径的小值平均值，再计算抗剪强度指标。这些方法的缺点在于确定中间量的样本偏少，导致统计量本身的误差偏大。

4、目前在涉及粗粒土工程的可靠度分析中，粗粒土抗剪强度方差多采用不同工程类似土料的统计值。这样处理显然对工程中任意一种土料土性参数的准确性把握有限。还没有见到直接根据一个工程粗粒土料试验的抗剪强度指标的均值及其方差进行边坡稳定、地基承载力等可靠度分析的报道。

5、解决以上问题的关键是改进粗粒土抗剪强度指标的计算方法。除提高粗粒土抗剪强度指标均值的计算精度外，还要确定抗剪强度指标的方差。

技术实现思路

1、本发明的目的在于提供一种粗粒土邓肯非线性抗剪强度指标均值与方差的计算方法，为确定粗粒土料抗剪强度设计标准值以及进行涉及粗粒土工程的边坡稳定、地基承载力等可靠度分析提供参数。

2、该方法不再对粗粒土的大三轴试验进行分组，将所有试验数据点作为一个整体，采用最小二乘法拟合邓肯非线性抗剪强度指标的平均值。但拟合残差显示其具有方差异性和相关性，并不满足最小二乘法的应用条件。为此，本发明提出了采用消除方差异性和相关性的广义最小二乘法，拟合邓肯非线性抗剪强度指标的均值并计算方差。结果表明，消除方差异性和相关性的广义最小二乘法得到的抗剪强度指标平均值与普通最小二乘法差别不大，但新方法强度指标的方差却有所降低。说明消除方差异性和相关性的广义最小二乘法对粗粒土邓肯非线性抗剪强度指标的估计更加精准。采用这一强度指标进行相关计算，能够更加准确地把握粗粒土工建筑物的安全性，提高其经济性。

3、本发明的技术方案是：

4、粗粒土邓肯非线性抗剪强度指标均值与方差的计算方法，包括如下步骤：

5、第一步：在粗粒土应力应变大三轴试验的基础上，形成粗粒土邓肯非线性抗剪强度最小二乘法拟合的数据集。

6、试验组数不少8组，每组4-6个围压等级。根据大三轴试验的破坏标准，确定每个试样在固定围压下σ3的破坏主应力差(σ1-σ3)f。据此计算每个试样破坏时的内摩擦角σ1、σ3为试样大小主应力，(σ1-σ3)f、(σ1+σ3)f分别为试样破坏时大小主应力差与和。形成拟合粗粒土邓肯非线性抗剪强度的数据对n为全部大三轴试验个数。

7、第二步：广义最小二乘法计算粗粒土邓肯非线性抗剪强度指标的均值与方差。

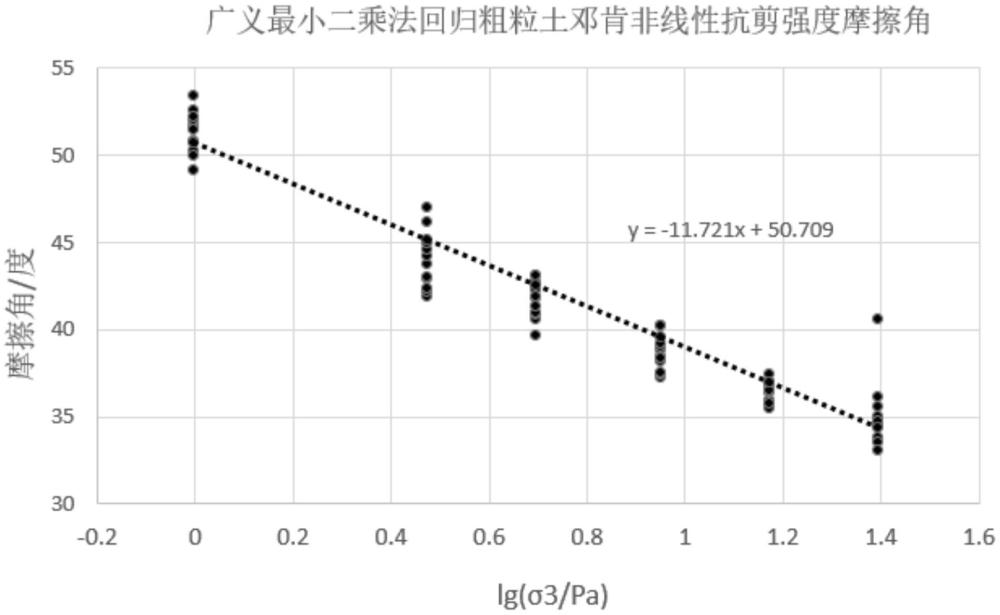
8、土的莫尔-库伦抗剪强度应用于粗粒土时，凝聚力c＝0，摩擦角随围压变化，以反映抗剪强度的非线性，σn为破坏面上正压力。邓肯提出粗粒土抗剪强度的摩擦角为

9、

10、式中，σ3为试样的小主应力，pa为一个大气压力；为邓肯方法抗剪强度指标，是待求的回归参数。

11、记lg(σ3/pa)＝x，

12、则回归方程为

13、y＝β0+β1x

14、根据第一步获得的试验数据，可形成n组回归数据点(xi,yi),i＝1,2,…,n。

15、最小二乘法回归分析使误差(也称残差)向量e＝y-xβ的长度之平方最小。因为最小二乘法回归邓肯非线性抗剪强度其残差具有方差异性与相关性，需要采用消除残差方差异性与相关性的广义最小二乘法计算粗粒土邓肯非线性抗剪强度指标均值与方差。计算公式如下：

16、回归参数均值采用估计

17、

18、回归参数的协方差矩阵为

19、

20、式中，为第i次试验的围压和摩擦角。t表示矩阵的转置。v为各围压下误差向量的协方差矩阵。σ2为整个误差向量的方差。

21、本发明的有益效果是：

22、本发明提高了粗粒土邓肯非线性抗剪强度指标的均值与方差的计算精度。摒弃了分组计算抗剪强度指标方法，将全部试验数据作为整体，采用广义最小二乘法拟合粗粒土抗剪强度的均值与方差。

23、经典最小二乘法拟合邓肯非线性抗剪强度时残差具有方差异性和相关性，违反了最小二乘法的使用条件。故提出了采用消除残差的方差异性和相关性的广义最小二乘法，求取粗粒土料邓肯非线性抗剪强度指标均值与方差的方法。

技术特征：

1.粗粒土邓肯非线性抗剪强度指标均值与方差的计算方法，其特征在于，包括如下步骤：

技术总结
本发明属于岩土工程领域，具体为粗粒土邓肯非线性抗剪强度指标均值及其方差的计算方法，旨在提高岩土工程中粗粒土抗剪强度指标均值的计算精度，并解决其方差的估计问题。本发明中，试验组数不少于8组、每组试验4‑6级围压的情况下，将全部数据作为整体，采用广义最小二乘法拟合粗粒土邓肯非线性抗剪强度指标的均值与方差。普通最小二乘法拟合粗粒土邓肯非线性抗剪强度指标存在残差的方差异性和相关性问题，不符合最小二乘的应用条件。本发明为工程设计中准确确定粗粒土抗剪强度指标的标准值，以及涉及粗粒土工程的可靠度分析奠定了基础。

技术研发人员：迟恒,迟世春,贾宇峰,邹德高
受保护的技术使用者：大连理工大学
技术研发日：
技术公布日：2024/10/21