一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法与流程

本发明涉及声波传感器，具体而言，涉及一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法。

背景技术：

1、声波谐振器是一种利用弹性波在固体介质中的传播和反射特性来实现的无源电子器件，适被用于速度传感器、温度传感器、力学传感器，尤其在射频通信、无损检测、医疗超声等领域已经广泛运用。声波谐振器的工作原理是利用材料压电效应，通过在材料表面电极上施加交流电来激发谐振器结构中的体声波或表声波，从而使得声波谐振器以特定的模态和频率进行振动。掌握弹性波在谐振器结构中的传播特性是表征声波谐振器工作性能的基础，弹性波的传播特性可以通过其频散关系来表征，即弹性波的频率与其传播波数的关系。通过确定声波谐振器中弹性波的频散关系，就可以决定声波谐振器的谐振频率、模态振型、声波速度等关键性能指标，从而为声波谐振器的设计以及工作模态、频率和波速选择提供指导。

2、一般而言，弹性固体中弹性波的频散关系可以通过显式代数关系表征，其频散关系可以通过常规的数值计算方法来求解显示代数关系的零点来确定。然而，声波谐振器由于其压电材料的力电耦合效应和器件结构的复杂性，其频散关系无法通过显示代数关系来表征，常常表现为隐式的复代数方程，因此难以通过常规的数值计算方法来确定方程的零点，因此，发展有效的数值方法来快速求解隐式复代数方程，从而确定声波谐振器中弹性波的频散关系是声波器件研究领域的一个难点问题。

3、目前，一些研究人员也发明了一些技术方法来确定声波器件中的频散关系，例如，南京航空航天大学申请了公开号为【cn105590025a】的发明专利《一种求解声波传感器中弥散曲线的数值方法》，他们通过计算弥散方程的模值，以及比较可能零点区间内模值比的收敛性从而确定了声波传感器中的弥散曲线。

4、虽然上述公开的数值方法能够求解由复弥散方程确定的声波传感器中的弥散曲线，但是实践表明，该模值收敛数值算法的计算效率较低，主要体现在：1)该技术方法求解频散曲线所对应的隐式复代数方程时，是通过比较搜索区间内复弥散方程的模值来判断该区间是否存在零点，所以需要对该搜索区间进行多个子区间划分，并计算每个子区间端点处复弥散方程的模值，使得每个搜根区间实际所需的计算数量显著增加；而在确定某个步长区间可能存在零点后，该技术方法还要通过比较复弥散方程的模值来进行收敛，同样需要对步长区间划分庞大的子区间，并不停迭代计算各个子步长点所对应的复频散方程的模值，这些搜根步骤大大增加了技术方法所需要的实际计算时间，导致技术方法效率低下；2)搜根区间所划分的子区间个数也会影响隐式复代数方程的求解精度，从而影响所确定的频散关系的精确度。

5、综上所述，仍然需要发展数值方法，来解决声波谐振器中弹性波频散关系无法被快速且精确求解的问题，进而掌握声波谐振器工作模态的振型及谐振频率。

技术实现思路

1、为了应对现有声波谐振器中弹性波频散关系求解效率低等问题，本发明公开了一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法。

2、本发明提供了一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，所述二维频散关系通过二维隐式复代数方程f(k,ω)＝0表征，求解出二维隐式复代数方程f(k,ω)＝0的零点，利用零点在频率-波数平面上组成声波谐振器中弹性波的二维频散关系，具体包括：

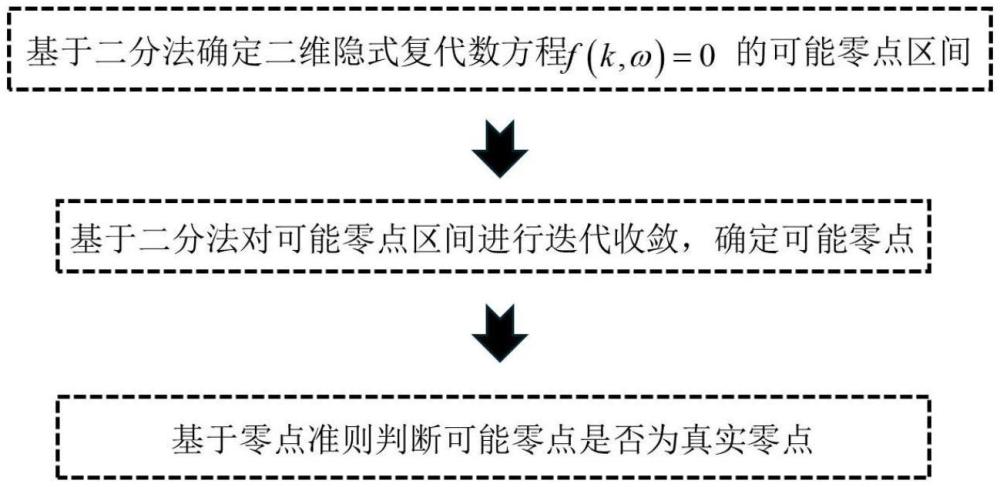
3、步骤s1、基于二分法确定二维隐式复代数方程f(k,ω)＝0的可能零点区间；

4、步骤s2、基于二分法对可能零点区间进行迭代收敛，确定可能零点；

5、步骤s3、对比可能零点和步骤s1中可能零点区间左端点的复频散方程函数的模值，判断是否为真实零点。

6、在一些实施例中，在步骤s1中，具体包括：

7、二维隐式复代数方程的根存在于平面空间(k,ω)中，此时传播波数为纯实数或者纯虚数；

8、二维隐式复代数方程的解为平面空间)k,ω)中的曲线，选择固定频率或者波数的直线，可与二维隐式复代数方程的解曲线相交于一点，通过线单元对固定频率或者波数的直线进行分区间搜索；

9、当固定频率为ω0进行线单元扫描搜根时，函数f(k,ω0)表示为f(k,ω0)＝a+bi，其中，a和b分别表示函数值的实部和虚部，i表示虚数单位；

10、令g(k,ω0)＝a+b，求解f(k,ω0)＝a+bi＝0的零点，等效为求解g(k,ω0)＝a+b＝0的零点；

11、选取步长划分搜根区间，计算函数g(k,ω0)＝a+b在每个搜根区间两端端点的函数值，如果两端端点的函数值异号，则该搜根区间存在可能零点，称之为可能零点区间；如果该搜根区间两端端点的函数g(k,ω0)＝a+b的函数值同号，则对下一个搜根区间两端端点的函数值进行计算，直至出现搜根区间两端端点函数值异号，确定该搜根区间为可能零点区间。

12、在一些实施例中，在步骤s2中，具体包括：

13、步骤s21、确定可能零点区间后，计算可能零点区间的中间点和左端点处函数g(k,ω0)＝a+b的值；

14、步骤s22、如果左端点的函数值与中间点的函数值异号，则将左端点与中间点作为新迭代区间；如果左端点的函数值与中间点的函数值同号，则将中间点与原区间右端点作为新迭代区间；

15、步骤s23、计算新迭代区间中间点和左端点的函数值，重复步骤s22确定下一个新迭代区间；重复上述过程，直至新迭代区间中间点与左端点的差值小于10-16，表示迭代收敛结束，最后得到的迭代区间的中间点为函数g(k,ω0)＝a+b的可能零点。

16、在一些实施例中，在步骤s3中，具体包括：

17、g(k,ω0)＝a+b＝0的可能零点包括假零点和真实零点；

18、比较搜根区间左端点的函数f)kl,ω0)的模值与可能零点处的函数f)k0,ω0)模值的比值；

19、若比值趋近于无穷大，则该可能零点为真实零点；

20、若比值小于实数m,则该可能零点为假零点。

21、本发明的有益效果在于：

22、本发明公开了一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，从而确定弹性波在谐振器结构中传播时其频率和传播波数间的定量关系，在得到频散关系后，可以进一步确定声波谐振器的模态振型和谐振频率，从而决定声波谐振器实际工作时的模态和频率选择，为声波器件的结构设计和应用提供参考。

技术特征：

1.一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，其特征在于，所述二维频散关系通过二维隐式复代数方程f(k,ω)＝0表征，求解出二维隐式复代数方程f(k,ω)＝0的零点，利用零点在频率-波数平面上组成声波谐振器中弹性波的二维频散关系，具体包括：

2.根据权利要求1所述的一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，其特征在于，在步骤s1中，具体包括：

3.根据权利要求2所述的一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，其特征在于，在步骤s2中，具体包括：

4.根据权利要求3所述的一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，其特征在于，在步骤s3中，具体包括：

技术总结
本发明提供了一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，所述二维频散关系通过二维隐式复代数方程f(k,ω)＝0表征，求解出二维隐式复代数方程f(k,ω)＝0的零点，利用零点在频率‑波数平面上组成声波谐振器中弹性波的二维频散关系；本发明公开了一种快速且精确确定声波谐振器中弹性波二维频散关系的数值方法，从而确定弹性波在谐振器结构中传播时其频率和传播波数间的定量关系，在得到频散关系后，可以进一步确定声波谐振器的模态振型和谐振频率，从而决定声波谐振器实际工作时的模态和频率选择，为声波器件的结构设计和应用提供参考。

技术研发人员：赵梓楠,陈伟球,李念,韩佳鹏,沈旭栋
受保护的技术使用者：浣江实验室
技术研发日：
技术公布日：2024/10/21