一种基于传感器网络的分布式耦合张量流分解方法

本发明属于信号处理领域，尤其是涉及一种基于传感器网络的分布式耦合张量流分解方法。

背景技术：

1、张量将矩阵推广到了两个以上的维度，高阶张量及其分解普遍应用于信号处理、数据分析和机器学习等领域。在传感器网络(sn)中，不同传感器观测到的特征可能会出现重叠，可以用耦合张量模型表示测量的多维数据，从而捕获多维特征。由于大多数的张量分解算法都是针对批处理提出的，而针对数据流的研究相对较少，因此对耦合张量流分解的研究意义很大。

技术实现思路

1、针对上述问题，本发明提出一种基于传感器网络的分布式耦合张量流分解方法。

2、本发明采用的技术方案为：

3、一种基于传感器网络的分布式耦合张量流分解方法，包括以下步骤：

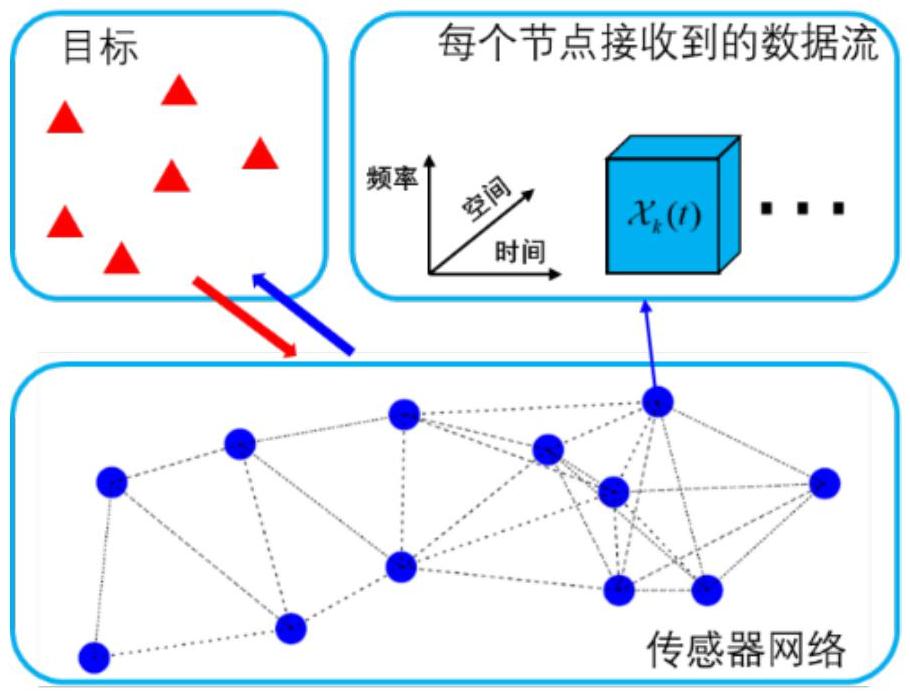
4、s1、对于如图1所示的分布式传感器网络，设定表示传感器节点构成的有向动态图，节点集为随时间变化的边集表示双向数据链路，将传感器节点k在t时刻的邻域记为并且表示节点k在t时刻的度；

5、s2、将时刻t在传感器节点k处接收到的张量切片建模为：

6、

7、其中，是在时刻t和节点k∈v处的n阶张量流，秩为r；是n阶的单位对角张量，满足当且仅当r1＝…＝rn时否则表示节点k第p个共享因子矩阵，p＝1,…,p；表示节点k的私有因子矩阵，iq是张量流中iq-1维张量的个数，q＝p+1,…,n；是节点k在t时刻的第n个因子矩阵；是张量测量噪声；

8、s3、仅考虑因子矩阵的随机游走，同时固定模n并假设当n′≠n且n′＝1,2,...,n时已知，建立耦合张量流分解的凸优化问题为：

9、

10、其中，是根据的时变因子矩阵；f(·)是因子矩阵的固有动态模型；是每个传感器节点处的过程噪声；是一般凸损失函数，ωk是权重；

11、s4、利用交替方向乘子法求解s3建立的凸优化问题，在frobenius范数的条件下，对增广拉格朗日函数中的三个参数进行初始化得到其中是对偶变量，n＝1,...,n，则在第j次迭代中共享因子矩阵的更新如下：

12、

13、其中，y(p),k(t)是任意节点k接收到的张量沿模-p的展开且z⊙表示khatri-rao乘积，表示转置，是第j-1次迭代得到的节点k的第p个共享因子矩阵，是第j-1次迭代得到的对偶变量，x是优化变量，j＝1,2,…，ρ是正则化因子；

14、第p个共享因子矩阵的更新方式如下：

15、

16、其中第j次迭代得到的对偶变量k是传感器网络中的节点数，p＝1,…,p；

17、如果当前迭代估计的共享因子矩阵与前一次迭代估计的结果近似，两者差距符合设定的收敛条件，此时迭代优化终止；

18、s5、在较松弛的条件下张量分解是唯一的，可使用交替最小二乘法估计每个传感器节点的因子矩阵。需要注意的是，如果张量分解不唯一，得到的因子矩阵并不具备可靠的研究意义。利用交替最小二乘法得到第j次迭代估计的因子矩阵为：

19、

20、式中：是节点k经过第j次迭代估计得到第p个共享因子矩阵，是节点k经过第j次迭代估计得到第q-p个私有因子矩阵，ir是秩为r的单位矩阵，

21、p＝1,…,p且q＝p+1,…,n；

22、s6、利用平均共识算法提高节点间共享因子矩阵的准确性，首先设定以及p＝1,…,p，再根据s5的因子矩阵进行cp分解，并且仅依靠每个节点接收到的张量切片得到节点k的估计因子矩阵然后在每个节点上对共享因子矩阵进行平均共识，其中wk,k(t)是节点k的当前自权重，wk,k′(t)是节点k赋予邻点k′的共识权重，具体为：

23、在平均共识迭代算法的初始阶段，设定节点k的第p个因子矩阵和其对偶变量为有：

24、

25、其中，与分别是节点k经过第l次共识迭代得到的第p个因子矩阵和对偶变量，与分别是邻点k′经过第l-1次共识迭代得到的第p个因子矩阵和对偶变量；

26、当完成l次迭代后，令p＝1,…,p有：

27、

28、其中，与分别是节点k经过第l次共识迭代得到的第p个因子矩阵和对偶变量，是节点k第p个估计的因子矩阵；

29、使用共识的结果作为t+1时刻的交替最小二乘算法的初始值，并重复p次迭代过程；

30、s7、迭代优化结束后，得到节点k的估计因子矩阵为

31、本发明的有益效果：本发明是一种关于完全分布式的耦合张量流分解方法。首先假设所有传感器的测量数据均可用，并且不能使用分布式方法处理，从而推导出耦合张量流分解算法；然后利用平均共识(ac)算法对相同特征进行融合，从而实现以完全分布式方法来进行张量流分解。本方法无需之前时间点的张量测量数据，计算复杂度不会随时间增大，因为当前时刻对每个维度估计的参数都会用于下一时刻的初始化。计算机仿真结果表明本发明使用完全分布式的方式，维持了每个节点的私有维度；仅通过传感器网络交换共享因子矩阵，保证了低的通信复杂度。

技术特征：

1.一种基于传感器网络的分布式耦合张量流分解方法，其特征在于，包括以下步骤：

技术总结
本发明属于信号处理领域，尤其是涉及一种基于传感器网络的分布式耦合张量流分解方法。本发明假设所有传感器的测量数据均可用，并且不能使用分布式方法处理，从而推导出耦合张量流分解算法；然后利用平均共识(AC)算法对相同特征进行融合，从而实现以完全分布式方法来进行张量流分解。本方法无需之前时间点的张量测量数据，计算复杂度不会随时间增大，因为当前时刻对每个维度估计的参数都会用于下一时刻的初始化。本方法使用完全分布式的方式，维持了每个节点的私有维度；仅通过传感器网络交换共享因子矩阵，保证了低的通信复杂度。

技术研发人员：张花国,付裕,刘传现,李亮亮
受保护的技术使用者：电子科技大学
技术研发日：
技术公布日：2024/11/11