一种基于正交多项式分解的量子态重构方法及系统与流程

本发明涉及量子信息，尤其涉及一种基于正交多项式分解的量子态重构方法及系统。

背景技术：

1、大气环流问题对于理解和应对地球环境、气候变化和人类活动的影响至关重要。研究大气环流主要包括研究大气的传输和扩散，这其中包含了许多非线性过程。为了模拟非线性波动，我们通常需要使用到如burgers之类的非线性偏微分方程来求解大气环流问题。

2、在数据量不断增长的背景下，计算效率成为求解非线性偏微分方程时需要考虑的关键因素。量子计算在解决非线性偏微分方程问题上，已经展示出计算效率上的潜力，现在已经被证明可以用于求解burgers方程。

3、在量子信息领域中，量子态是描述量子系统的状态，包含了系统的所有信息。由于量子计算的方法需要通过反复测量量子态来得到统计结果，这些统计结果反映了系统的求解结果。，所以加速量子态“重构”的过程就至关重要，这决定了量子计算的效率。量子态重构是是从测量数据中完全表达出被重构量子态的信息的过程。然而，对于大系统，传统的量子态重构方法需要指数级的测量资源，因此寻找有效的重构方法是研究方向的重点。以下介绍几种现有的有效的量子态重构方法。

4、弱测量技术只需要对每个量子比特执行一个强测量或弱测量，从而降低了测量复杂度。但弱测量的信号通常远小于噪声水平，意味着测量结果会出现很大的误差，并且需要高精度的仪器设备。

5、基于压缩感知理论的方法可以通过测量数据的稀疏性来重构量子态。这种方法可以通过少量测量来准确还原稀疏的量子态，提高重构效率，但对于非稀疏的量子态，效果可能比较差。

6、局域约化密度矩阵测量只测量局部信息，从而减少测量资源。但这要求解的全局量子态在局域约化密度矩阵信息下具有一定的唯一确定性属性（ud）。这类方法可以通过局部测量实现量子态重构，但在应用中需要考虑系统的特性。

7、因而，现有的量子态重构方法都需要对量子态的密度矩阵进行测量，复杂度很高，或是有极高的约束条件，造成重构的效率和效果均低。

技术实现思路

1、基于背景技术存在的技术问题，本发明提出一种基于正交多项式分解的量子态重构方法及系统，降低了重构的复杂度，从而提高了重构的效率和效果。

2、一种基于正交多项式分解的量子态重构方法，包括如下步骤：

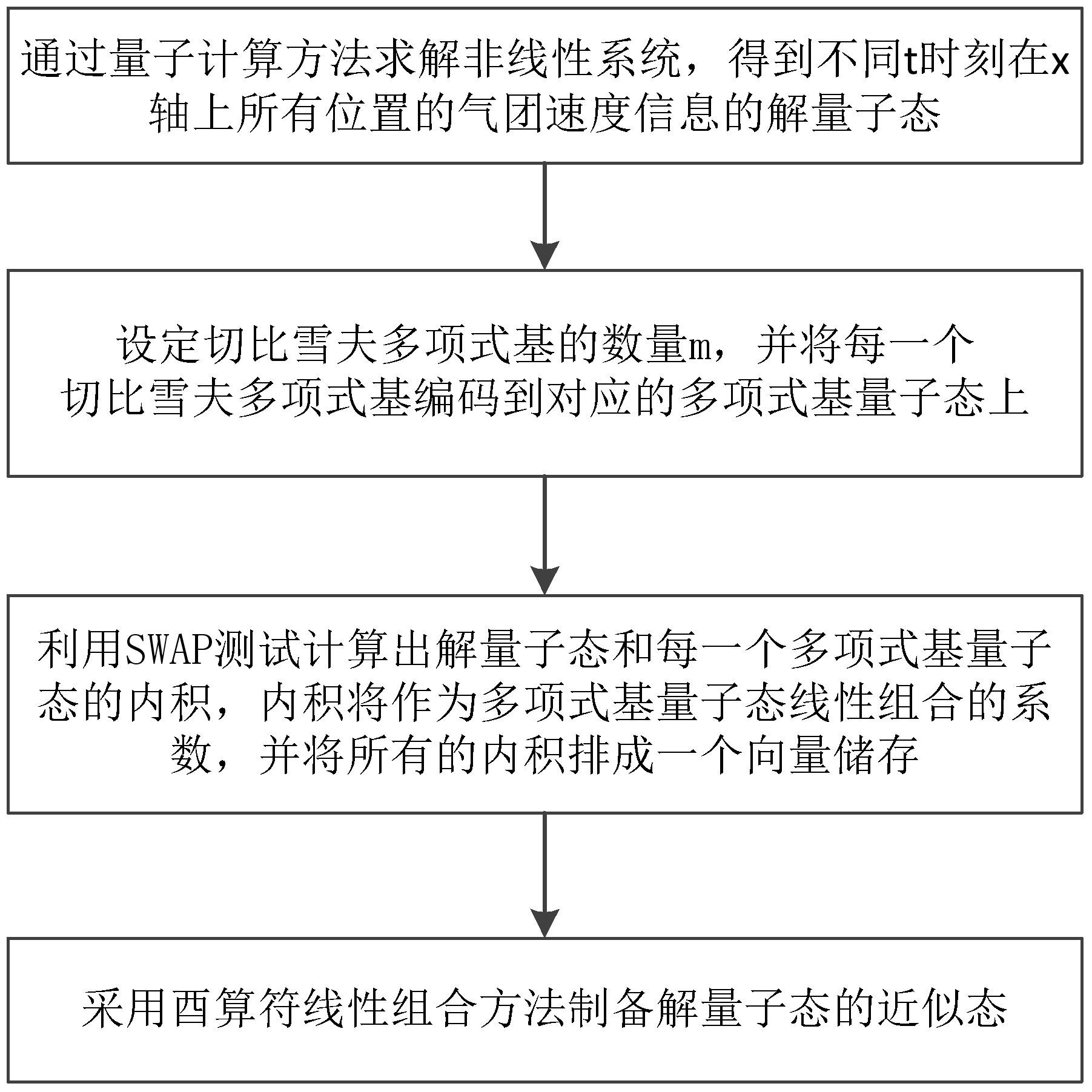
3、s1、通过量子计算方法求解非线性系统，得到不同时刻在轴上所有位置的气团速度信息的解量子态；

4、s2、设定切比雪夫多项式基的数量，并将每一个切比雪夫多项式基编码到对应的多项式基量子态上；

5、s3、利用swap测试计算出解量子态和每一个多项式基量子态的内积，内积将作为多项式基量子态线性组合的系数，并将所有的内积排成一个向量储存；

6、s4、采用酉算符线性组合方法制备解量子态的近似态；

7、s41、初始化个控制量子比特，并在初态上作用一个酉矩阵，所述酉矩阵为用于将初态转变为向量的振幅编码态形式，利用个控制量子比特代表的个控制量子态，分别控制在工作量子比特上执行，每个作用在工作比特上时，得到相应的多项式基量子态，其中表示第次操作，表示量子线路的张量积运算，；

8、s42、作用一个酉矩阵，并选择个控制量子比特中的所有量子比特位测到的结果，此时工作量子比特位上的量子态即为近似态，其中所述酉矩阵表示执行酉操作的逆操作。

9、进一步地，在步骤s2中，将每一个切比雪夫多项式基编码到对应的多项式基量子态上，具体为：

10、针对所有切比雪夫多项式基，在[-1,1]区间上等间隔的取个点，获取每个点对应的切比雪夫多项式基函数值，并将所有切比雪夫多项式基函数值按序排为向量，以生成多项式基向量，为解量子态所作用量子比特的数量，即所述步骤s41中的工作比特的数量为；

11、将每个多项式基向量通过量子态振幅编码到对应的多项式基量子态上，实现多项式基量子态的制备。

12、进一步地，在s3中，利用swap测试计算出解量子态和每一个多项式基量子态态的内积，具体为：

13、初始化一个辅助量子比特，并在所述辅助量子比特上作用一个hadamard门；

14、当辅助量子比特为时，应用步骤s2制备多项式基量子态的操作，当辅助量子比特为时，应用步骤s1制备解量子态的操作；

15、在辅助量子比特上再次应用hadamard门，并对辅助量子比特进行测量；

16、根据辅助量子比特的测量结果，计算出多项式基量子态和解量子态的内积。

17、一种基于正交多项式分解的量子态重构系统，包括第一计算模块、转化模块、第二计算模块和重构模块，重构模块包括第一作用单元和第二作用单元；

18、第一计算模块用于通过量子计算方法求解非线性系统，得到不同时刻在轴上所有位置的气团速度信息的解量子态；

19、转化模块用于设定切比雪夫多项式基的数量，并将每一个切比雪夫多项式基编码到对应的多项式基量子态上；

20、第二计算模块用于利用swap测试计算出解量子态和每一个多项式基量子态态的内积，内积将作为多项式基量子态线性组合的系数，并将所有的内积排成一个向量储存；

21、重构模块用于采用酉算符线性组合方法计算重构的近似态；

22、第一作用单元初始化个控制量子比特，并在初态上，作用一个酉矩阵，所述酉矩阵为用于将初态转变为向量的振幅编码态形式，利用个控制量子比特代表的个控制量子态，分别控制在工作量子比特上执行，每个作用在工作比特上时，得到相应的多项式基量子态，其中表示第次操作，表示量子线路的张量积运算，；

23、第二作用单元作用一个酉矩阵，并选择个控制量子比特中的所有量子比特位测到的结果，此时工作量子比特位上的量子态即为近似态，其中所述酉矩阵表示执行酉操作的逆操作。

24、进一步地，第二计算模块包括第一计算单元和第二计算单元；

25、第一计算单元用于初始化一个辅助量子比特，并在所述辅助量子比特上作用一个hadamard门，当辅助量子比特为时，应用步骤二制备多项式基量子态的操作，当辅助量子比特为时，应用步骤一制备解量子态的操作；

26、第二计算单元在辅助量子比特上再次应用hadamard门，并对辅助量子比特进行测量，根据辅助量子比特的测量结果，计算出多项式基量子态和解量子态的内积。

27、本发明提供的一种基于正交多项式分解的量子态重构方法及系统的优点在于：适用于任意量子态的重构，并且复杂度低至级别，对量子计算求解的非线性系统中的量子态进行高效便捷的重构后，加速了量子系统求解非线性问题时从解量子态中得到系统在经典上对应的实际结果的过程。

技术特征：

1.一种基于正交多项式分解的量子态重构方法，其特征在于，量子态重构方法包括如下步骤：

2.根据权利要求1所述的基于正交多项式分解的量子态重构方法，其特征在于，在步骤二中，将每一个切比雪夫多项式基编码到对应的多项式基量子态上，具体为：

3.根据权利要求1所述的基于正交多项式分解的量子态重构方法，其特征在于，在s3中，利用swap测试计算出解量子态和每一个多项式基量子态的内积，具体为：

4.一种基于正交多项式分解的量子态重构系统，其特征在于，包括第一计算模块、转化模块、第二计算模块和重构模块，重构模块包括第一作用单元和第二作用单元；

5.根据权利要求4所述的基于正交多项式分解的量子态重构系统，其特征在于，第二计算模块包括第一计算单元和第二计算单元；

技术总结
本发明公开了一种基于正交多项式分解的量子态重构方法及系统，涉及量子信息技术领域，通过量子计算方法求解非线性系统，得到不同时刻在轴上所有位置的气团速度信息的解量子态；设定切比雪夫多项式基的数量，并将所有个切比雪夫多项式基分别编码到对应的多项式基量子态上；利用SWAP测试计算出解量子态和每一个多项式基量子态的内积，内积将作为多项式基量子态线性组合的系数，并采用酉算符线性组合方法制备解量子态的近似态；该量子态重构方法降低了重构过程的复杂度，由于量子态重构是量子计算解决非线性系统分析必不可少的一步，因此该量子态重构方法对求解非线性系统分析问题实现了加速。

技术研发人员：方宇,薛程,陈昭昀
受保护的技术使用者：合肥综合性国家科学中心人工智能研究院（安徽省人工智能实验室）
技术研发日：
技术公布日：2024/9/17