基于LSTM算法的车-线-桥耦合振动加速计算方法

本发明属于车桥耦合计算加速领域，尤其涉及一种基于lstm算法的车-线-桥耦合振动加速计算方法。

背景技术：

1、随着中国高速铁路桥梁向结构复杂化，柔性化发展，同时铁路列车车速不断提升。列车过桥时，首先会引起桥梁的变形与振动，直接影响桥梁局部动力性能和使用寿命；另一方面，桥梁的振动同时也会影响列车过桥时的行车安全性与乘坐舒适性，甚至极端情况下会导致列车脱轨等严重事故。因此列车桥梁耦合动力计算的研究对于提高桥梁结构稳定性与耐用性以及列车行车安全性与舒适性具有深远的意义。

2、传统车-桥耦合计算方法主要依赖于有限元分析(fea)，这种方法在计算上非常密集且耗时，尤其是处理复杂或大规模结构时更是如此。这些常规技术在快速适应桥梁在不同载荷和环境影响下的变化条件方面常常存在挑战，计算效率低下。

3、现有的一种技术方案基于多系统耦合的结构动力学理论，针对公铁两用桥列车过桥时的桥梁车辆动力响应进行了计算，该方法理论明确，结果明晰。但是该方法涉及大型结构动力学矩阵数值积分方法求解，对计算机性能要求较高且相对耗时。

技术实现思路

1、针对现有技术中的上述不足，本发明提供的一种基于lstm算法的车-线-桥耦合振动加速计算方法解决了现有车桥耦合计算中计算耗时、效率低下的问题。

2、为了达到上述发明目的，本发明采用的技术方案为：一种基于lstm算法的车-线-桥耦合振动加速计算方法，包括以下步骤：

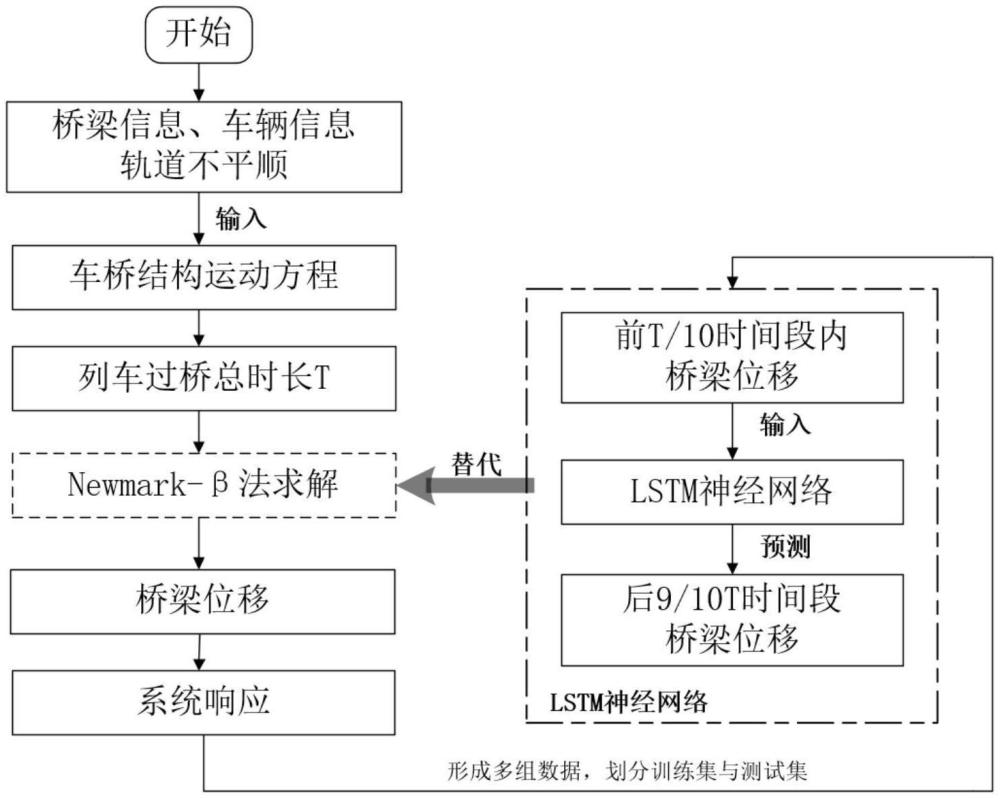
3、s1、基于车桥耦合理论，建立用于求解桥梁和列车动力响应时程的车桥耦合计算模型；

4、s2、获取若干组桥梁信息，利用车桥耦合计算模型，获取桥梁的动力响应，并建立桥梁响应初始响应与后续响应对应关系数据集，其中，后续响应为初始响应时刻后的响应；

5、s3、利用桥梁响应初始响应与后续响应对应关系数据集对lstm神经网络进行训练，得到训练完成的lstm网络；

6、s4、输入新的桥梁信息，利用训练完成的lstm网络由前序时间下车桥耦合计算模型计算的桥梁响应直接递归出后续桥梁响应，完成对车桥耦合计算的加速。

7、进一步地，所述步骤s1具体为：

8、s101、基于车桥耦合理论对桥梁建立有限元模型，并对列车建立多体动力学模型；

9、s102、根据有限元模型和多体动力学模型，将轨道不平顺作为激励，构建系统运动方程；

10、s103、通过数值积分方法在时域中对系统运动方程进行求解，得到桥梁和列车动力响应时程；

11、s104、基于步骤s101-s103构建车桥耦合计算模型。

12、进一步地，所述步骤s102中系统运动方程的表达式为：

13、

14、

15、fv-b＝kwi×db

16、dbi＝xbi+ri

17、其中，mv为列车子系统的质量矩阵；为列车子系统的加速度向量；cv为列车子系统的阻尼矩阵；为列车子系统的速度；kv为列车子系统的刚度矩阵；xv为列车子系统的位移；fv-b和fb-v均为列车与桥梁间相互作用力；mb为桥梁子系统的质量矩阵；为桥梁子系统的加速度向量；cb为桥梁子系统的阻尼矩阵；为桥梁子系统的速度；kb为桥梁子系统的刚度矩阵；xb为桥梁子系统的位移；kwi为列车每个轮对的刚度；db为每个车轮下桥梁空间实际位置；dbi为桥梁第i个节点的实际位置；xbi为桥梁子系统第i个节点的动态位移；ri为桥梁节点i位置处的不平顺值。

18、进一步地，所述步骤s103中数值积分方法的积分表达式为：

19、

20、其中，xn+1为第n+1个积分步的位移；δt为时间积分步长；α和β均为积分参数；为第n+1个积分步的加速度向量；为第n+1个积分步的速度。

21、进一步地，所述步骤s103具体为将系统运动方程代入数值积分方法的积分表达式求解桥梁和列车动力响应时程。

22、进一步地，所述步骤s2中桥梁的动力响应具体为桥梁主梁各节点的位移响应时程序列。

23、本发明的有益效果为：本发明利用车桥耦合作用中，桥梁初始阶段位移所包含的桥梁刚度、列车参数等信息，通过lstm神经网络提取桥梁位移时间序列中的特征，达到对后续长时间的桥梁位移进行智能预测的目的，从而实现对车桥耦合计算的加速，并且适应铁路桥梁多类型、多跨度的复杂情况。同时lstm神经网络作为rnn循环神经网络的一个优秀发展，保持了其对时间序列递归预测的能力且克服了rnn中可能出现的梯度消失或梯度爆炸问题。本发明克服了现有技术计算效率低、耗时长的缺点，利于后续智能交通系统的高频或实时操作数据的需求。

技术特征：

1.一种基于lstm算法的车-线-桥耦合振动加速计算方法，其特征在于，包括以下步骤：

2.根据权利要求1所述基于lstm算法的车-线-桥耦合振动加速计算方法，其特征在于，所述步骤s1具体为：

3.根据权利要求2所述基于lstm算法的车-线-桥耦合振动加速计算方法，其特征在于，所述步骤s102中系统运动方程的表达式为：

4.根据权利要求2所述基于lstm算法的车-线-桥耦合振动加速计算方法，其特征在于，所述步骤s103中数值积分方法的积分表达式为：

5.根据权利要求2所述基于lstm算法的车-线-桥耦合振动加速计算方法，其特征在于，所述步骤s103具体为将系统运动方程代入数值积分方法的积分表达式求解桥梁和列车动力响应时程。

6.根据权利要求1所述基于lstm算法的车-线-桥耦合振动加速计算方法，其特征在于，所述步骤s2中桥梁的动力响应具体为桥梁主梁各节点的位移响应时程序列。

技术总结
本发明公开了一种基于LSTM算法的车‑线‑桥耦合振动加速计算方法，属于车桥耦合计算加速领域，该方法包括基于车桥耦合理论，建立用于求解桥梁和列车动力响应时程的车桥耦合计算模型；获取若干组桥梁信息，利用车桥耦合计算模型，获取桥梁的动力响应，并建立桥梁响应初始响应与后续响应对应关系数据集；利用桥梁响应初始响应与后续响应对应关系数据集对LSTM神经网络进行训练，得到训练完成的LSTM网络；输入新的桥梁信息，利用训练完成的LSTM网络由前序时间下车桥耦合计算模型计算的桥梁响应直接递归出后续桥梁响应，完成对车桥耦合计算的加速。本发明解决了现有车桥耦合计算中计算耗时、效率低下的问题。

技术研发人员：李小珍,贺浩楠,王铭,王矗峰,郑禹豪,程益凡,骆仁舜
受保护的技术使用者：西南交通大学
技术研发日：
技术公布日：2024/12/23