基于分数阶时域统计矩的结构模态振型识别方法

本发明涉及模态识别相关领域，具体是基于分数阶时域统计矩的结构模态振型识别方法。

背景技术：

1、基本模态振型的识别，在结构动力学特性分析、结构振动控制、优化设计以及损伤检测等方面获得重要应用，因此，准确识别结构模态对于及早发现结构异常、避免重大事故发生具有至关重要的作用。

2、目前，基于传感器和采集系统进行结构模态参数的识别方法，已经成为结构健康监测一种高效和实用的动力特性检测方法，但是在存的方法中，并无通过分数阶时域统计矩进行识别，在对于结构模态参数的识别时，考虑环境噪音、计算效率以及测量误差等影响，距离实际应用还有一定距离，因此缺少一种精度以及抗噪性更佳的模态识别方法，并应用于实际工程的方法

技术实现思路

1、为解决上述技术问题，本发明的目的在于提供基于分数阶时域统计矩的结构模态振型识别方法。

2、基于此，本发明提出了基于分数阶时域统计矩的结构模态振型识别方法，该方法包括以下步骤：

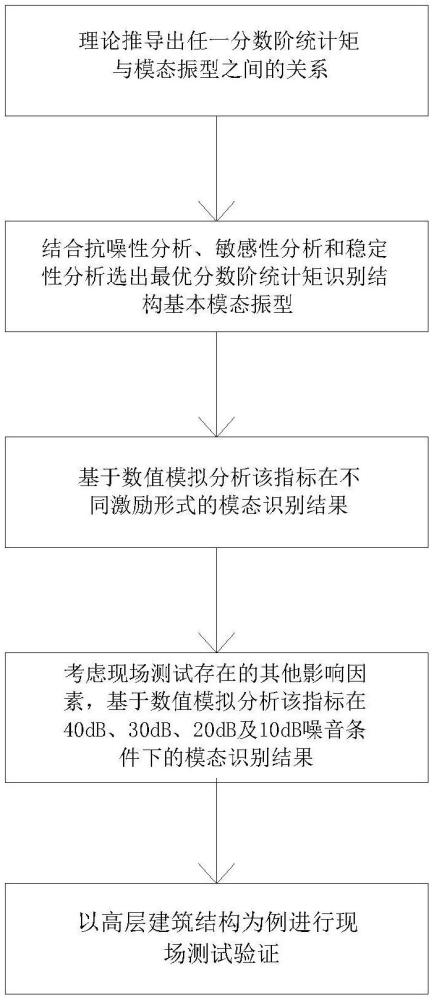
3、步骤s1：理论推导出任一分数阶统计矩与模态振型之间的关系；

4、s11：首先进行单自由度分数阶统计矩的分析，根据统计矩理论,对于线弹性结构，其结构响应的阶时域统计矩可表示为：

5、式中，表示阶时域统计矩；x和μ分别表示结构响应和响应的均值；p(x)表示结构响应的概率密度函数，通过方差和功率谱密度函数可推导出阶时域位移统计矩和加速度统计矩；

6、

7、gamma函数；m,k,ξ分别表示结构的质量、刚度和阻尼比；s0为激励功率谱密度函数值，当激励为理想白噪声时，s0为定值；

8、s12：接着根据多自由度分数阶统计矩进行分析，多自由度结构受到地面加速度激励的运动方程为：

9、式中，m,c,k分别表示结构质量矩阵、阻尼矩阵和刚度矩阵；分别表示结构响应加速度响应向量、速度响应向量和位移响应向量；p(t)为外部激励；i为单位列向量，通过假设结构为rayleigh阻尼，根据利用振型正交性对其进行解耦，从而求出结构振型反应运动方程，通过计算推导得出加速度统计矩与模态之间的类似关系，对于多自由度体系，阶分数位移统计矩和加速度统计矩均与振型有对应关系；

10、步骤s2：结合抗噪性分析、敏感性分析和稳定性分析选出最优分数阶统计矩识别结构基本模态振型；

11、s21：在现场测量时，周边环境噪音的干扰不可避免，噪音对刚度变化的影响只和噪音强度有关，以一个单自由度结构为模型，模拟不同分数阶统计矩的抗噪性，从而判断出噪音对识别结果的影响；

12、所述的单自由度结构为模型，其该结构质量为276kg，抗侧刚度为4.97*105n/m，阻尼比为0.05，荷载激励设置为均值等于零的高斯白噪音，持续时间为30s，采样频率为100hz；

13、s22：接着对其进行敏感性分析，从而判断出相同分数阶数的位移统计矩敏感性大于加速度统计矩；

14、s23：最后对分数阶统计矩的稳定性分析，选取随机产生的20组不同的高斯白噪音激励，获得不同的时程响应，求解不同分数阶统计矩的均值和标准差以及对应的变异系数；

15、步骤s3：基于数值模拟分析该指标在不同激励形式的模态识别结果；

16、s31：依托33层高层建筑结构作为分析模型，采用瑞丽阻尼和法求解给定激励下的动力响应；

17、所述的依托33层高层建筑结构作为分析模型，其中模型中梁柱的弹性模量均为7.751×109n/m2，各层层高为0.3m，跨度为0.6m，阻尼比为0.05，梁柱线密度分别为43.911kg/m和7.35kg/m；

18、s32：在现场测试中，首先，在结构同一竖直线上布置传感器获取加速度响应；然后采用带通滤波获取一阶频率对应的响应信号；其次计算出最优分数阶统计矩—最后根据理论推导公式求解模态振型；

19、步骤s4：考虑现场测试存在的其他影响因素，基于数值模拟分析该指标在40db、30db、20db及10db噪音条件下的模态识别结果；

20、s41：在高层结构响应上施加信噪比为40db、30db、20db和10db的噪音，根据识别流程将识别出的一阶振型与有限元模型的理论计算值进行对比，验证模态振型识别效果；

21、s42：为验证所提方法对于非平稳激励的适用性，分别采用el-centro波和kobe波作为激励，在40db、30db、20db和10db条件下分析所提方法的识别效果，同样采用1-mac值进行量化；

22、步骤s5：以高层建筑结构为例进行现场测试验证；

23、s51：以为重庆某高层住宅为试验对象进行试验，将数采仪及配套设备置于中间楼层，沿上下楼层位置质心处布置水平加速度传感器，将不同测点的加速度时程响应进行滤波，积分得到位移响应信号，然后计算

24、所述的重庆某高层住宅为试验对象，该高层建筑结构一共33层，总高度约为102m，地下5层，层高约为4.5m，地上28层，层高约为2.8m；

25、s52：最后根据计算出的进行分析，指标识别振型的方法在实际高层建筑结构中具有较好的适用性。

26、本发明具有如下优点：本发明通过改进在此提供基于分数阶时域统计矩的结构模态振型识别方法，具有如下改进：

27、以高层建筑结构为例，通过理论推导，数值模型分析，并结合实测响应数据进行对比，理论推导出任一分数阶统计矩与模态振型的关系，通过抗噪性分析、敏感性分析和稳定性分析选出了最优分数阶统计矩-基于指标，通过数值模拟说明环境噪音和不同激励对识别一阶模态振型结果的影响较小，并与随机子空间方法进行对比，说明所提方法的准确性和高效率，本方法具有良好的抗噪性，不仅适用于高层建筑结构，同样适用于桥梁及其它建筑结构类型。

技术特征：

1.基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，该方法包括以下步骤：

2.根据权利要求1所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，如上步骤s1中所述的理论推导出任一分数阶统计矩与模态振型之间的关系具体步骤为：

3.根据权利要求1所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，如上步骤s2中所述的理论推导出任一分数阶统计矩与模态振型之间的关系具体步骤为：

4.根据权利要求1所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，如上步骤s3中所述的理论推导出任一分数阶统计矩与模态振型之间的关系具体步骤为：

5.根据权利要求1所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，如上步骤s4中所述的理论推导出任一分数阶统计矩与模态振型之间的关系具体步骤为：

6.根据权利要求1所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，如上步骤s5中所述的理论推导出任一分数阶统计矩与模态振型之间的关系具体步骤为：

7.根据权利要求2所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，所述的阶时域位移统计矩和加速度统计矩为以下公式计算：

8.根据权利要求3所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，所述的单自由度结构为模型，其该结构质量为276kg，抗侧刚度为4.97*105n/m，阻尼比为0.05，荷载激励设置为均值等于零的高斯白噪音，持续时间为30s，采样频率为100hz。

9.根据权利要求4所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，所述的依托33层高层建筑结构作为分析模型，其中模型中梁柱的弹性模量均为7.751×109n/m2，各层层高为0.3m，跨度为0.6m，阻尼比为0.05，梁柱线密度分别为43.911kg/m和7.35kg/m。

10.根据权利要求6所述的基于分数阶时域统计矩的结构模态振型识别方法，其特征在于，所述的重庆某高层住宅为试验对象，该高层建筑结构一共33层，总高度约为102m。地下5层，层高约为4.5m，地上28层，层高约为2.8m。

技术总结
本发明提供了基于分数阶时域统计矩的结构模态振型识别方法，包括，本发明提供了基于分数阶时域统计矩的结构模态振型识别方法，以高层建筑结构为例，通过理论推导，数值模型分析，并结合实测响应数据进行对比，理论推导出任一分数阶统计矩与模态振型的关系，通过抗噪性分析、敏感性分析和稳定性分析选出了最优分数阶统计矩‑基于指标，通过数值模拟说明环境噪音和不同激励对识别一阶模态振型结果的影响较小，并与随机子空间方法进行对比，说明所提方法的准确性和高效率，本方法具有良好的抗噪性，不仅适用于高层建筑结构，同样适用于桥梁及其它建筑结构类型。

技术研发人员：阳洋,王者伟,张旭,范元青
受保护的技术使用者：重庆大学
技术研发日：
技术公布日：2025/2/5