一种基于辛几何差分谱的信号降噪方法

本发明属于设备状态监测与诊断，具体涉及一种基于辛几何差分谱的信号降噪方法。

背景技术：

1、时频分析作为一种能同时反映信号频域与时域信息的信号分析技术，其常被用于各领域信号分析中。常用的时频分析方法包括小波变换(wavelettransform，简称wt)、经验模态分解(empirical mode decomposition，简称emd)、集合经验模态分解(ensembleempirical mode decomposition，简称eemd)、奇异谱分析(singular spectrum analysis，ssa)等。wt的多尺度特性使得不同信号可以选择不同的小波基函数和尺度，但wt是一种可调窗口的fourier变换，难以有效解决模态混叠等问题。emd在处理非平稳信号上时能把一个多分量复杂信号自适应地化为成多个模态函数的和，但在包络插值问题上存在模态混叠、欠包络及噪声鲁棒性差等缺陷。eemd在抑制emd的模态混叠问题上起到了一定的作用，但其无法完全中和添加的白噪声。ssa具有较强的噪声鲁棒性，但其依赖先验经验选择窗函数大小，无法保障其分解效果，尤其是在强背景噪声环境下。虽然上述方法在故障诊断中都具有良好的分解效果，但是在分析多模态耦合信号时，仍存在一定的局限性，如难以保护信号结构化信息、强噪声下分解不理想等。

2、近年来，相关学者基于辛几何理论，提出了多种辛几何模态分析方法，可以实现噪声剔除的同时完成信号结构化信息的保护。但辛几何谱分析(symplectic geometryspectralanalysis，简称sgsa)和辛几何模态分解(symplectic geometrymodedecomposition，简称sgmd)都存在缺陷。sgsa将其应用于时间序列分析，但该方法依赖经验选择嵌入维数，且没有给出终止准则；sgmd采用功率谱密度(power spectral density，简称psd)获取参数信息，尽管其能自适应地确定嵌入维数，但sgmd方法的特征值个数选择具有主观性，通常，前k个(k<r)个显著特征值包含真实信号的重要属性，而噪声信号则包含在剩余的(r-k)个特征值中。过高的svd阶数选择会导致滤波信号中包含噪声信息，从而阻碍所期望的去噪效果。相反，当所选的奇异阶数过低时，它可能会无意中过滤掉有价值的分量作为噪声。

3、针对现有时频分析方法存在的不足，发明人期望提供一种基于辛几何差分谱的信号降噪方法。

技术实现思路

1、本发明的目的在于克服传统技术中存在的上述问题，提供一种基于辛几何差分谱的信号降噪方法。本发明提供的方法能够实现对特征值个数的有效选取。并且，通过fft和一阶滞后差处理的应用，得到了辛几何差分谱。最后为差异建立了一个预先确定的阈值范围(由经验确定)，在辛几何差分谱中，超过该阈值的第一个差值之前的奇异值被保留，而其余的奇异值被无效。得到所需奇异值后，再由svd的逆求解矩阵,再代替协方差矩阵进行去噪分解，再从包络谱图中进行诊断。本发明所提供的方法，能够有效地提取包含丰富故障信息的分量，并且诊断效果较好。

2、为实现上述技术目的，达到上述技术效果，本发明是通过以下技术方案实现：

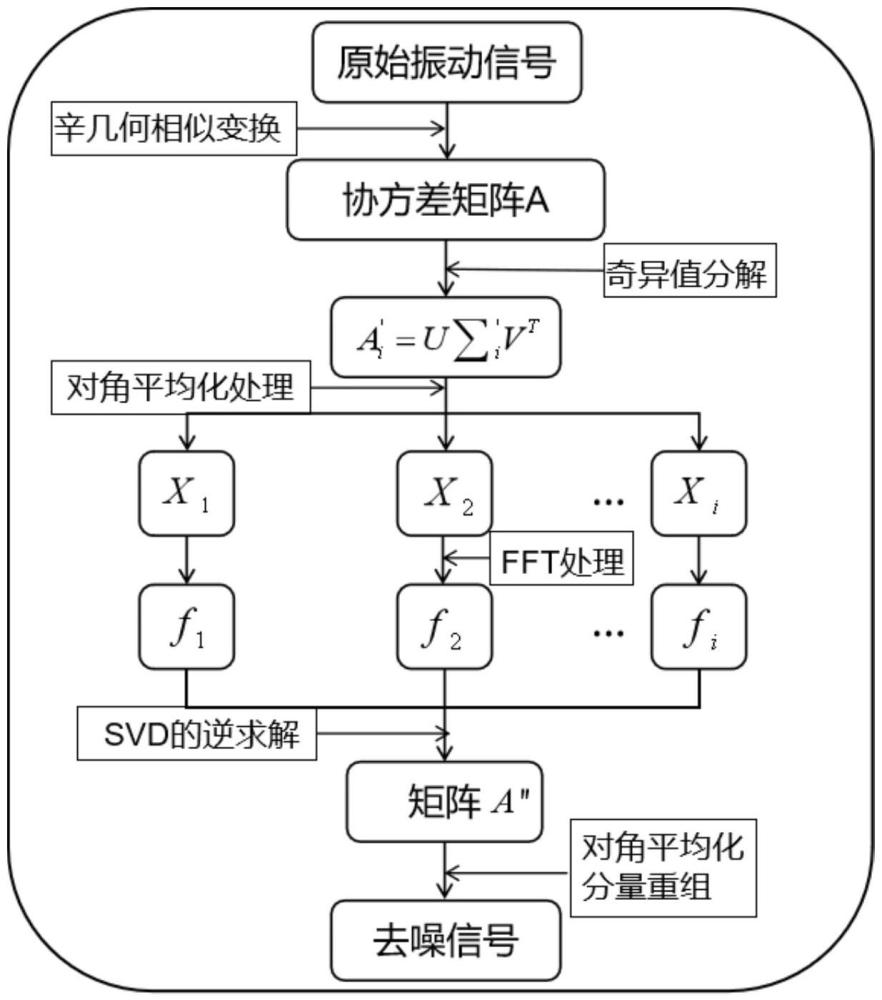
3、本发明提供一种基于辛几何差分谱的信号降噪方法，包括如下步骤：

4、s1、采集待诊断的原始振动信号；

5、s2、利用辛几何相似变换方法对原始振动信号进行分解；

6、s3、重组协方差矩阵，将快速傅里叶变换(fft)应用于该矩阵每个奇异值分量；

7、s4、选取最大振幅的频率值作为差分谱法中的指标特征；

8、s5、通过一阶滞后差处理，得到辛几何差分谱，设置阈值，选取所需奇异值，重组得到最终矩阵；

9、s6、将最终矩阵带回步骤s2中，得到去噪信号；

10、s7、对去噪信号进行包络谱分析；

11、s8、根据包络谱图识别状态特征。

12、进一步地，步骤s3中，对重组协方差矩阵并对其每个奇异值分量进行fft操作：

13、通过步骤s2辛几何相似变换得到协方差矩阵a后，对矩阵a进行svd分解，得到一系列奇异值按降序排列:

14、a＝u∑vt (1)

15、其中，正交矩阵u和v分别为a矩阵的左右奇异矩阵，∑为以下形式的奇异值矩阵：

16、

17、其中，δ＝diag(λ1,λ2,…,λr)，λ1≥λ2≥…≥λr≥0，λr为a矩阵的奇异值，r为该矩阵的秩，0为零矩阵；。

18、进一步地，在每次迭代δ中，只有一个λi被保留，而其余的奇异值被设置为零。

19、进一步地，迭代过程生成奇异值向量δ'i＝diag(0,…,λi,…,0)，以及奇异值矩阵和重组a矩阵，用以下形式表示：

20、

21、a′i＝uσ'ivt  (4)

22、将δ'i中的每个奇异值λi转换为一个具有奇异值的矩阵，然后使用奇异值分解对该矩阵进行倒置，得到变换矩阵a′i。

23、进一步地，将a′i矩阵进行对角平均化处理，得到与原始信号x对应的分量信号xi，将fft应用于每个xi分量信号。

24、进一步地，步骤s5中，构建辛几何差分谱选取最终矩阵的分步骤为：

25、1)识别各分量信号fft的频率值，选取各分量最大振幅的频率值，并将这些频率值根据原始信号的奇异值按降序排列；

26、2)通过一阶滞后差处理的应用，得到辛几何差分谱；

27、3)为了适应特定的情况，为差异建立一个预先确定的阈值。

28、进一步地，在辛几何差分谱中，超过该阈值的第一个差值之前的奇异值被保留，而其余的奇异值被无效。

29、进一步地，得到所需奇异值后，再由svd的逆求解重构矩阵a”。

30、本发明的有益效果是：

31、基于辛几何差分谱(sgds)的信号降噪技术摒弃sgmd直接采用奇异值分解选取特征值的降噪方式，本发明设计出一种选择奇异值去噪有效阶数的优化方法，该方法包括将振动信号的每个奇异值重构为一维信号，在频域内进行分析，并以振幅最高的频率值作为指标来表征每个奇异值分量。本发明通过选择第一个显著变化的频率值对应的奇异值阶作为算法的有效阶，使去噪算法的有效性最大化，实现对状态特征的有效提取，可以有效地得到特征频率及其倍频，对振动信号进行准确的诊断。

32、当然，实施本发明的任一产品并不一定需要同时达到以上的所有优点。

技术特征：

1.一种基于辛几何差分谱的信号降噪方法，其特征在于，包括如下步骤：

2.根据权利要求1所述的基于辛几何差分谱的信号降噪方法，其特征在于，步骤s3中，对重组协方差矩阵并对其每个奇异值分量进行fft操作为：

3.根据权利要求2所述的基于辛几何差分谱的信号降噪方法，其特征在于，在每次迭代δ中，只有一个λi被保留，而其余的奇异值被设置为零。

4.根据权利要求3所述的基于辛几何差分谱的信号降噪方法，其特征在于，迭代过程生成奇异值向量δ'i＝diag(0,…,λi,…,0)，以及奇异值矩阵和重组a矩阵，用以下形式表示：

5.根据权利要求4所述的基于辛几何差分谱的信号降噪方法，其特征在于，将a’i矩阵进行对角平均化处理，得到与原始信号x对应的分量信号xi，将fft应用于每个xi分量信号。

6.根据权利要求5所述的基于辛几何差分谱的信号降噪方法，其特征在于，步骤s5中，构建辛几何差分谱选取最终矩阵的分步骤为：

7.根据权利要求6所述的基于辛几何差分谱的信号降噪方法，其特征在于，在辛几何差分谱中，超过该阈值的第一个差值之前的奇异值被保留，而其余的奇异值被无效。

8.根据权利要求7所述的基于辛几何差分谱的信号降噪方法，其特征在于，得到所需奇异值后，再由svd的逆求解重构矩阵a”。

技术总结
本发明属于设备状态监测与诊断技术领域，具体涉及一种基于辛几何差分谱的信号降噪方法。本发明方法的步骤如下：采集待诊断的原始振动信号；利用辛几何相似变换方法对原始振动信号进行分解；重组协方差矩阵，将快速傅里叶变换(FFT)应用于该矩阵每个奇异值分量；选取最大振幅的频率值作为差分谱法中的指标特征；通过一阶滞后差处理，得到辛几何差分谱，设置阈值，选取所需奇异值，重组得到最终矩阵；将最终矩阵带回前述步骤中，得到去噪信号；本发明提供的信号降噪方法通过包络谱进行分析，能够根据包络谱图识别状态特征，且有效地得到特征频率及其倍频，诊断效果较好。

技术研发人员：潘海洋,许大洋,郑近德,童靳于,程健
受保护的技术使用者：安徽工业大学
技术研发日：
技术公布日：2025/2/13