一种LDPC码的校验矩阵的构造方法和装置与流程

本发明涉及无线通信领域，具体而言，本发明涉及ldpc码的校验矩阵的构造方法。

背景技术：

0、技术背景

1、shannon在著名的“通信的数学理论”中，阐明了在有噪声信道中实现可靠传输的途径是编码。他提出了有噪声信道中信息可传输的最大速率，即信道容量；同时也推导出了信息可无错误传输所需的最小信噪比值，被称为shannon极限。虽然shannon的信道编码理论给出了最佳编码的极限性能，但并没有给出具体的编码方案。以此为基础，人们一直致力于寻找性能上接近shannon极限的编码方案。

2、低密度奇偶校验(ldpc)码是一类能够逼近shannon限的性能优秀的信道纠错编码方案。ldpc码是一类特殊的线性奇偶校验分组码，其奇偶校验矩阵是“稀疏”的：只有非常小数目的非0矩阵元素(对于二进制码来说，非0元素即为元素1)，其它元素都为0。1960年，罗伯特·加拉格(robert gallager)在其博士论文中首次提出了ldpc码的概念，并提出了两种迭代译码算法，因此ldpc码又被称为gallager码。gallager从理论上指出，利用迭代译码算法(或消息传递算法)，ldpc码能够以较低的复杂度逼近信道容量。

3、ldpc码早期被忽视的原因也许是由于当时的计算机软硬件水平低下，人们无法从计算机仿真结果中得知ldpc码的优异性能；另外一种可能的原因是ldpc码需要较大的存储空间，这在当时是无法承受的；并且当时其它码类如里德—所罗门(reed-solomon)码和汉明(harming)码等是可用的，也就是说暂时存在可用的信道编码方案，人们就没有刻意地去研究ldpc码。

4、目前，ldpc码正被越来越多的应用于各种通信系统中。卫星广播系统通过卫星和地面基站实现天地一体的大面积广播覆盖，传送多路音视频广播业务，用户可以用终端实现移动接收。由于卫星信号功率受限，同步卫星轨道在36000公里高空，下行信号的路径损耗严重，导致接收终端的链路余量很小。因此，需要设计性能优秀的ldpc码。此外，实际的通信系统设计还需要实现低复杂度的编、译码过程。采用计算机搜索的方法获得性能优秀的ldpc码需要大量的算力，且校验矩阵存储和编码需要大量的存储和处理单元。

5、因此，有必要提出相应的技术方案，既可以构造多种码率的性能优秀的ldpc码，又能解决校验矩阵的存储及低复杂度快速编码的问题。

技术实现思路

1、本发明的目的旨在至少解決上述技术缺陷之一，特别是通过本发明提出的ldpc码的校验矩阵构造方法，构造出多种码率的性能优秀的ldpc码，解決校验矩阵的存储及低复杂度快速编码的问题。

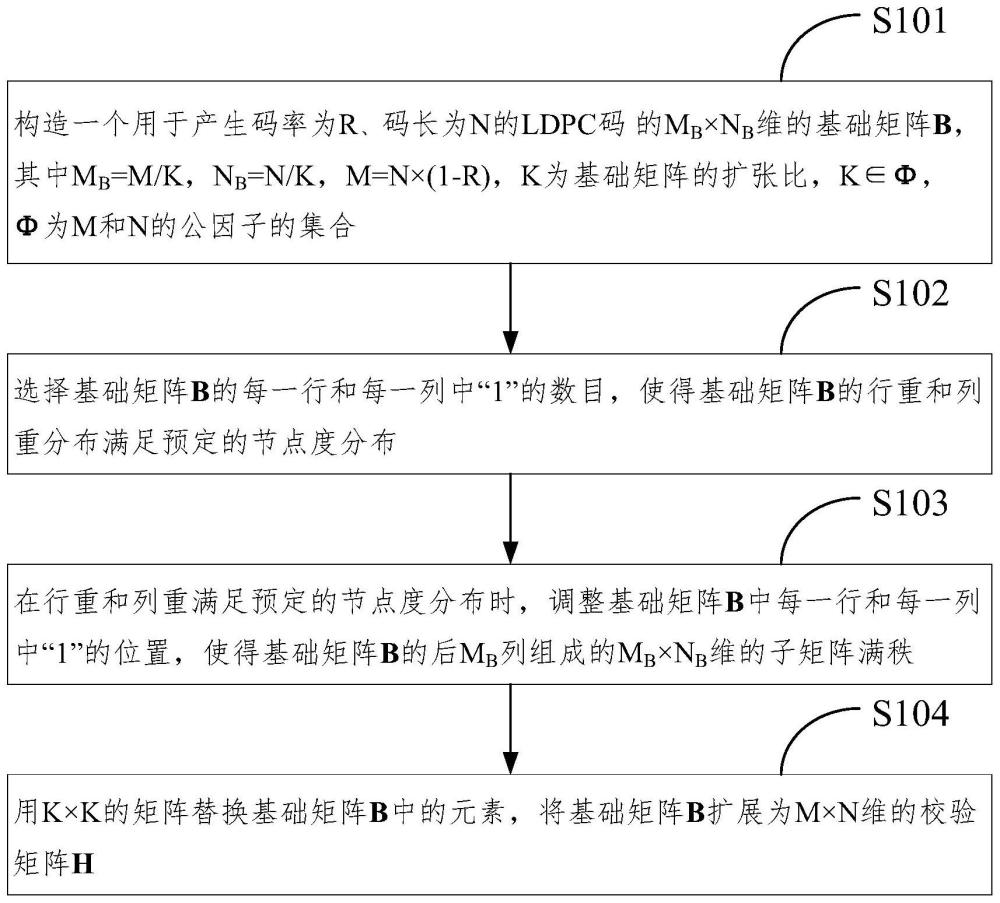
2、本发明的实施例的第一方面提出了一种ldpc码的校验矩阵的构造方法，所述方法包括：构造一个用于产生码率为r、码长为n的ldpc码的mb×nb维的基础矩阵b，其中mb＝m/k，nb＝n/k，m＝n×(1-r)，k为基础矩阵的扩张比，k∈φ,φ为m和n的公因子的集合；选择基础矩阵b的每一行和每一列中“1”的数目，使得基础矩阵b的行重和列重分布满足预定的节点度分布；在行重和列重满足预定的节点度分布时，调整基础矩阵b中每一行和每一列中“1”的位置，使得基础矩阵b的后mb列组成的mb×mb维的子矩阵满秩；用k×k的矩阵替换基础矩阵b中的元素，将基础矩阵b扩展为m×n维的校验矩阵h；所述用k×k的矩阵替换基础矩阵b中的元素，包括：将所述基础矩阵b中的“-1”用k×k维的全“0”矩阵z替换，将所述基础矩阵b中的非“-1”用k×k维的循环置换矩阵p替换，其中，循环置换矩阵p中“1”的行号i和列号j满足j＝(i+l)mod k，l为循环置换矩阵的偏移量，mod表示取模运算。

3、本发明的实施例的第二方面提出了一种ldpc码的校验矩阵的构造装置。所述ldpc码的校验矩阵的构造装置包括处理器和存储器：所述存储器中存储有计算机程序，所述计算机程序被所述处理器执行时实现如本发明的第一方面的任一项实施例所述的ldpc码的校验矩阵的构造方法的步骤。

4、本发明的实施例提出的ldpc码的校验矩阵的构造方案，通过为基础矩阵合适的选择合适的行重和列重，便于构造出合适码率的性能优秀的ldpc码。此外，本发明的实施例提出的技术方案可以解決校验矩阵的存储及低复杂度快速编码的问题。本发明的实施例提出的ldpc码的校验矩阵的构造方案，可以支持对生成的ldpc码的前1-1008比特信息进行任意打孔处理而不至于损失太大性能。

5、本发明附加的方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。

技术特征：

1.一种ldpc码的校验矩阵的构造方法，其特征在于，包括：

2.根据权利要求1所述的构造方法，其特征在于，在所述码长n为61488，所述码率r为20/61，所述扩展比k为504的情况下，

3.根据权利要求1所述的构造方法，其特征在于，在所述码率r为30/61，所述码长n为61488，所述扩展比k为504的情况下，

4.根据权利要求1所述的构造方法，其特征在于，在所述码率r为40/61，所述码长n为61488，所述扩展比k为504的情况下，

5.根据权利要求1所述的构造方法，其特征在于，在所述码率r为45/61，所述码长n为61488，所述扩展比k为504的情况下，

6.根据权利要求1所述的构造方法，其特征在于，在所述码率r为24/61，所述码长n为61488，所述扩展比k为504的情况下，

7.根据权利要求1所述的构造方法，其特征在于，在所述码率r为36/61，所述码长n为61488，所述扩展比k为504的情况下，

8.根据权利要求1所述的构造方法，其特征在于，在所述码率r为48/61，所述码长n为61488，所述扩展比k为504的情况下，

9.根据权利要求1所述的构造方法，其特征在于，在所述码率r为50/61，所述码长n为61488，所述扩展比k为504的情况下，

10.根据权利要求1所述的构造方法，其特征在于，在所述码率r为54/61，所述码长n为61488，所述扩展比k为504的情况下，

11.根据权利要求1所述的构造方法，其特征在于，在所述码率r为52/61，所述码长n为61488，所述扩展比k为504的情况下，

12.根据权利要求2所述的构造方法，其特征在于，所述基础矩阵b为：

13.根据权利要求3所述的构造方法，其特征在于，所述基础矩阵b为：

14.根据权利要求4所述的构造方法，其特征在于，所述基础矩阵b为：

15.根据权利要求5所述的构造方法，其特征在于，所述基础矩阵b为：

16.根据权利要求6所述的构造方法，其特征在于，所述基础矩阵b为：

17.根据权利要求7所述的构造方法，其特征在于，所述基础矩阵b为：

18.根据权利要求8所述的构造方法，其特征在于，所述基础矩阵b为：

19.根据权利要求9所述的构造方法，其特征在于，所述基础矩阵b为：

20.根据权利要求10所述的构造方法，其特征在于，所述基础矩阵b为：

21.根据权利要求11所述的构造方法，其特征在于，所述基础矩阵b为：

22.一种ldpc码的校验矩阵的构造装置，其特征在于，包括处理器和存储器：所述存储器中存储有计算机程序，所述计算机程序被所述处理器执行时实现如权利要求1-21任一项所述的ldpc码的校验矩阵的构造方法的步骤。

技术总结
本发明公开了一种LDPC码的校验矩阵的构造方法和装置。所述方法包括：构造一个用于产生码率为R、码长为N的LDPC码的M<subgt;B</subgt;×N<subgt;B</subgt;维的基础矩阵B，其中M<subgt;B</subgt;＝M/K，N<subgt;B</subgt;＝N/K，M＝N×(1‑R)，K为基础矩阵的扩张比，K∈Φ，Φ为M和N的公因子的集合；选择基础矩阵B的每一行和每一列中“1”的数目，使得基础矩阵B的行重和列重分布满足预定的节点度分布；调整基础矩阵B中每一行和每一列中“1”的位置，使得基础矩阵B的后M<subgt;B</subgt;列组成的M<subgt;B</subgt;×M<subgt;B</subgt;维的子矩阵满秩；用K×K的矩阵替换基础矩阵B中的元素，将基础矩阵B扩展为M×N维的校验矩阵H。

技术研发人员：盛志凡,胡军,肖婧婷,付瑞,张定京,夏治平,常琳
受保护的技术使用者：国家广播电视总局广播电视科学研究院
技术研发日：
技术公布日：2024/5/6