一种基于消息传递的多任务聚类稀疏重构方法

本发明属于信息与通信，尤其涉及一种基于消息传递的多任务聚类稀疏重构方法。

背景技术：

1、智慧物联网、超宽带通信、语义通信及人工智能等新型技术产业背景下的大数据呈爆炸式增长，海量数据为其分析和处理带来了前所未有的挑战。事实上，由于数据本身信息量的增长显著慢于数据维度的增长，高维海量数据之间往往存在冗余，使得其关键信息通常位于潜在的低维结构模式中。稀疏结构便是这些数据最为重要的低维结构特点，它为数据表达与分析、揭示事物内在本质属性提供了契机。基于先验稀疏结构，压缩感知理论应运而生，其是指当原信号或其在某个变换域内的表示系数充分稀疏时，则能够以远低于原信号维度的测量样本重建其高维信号。压缩感知为稀疏信号的亚奈奎斯特采集提供了理论基础，也使得信号处理产生了新思路和方法。在很多实际应用中(包括但不限于雷达探测、声呐定位、图像处理、无线通信等),感兴趣的目标相对应用背景而言可视为稀疏的。在压缩感知中，最为重要的任务为从少量欠定测量中对未知稀疏信号进行重构，高效且鲁棒的稀疏重构方法是实现其应用的先决条件。

2、传统稀疏重构方法包括贪婪算法(如文献《signal recovery from randommeasurements via orthogonal matching pursuit》中的omp算法)和基于凸优化的l1范数重构方法。根据合适的先验信息，贝叶斯稀疏重构方法得到了广泛关注和研究。文献《sparse bayesian learning and the relevance vector machine》基于分层的稀疏先验模型，率先提出了基于贝叶斯学习的稀疏重构方法，但该方法涉及矩阵求逆，当感知矩阵维度较大时，具有较高的计算复杂度，不利于实时应用。针对聚类稀疏重构问题，即稀疏信号的非零稀疏支集呈现一种未知的块状稀疏结构时，文献《generalized approximatemessage passing for estimation with random linear mixing》一般性稀疏先验，提出了一种基于消息传递的稀疏重构算法，具有较低的计算复杂度。然而，前述方法所探讨的问题为单任务稀疏重构问题，并不能直接应用于本发明所探讨的多任务块稀疏重构问题。多任务块稀疏重构问题的一个最为重要的特征为不同子任务下的稀疏信号具有相同的稀疏支集。通过合适的共同稀疏支集建模及合理利用，可以有效的提升稀疏信号的重构精确度，故同时兼具低计算复杂度及高精度的重构算法具有重要的研究价值。

技术实现思路

1、本发明的主要内容是提出一种基于贝叶斯消息传递的多任务聚类稀疏重构方法。本发明方法利用了不同任务间稀疏信号存在的联合聚类稀疏结构特征，使得在较少观测样本条件下，获得较好的稀疏重构性能。具体来说，通过马尔可夫spike and slab先验来描述聚类稀疏信号的稀疏结构特征，引入广义近似消息传递算法来迭代近似每个未知变量的后验均值，并采用期望-最大化方法对未知参数进行迭代更新。与传统的单任务贝叶斯压缩感知算法相比，在获取的观测样本较少的情况下，本发明方法有着显著的性能提升。

2、本发明采用的技术方案包括以下步骤：

3、s1、建立多任务块稀疏重构问题的数学模型，可表示为

4、yk＝akxk+wk，k＝1，...，k

5、其中，表示第k个任务中的测量向量，为块稀疏信号({xk}具有联合块稀疏结构)，wk为未知的零均值高斯噪声向量，(m《n)为第k个任务模型的感知矩阵或字典。

6、s2、对{xk}的块状稀疏结构进行建模。本发明使用马尔可夫spike and slabprior先验来描述这种聚类稀疏性，对任意k：

7、

8、由于为马尔可夫链，故稀疏支集可表示为：

9、

10、其中，为转移概率且具有如下伯努利条件概率分布：

11、

12、其中，和若p10越小，则sn-1取0值时sn取1值的概率越小，说明两个相邻的非零集群之间的平均距离越大。若p0i越小，则sn-1取1值时sn取0值的概率越小，说明非零集群平均大小越大。通过从p(xkn|sn)中计算xkn的边缘分布可得：

13、

14、其中，λ＝p10/(p01+p10)代表xk的稀疏度，即xkn为伯努利高斯分布。因此将初始p(s1)设为：

15、p(s1)＝λs1+(1-λ)(1-s1).

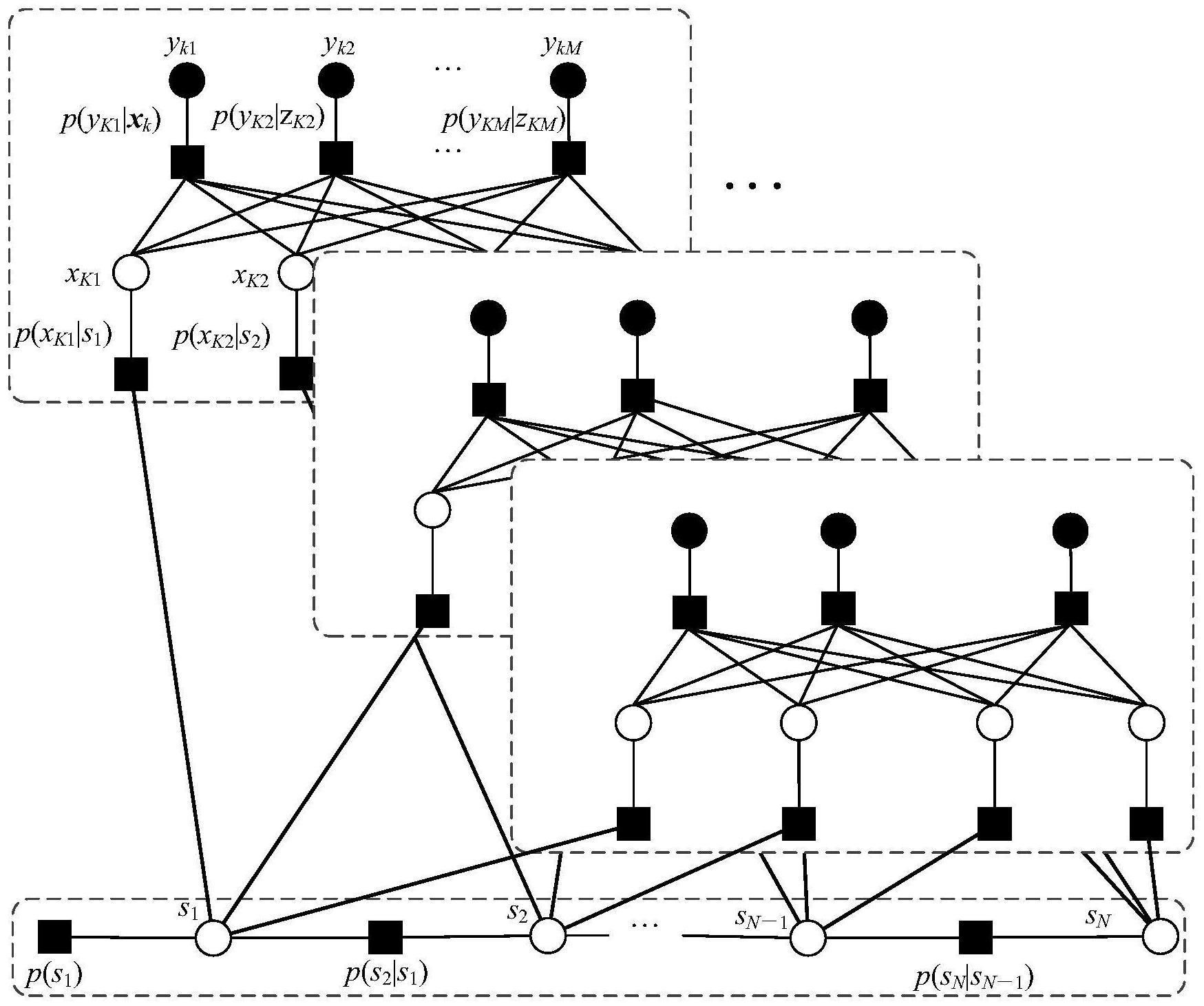
16、s3、因子图模型表示

17、由贝叶斯公式可推出对和s＝{s1，s2，...，sn}的联合概率分布为：

18、p(y，x，s)＝p(y|x，s)p(x|s)p(s)

19、在s已知时，对p(yk|xk)p(xk|s)是条件独立的，于是有

20、

21、由马尔可夫spike and slab prior先验的性质可得知，对p(xkn|sn)是相互独立的，可得(y，x，s)的联合概率分布为：

22、

23、在xk已知时，对p(ykm|xk)是相互独立的，于是有

24、

25、其中，zkm为zk中的第m个元素。p(ykm|zkm)为服从以zkm为均值，以σ2为方差的高斯分布，即

26、

27、由于x1，x2，...，xk有着联合的聚类稀疏结构，所以他们的稀疏性可用同一个马尔可夫spike and slab prior先验分布来表述，结合式(*1)中展示的随机变量之间的依赖关系建立因子图模型。根据因子图模型，然后可基于文献《generalized approximatemessage passing for estimation with random linear mixing》的消息传递方法得到因子图模型中各个变量之间的消息传递及均值计算方法。

28、s4、通过消息传递得到各个变量的边缘后验均值估计器，然后根据《patternrecognition and machine learning》中的期望最大化方法计算未知参数(噪声方差等)的迭代更新。步骤3和3交替迭代直至收敛。

29、本发明的有益效果是：通过马尔可夫spike and slab先验来描述聚类稀疏信号的稀疏结构特征，引入广义近似消息传递算法来迭代近似每个未知变量的后验均值，并采用期望-最大化方法对未知参数进行迭代更新。与传统的单任务贝叶斯压缩感知算法相比，在获取的观测样本较少的情况下，本发明方法有着显著的性能提升。

技术特征：

1.一种基于消息传递的多任务聚类稀疏重构方法，其特征在于，包括以下步骤：

技术总结
本发明提出了一种基于消息传递的多任务聚类稀疏重构方法。本发明方法利用了不同任务间稀疏信号存在的联合聚类稀疏结构特征，使得在较少观测样本条件下，获得较好的稀疏重构性能。具体来说，通过马尔可夫Spike and Slab先验来描述聚类稀疏信号的稀疏结构特征，引入广义近似消息传递算法来迭代近似每个未知变量的后验均值，并采用期望‑最大化方法对未知参数进行迭代更新。与传统的单任务贝叶斯压缩感知算法相比，在获取的观测样本较少的情况下，本发明方法有着显著的性能提升。

技术研发人员：何振清,梁应敞
受保护的技术使用者：电子科技大学长三角研究院（湖州）
技术研发日：
技术公布日：2024/1/12