基于多标量乘快速计算的椭圆曲线验签方法及系统与流程

本发明涉及数字签名，特别是涉及基于多标量乘快速计算的椭圆曲线验签方法及系统。

背景技术：

1、本部分的陈述仅仅是提到了与本发明相关的背景技术，并不必然构成现有技术。

2、椭圆曲线密码(ecc)是一种公钥密码学算法，是近年来发展迅速的密码学分支，它基于数论中的椭圆曲线理论，能够在比基于离散对数问题的密码系统(如elgamal密码系统或dsa、rsa密码系统)的更小的有限域上构建椭圆曲线密码系统。在保持相同安全强度的情况下，ecc所需的密钥长度远小于基于离散对数问题的密码系统。因此，ecc相比于其他密码系统可以大大减少所需计算量、储存空间和数据流量等方面的开销。椭圆曲线算法是身份认证、密钥协商、区块链等应用的核心基础算法。

3、近年来，优化ecc中的标量乘法运算是许多学者研究的重要方向之一。目前有许多主流算法，例如倍点-点加二进制方法、非邻接表示形、带窗口的非邻接表示形等。这些算法的核心思想都是通过降低单标量的平均汉明密度来减少ecc中的额外运算。对于多标量乘法，联合稀疏形式jsf具有较低的汉明密度，且预计算量较非相邻格式naf小，如jsf-3的汉明重量约为0.54,jsf-5的汉明重量约为0.4,但是因为naf方法可以采用较大的窗口宽度，进一步减少总计算量，整体效率优于jsf方法。

4、提高公钥密码算法的计算速度是公钥密码算法的研究热点，椭圆曲线的多标量乘运算是椭圆曲线密码签名验签协议的基础构件，也是最耗时的部分。数字签名算法在实现数字签名和验签的过程中效率低下，浪费了计算机内部大量的计算资源，现有的数字签名算法的计算方式提高了时间的复杂度，数字签名算法在芯片上运行时，对芯片的功耗较大，数字签名过程速度慢，影响用户的使用体验。

技术实现思路

1、为了解决现有技术的不足，本发明提供了基于多标量乘快速计算的椭圆曲线验签方法及系统；通过对数字签名算法中遇到的多标量乘运算进行优化，大大降低了数字签名和数字验签过程的时间复杂度，数字签名算法在芯片上运行时，功耗较小，提升数字签名的运算速度，提升系统的整体性能，提升用户体验。

2、第一方面，本发明提供了基于多标量乘快速计算的椭圆曲线验签方法；

3、基于多标量乘快速计算的椭圆曲线验签方法，包括：椭圆曲线数字签名步骤和椭圆曲线签名验签步骤；所述椭圆曲线数字签名步骤和椭圆曲线签名验签步骤中的多标量乘计算过程包括：

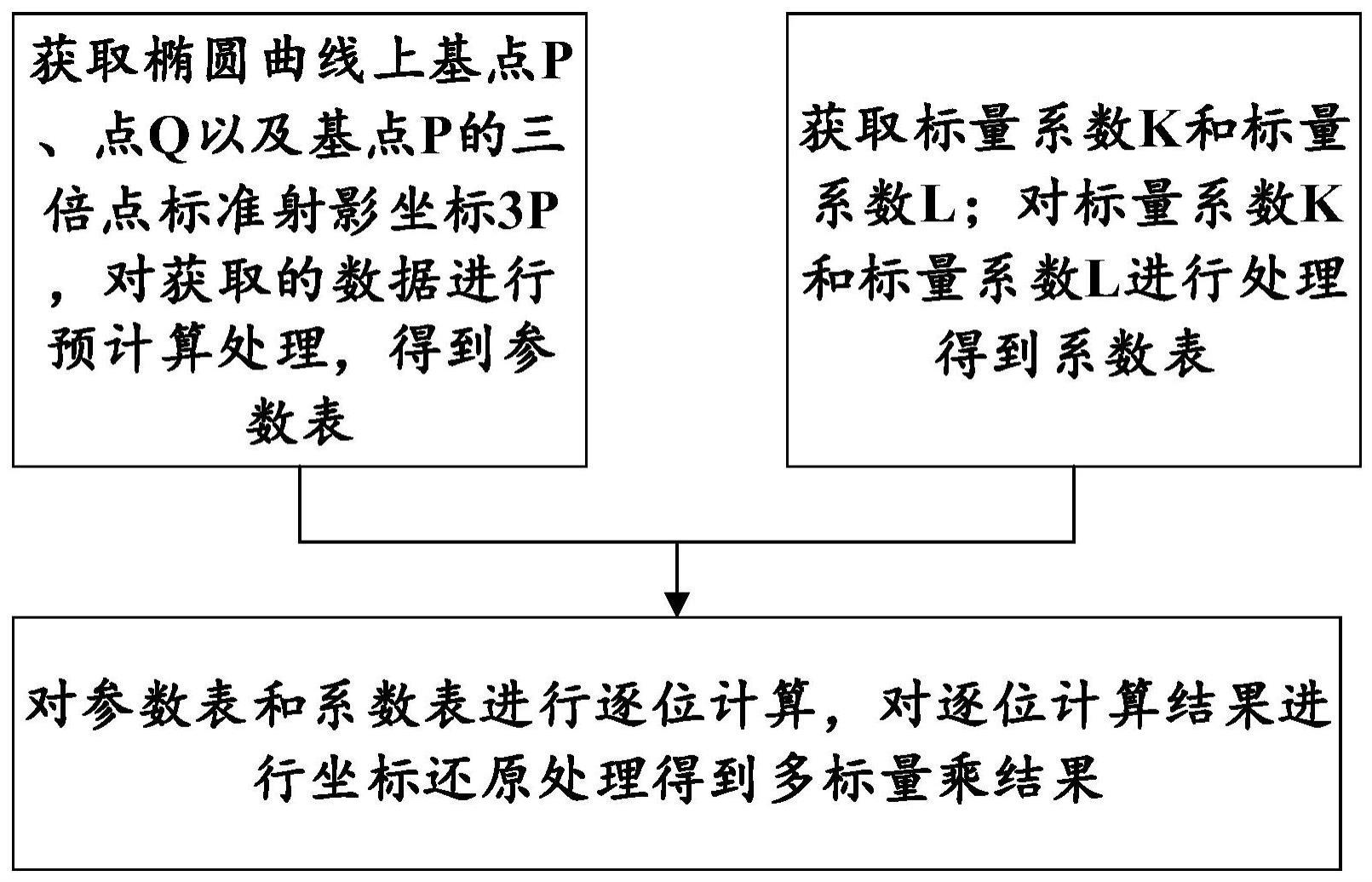
4、获取椭圆曲线上基点p、点q以及基点p的三倍点仿射坐标3p，对获取的数据进行预计算处理，得到参数表；

5、获取标量系数k和标量系数l；对标量系数k和标量系数l进行处理得到系数表；

6、对参数表和系数表进行逐位计算，对逐位计算结果进行坐标还原处理得到多标量乘结果。

7、第二方面，本发明提供了基于多标量乘快速计算的椭圆曲线验签系统；

8、基于多标量乘快速计算的椭圆曲线验签系统，包括：椭圆曲线数字签名模块和椭圆曲线签名验签模块；所述椭圆曲线数字签名模块和椭圆曲线签名验签模块中的多标量乘计算过程包括：

9、预计算单元，其被配置为：获取椭圆曲线上基点p、点q以及基点p的三倍点仿射坐标3p，对获取的数据进行预计算处理，得到参数表；

10、处理单元，其被配置为：获取标量系数k和标量系数l；对标量系数k和标量系数l进行处理得到系数表；

11、逐位计算单元，其被配置为：对参数表和系数表进行逐位计算，对逐位计算结果进行坐标还原处理得到多标量乘结果。

12、与现有技术相比，本发明的有益效果是：

13、通过对数字签名算法中遇到的多标量乘运算进行优化，大大降低了数字签名和数字验签过程的时间复杂度，数字签名算法在芯片上运行时，功耗较小，提升数字签名的运算速度，提升系统的整体性能，提升用户体验。

14、本发明提出了一种基于jsf和模逆的多标量乘法坐标预计算实现方法，近年来椭圆曲线模逆算法发展迅速，算法实现速度已经减少到了数千个时钟周期，因此可以利用五元联合稀疏表示jsf-5算法预计算量较少且汉明重量较低的特点，通过将预计算曲线点坐标从jacobian加重射影坐标系(x,y,z)转换到仿射坐标系(x,y)，大幅度降低多标量乘法执行过程中点加add的运算量，由12个模乘法m、4个模乘方s和7个简单模运算a,减少为8个模乘法m、3个模乘方s和7个简单模运算a。此外与倍点运算double组合，进一步降低计算复杂度，与现有技术相比，本发明具有速度快、内存和存储占用少等优势。

技术特征：

1.基于多标量乘快速计算的椭圆曲线验签方法，其特征是，包括：椭圆曲线数字签名步骤和椭圆曲线签名验签步骤；所述椭圆曲线数字签名步骤和椭圆曲线签名验签步骤中的多标量乘计算过程包括：

2.如权利要求1所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，获取椭圆曲线上基点p、点q以及基点p的三倍点仿射坐标3p，对获取的数据进行预计算处理，得到参数表，具体包括：

3.如权利要求2所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，所述设定坐标索引，是根据五元联合稀疏表示算法jsf-5，设定若干个不重复的常数，用于定位和辅助运算；

4.如权利要求2所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，所述基于坐标索引，计算基点p和点q的倍点和点加坐标，包括：

5.如权利要求2所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，所述基于基点p和点q的倍点和点加坐标，进行模逆运算，具体包括：设定6个256比特数t、t0、t1、t2、t3和t4用于存储中间变量；

6.如权利要求2所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，所述基于模逆运算结果，将各点坐标恢复到仿射坐标系，包括：

7.如权利要求6所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，z1＝t3.t3；z2＝z1.t3；

8.如权利要求1所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，所述对参数表和系数表进行逐位计算，对逐位计算结果进行坐标还原处理得到多标量乘结果，具体包括：

9.如权利要求8所述的基于多标量乘快速计算的椭圆曲线验签方法，其特征是，所述将计算结果由jacobian加重射影坐标系，转换为仿射坐标系，包括：

10.基于多标量乘快速计算的椭圆曲线验签系统，其特征是，包括：椭圆曲线数字签名模块和椭圆曲线签名验签模块；所述椭圆曲线数字签名模块和椭圆曲线签名验签模块中的多标量乘计算过程包括：

技术总结
本发明涉及数字签名技术领域，公开了基于多标量乘快速计算的椭圆曲线验签方法及系统；其中方法包括：椭圆曲线数字签名步骤和椭圆曲线签名验签步骤；椭圆曲线数字签名步骤和椭圆曲线签名验签步骤中的多标量乘计算过程包括：获取椭圆曲线上基点P、点Q以及基点P的三倍点仿射坐标3P，对获取的数据进行预计算处理得到参数表；对标量系数K和标量系数L进行处理得到系数表；对参数表和系数表进行逐位计算，对逐位计算结果进行坐标还原处理得到多标量乘结果。通过对数字签名算法中遇到的多标量乘运算进行优化，大大降低了数字签名和数字验签过程的时间复杂度，提升数字签名的运算速度，提升系统的整体性能，提升用户体验。

技术研发人员：付勇,陈鑫泽,王坤,高绍锋,陈丽娟,杨光,王继志,赵大伟,吴晓明,杨美红,王英龙
受保护的技术使用者：山东省计算中心（国家超级计算济南中心）
技术研发日：
技术公布日：2024/1/14