一种基于分布估计算法的子集选择方法

本发明涉及传感器网络部署，具体涉及一种基于分布估计算法的子集选择方法。

背景技术：

1、子集选择问题广泛存在于诸多技术领域，旨在寻找一个集合中的子集合，以使得某性能指标最优。例如，在机器学习领域中，往往需要进行特征选择，确定特征空间的子特征集合，以更高效、更优地进行机器学习模型的训练。再者，在传感器网络部署领域中，往往需要在预设部署点集合中选择数个部署点，部署一定数量的传感器，以最大化覆盖某个区域。

2、传感器网络部署领域是一个研究热点，在军用侦察、民用安防摄像头监视等领域有广泛应用。传感器网络部署领域中，一类实际问题需要在预设部署点集合选择数个部署点，部署一定数量的传感器，以更好地探测某个区域。这可以被认为是一个子集选择问题，子集选择问题就是在一个全集中选择一个固定大小的子集，对于传感器网络部署问题，预设的部署点集合即为全集，所选取的固定大小的子集即为用于部署传感器的点，因此对应传感器网络部署的子集选择问题即为：在预设的部署点集合中选择一个固定大小下的子集，该子集即对应一定数量的传感器，利用该子集进行传感器的部署。

3、子集选择问题一般而言是np困难(non-deterministic polynomial-timehardness,np-hardness)的，其求解不易。子集选择问题受到了许多研究者的关注。最经典的研究成果之一是冯·诺依曼理论奖得主、美国工程院院士george nemhauser等在1978年给出的结论：当目标函数f满足“单调性”和“次模性”时，贪心算法可获得(1-1/e)的近似比，且该近似比是最优多项式时间近似比。然而，在实际应用问题中，目标函数f往往是非线性的和非凸性的，甚至无法显示表达，并不具备良好的数学性质。

4、对于传感器网络部署方面，有一些学术研究，主要基于遗传算法、粒子群算法等实现部署方案。然而，子集选择问题往往要求从集合中选择固定大小的子集合。遗传算法的交叉、变异算子，粒子群算法的速度更新策略等，很容易破坏固定大小这一特性。贪心算法也并不适用于解决这一问题，因为传感器网络部署问题的目标函数往往是非凸性、非线性的，并不具备良好的数学性质。

5、目前尚未有技术方案能够在面对传感器网络部署问题中涉及的复杂目标函数时，实现有效的子集选择。

技术实现思路

1、有鉴于此，本发明提供了一种基于分布估计算法的子集选择方法，能够有效地从集合中选择出子集合，以最优化传感器网络部署问题中的复杂目标函数。

2、为达到上述目的，本发明的技术方案为：针对二维传感器网络部署问题，其中预设部署点数量为d，传感器的数量为q,q小于d，二维传感器网络部署问题的最终目标是在d维中选出q维，即进行子集选择；子集选择方法包括如下步骤：

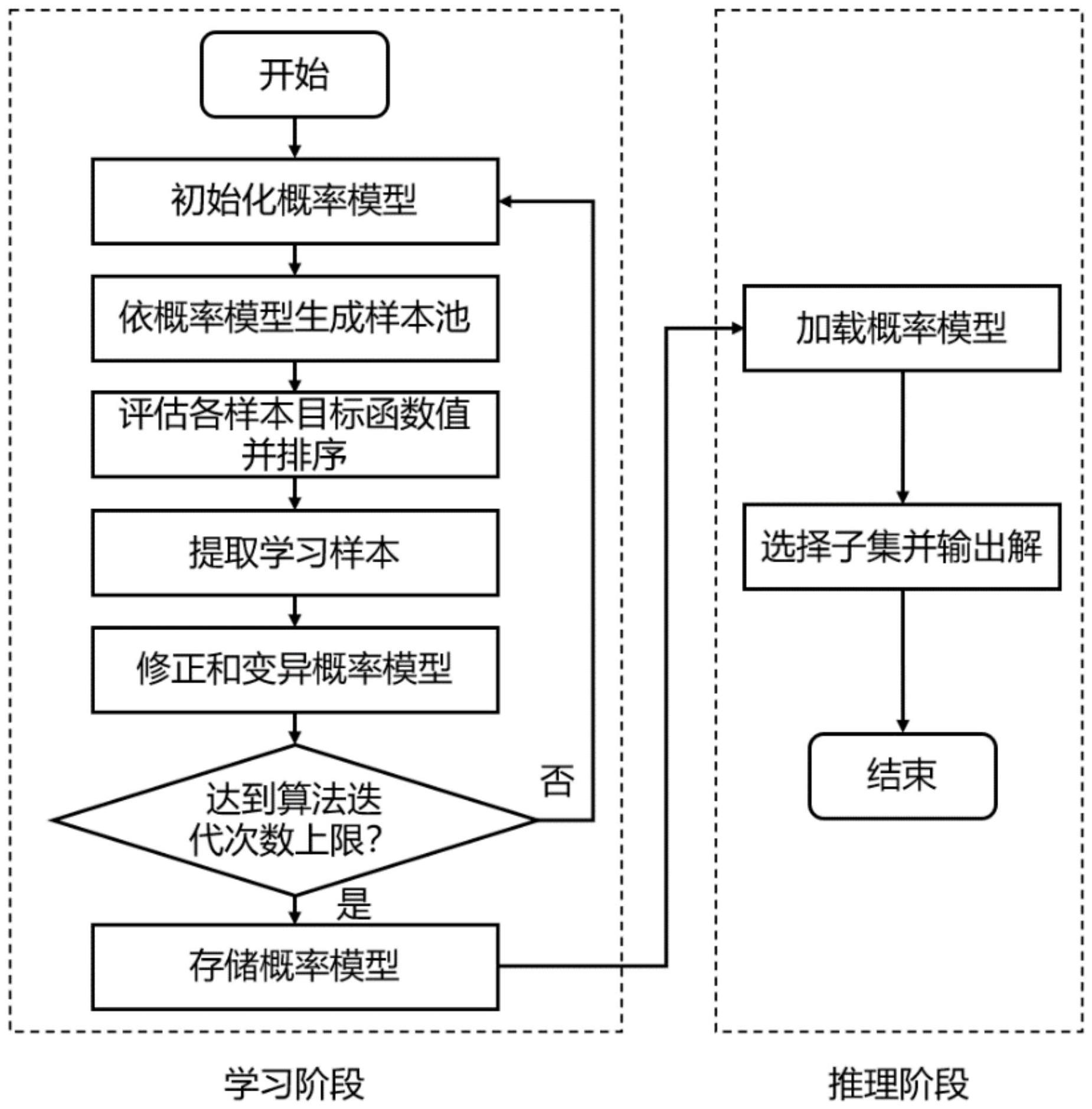
3、步骤一：初始化概率模型m，其维数为d；其中预设部署点集合对应于一个维数为d的概率模型m，d为预设部署点数量；每一维对应的概率值在(0,1)区间，用于表示对应部署点被部署一个传感器的概率。

4、步骤二：依概率模型m生成规模为p的样本池，其中每个样本对应一个解，维数为d。

5、步骤三：评估样本池中所有样本的目标函数值。

6、步骤四：对于最大化优化问题，根据目标函数值，对样本池中的样本进行降序排列，从样本池中提取以学习更新概率模型的样本比率为r。

7、步骤五：应用步骤四提取的学习样本更新概率模型m。

8、步骤六：判断算法迭代次数是否到达预设的迭代次数上限t，若到达，则终止方法并存储概率模型m；否则转入步骤二。

9、步骤七：利用最终得到的概率模型m输出最终的子集，通过查询子集中的元素在二维区域中确定传感器的部署点。

10、进一步地，步骤二：依概率模型m生成规模为p的样本池，其中每个样本对应一个解，维数为d；具体为：

11、对于每个样本，生成一个维数为d的0-1之间的随机分布，依次比较该随机分布与概率模型m每一位的值，若前者值小于后者，将当前样本的相应维度置为1；否则置0。

12、进一步地，步骤三：评估样本池中所有样本的目标函数值，具体地：

13、对于每个样本，生成一个辅助向量temp，其维数为d，各维度值均为0；取样本中值最大的k维，并将temp对应维度置1；具体地，样本中所有为1的维数被选中；若为1的维数小于k，则再选择样本中为0的下标索引最大的维数，直至被选择的维数达到k；

14、目标函数计算模块输入设置为temp，temp作为目标函数的输入，根据不同实际问题需要计算目标函数值。

15、进一步地，步骤三中，目标函数计算模块的具体实现为：

16、构造one-max问题的一个变种问题，其目标函数为

17、

18、其中为d＝100维的0-1二值决策向量，emp作为目标函数的输入由此分析出，当向量的第6-10、20-24、54-58和96-100维度的值为1时，该目标函数取得最大值，也是最优值；同时，若其他维度均为0，则子集选择更为直接。

19、进一步地，步骤四，对于最小化优化问题，可对目标函数值取负数以转化为最大化优化问题。提取目标函数值最大的个样本作为学习样本(learning samples)，其中表示向下取整操作。

20、进一步地，步骤五，应用步骤四提取的学习样本更新概率模型m，其中更新过程具体包括修正和变异；

21、修正和变异过程通过循环，依次利用所有学习样本对概率模型m进行更新；每次修正过程的数学形式为

22、pi←pi×(1.0-lr)+pi×lr  (1)

23、其中，pi表示概率模型m第i维的概率值，i∈1，...，d；式(1)中符号←左侧表示更新后的pi，右侧表示更新公式；lr表示设定的学习率；pi表示第p样本的第i维的值，p∈1，...，p，i∈1，...，d；

24、进一步地，在0-1之间随机生成一个浮点数；若该数小于设定的变异概率mutprob，则进行变异，每次变异过程的数学形式为

25、pi←pi×(1.0-mutshift)+random(0.0or1.0)×(mutshift)  (2)

26、其中，pi表示概率模型m第i维的概率值，i∈1，...，d；式(2)中符号←左侧表示变异后的pi，右侧表示变异公式；random(0.0or1.0)表示生成一个随机数，其值为0或1；mutshift表示设定的变异量。

27、有益效果：

28、本发明通过改进分布估计算法，使其可以有效解决传感器网络部署问题中的复杂目标函数下的子集选择问题，对诸多实际应用问题如机器学习特征选择、传感器网络部署等有益。本发明提供的方法可以较高效地进行搜索与优化，学习到所需的解空间信息。同时，该方法可以自动地学习到一个稀疏的概率模型，这有利于决策者直接进行子集选择。

技术特征：

1.一种基于分布估计算法的子集选择方法，其特征在于，针对二维传感器网络部署问题，其中预设部署点数量为d，传感器的数量为q，q小于d，所述二维传感器网络部署问题的最终目标是在d维中选出q维，即进行子集选择；所述子集选择方法包括如下步骤：

2.如权利要求1所述的一种基于分布估计算法的子集选择方法，其特征在于，所述步骤二：依概率模型m生成规模为p的样本池，其中每个样本对应一个解，维数为d；具体为：

3.如权利要求1所述的一种基于分布估计算法的子集选择方法，其特征在于，所述步骤三：评估样本池中所有样本的目标函数值，具体地：

4.如权利要求3所述的一种基于分布估计算法的子集选择方法，其特征在于，所述步骤三中，目标函数计算模块的具体实现为：

5.如权利要求1所述的一种基于分布估计算法的子集选择方法，其特征在于，所述步骤四，对于最小化优化问题，可对目标函数值取负数以转化为最大化优化问题。提取目标函数值最大的个样本作为学习样本(learning samples)，其中表示向下取整操作。

6.如权利要求1所述的一种基于分布估计算法的子集选择方法，其特征在于，所述步骤五，应用步骤四提取的学习样本更新概率模型m，其中更新过程具体包括修正和变异；

技术总结
本发明公开了一种基于分布估计算法的子集选择方法，涉及传感器网络部署技术领域。具体方案为：初始化概率模型；依概率模型生成规模为P的样本池；评估样本池中所有样本的目标函数值；对于最大化优化问题，根据目标函数值，对样本池中的样本进行降序排列，从样本池中提取以学习更新概率模型的样本比率；应用学习样本更新概率模型；重复上述过程直至达到预设的迭代次数上限，利用最终得到的概率模型M输出最终的子集，通过查询该子集中的元素在二维区域中确定传感器的部署点。本发明通过改进了分布估计算法，使得其可以有效解决复杂目标函数下的子集选择问题，对诸多实际应用问题如机器学习特征选择、传感器网络部署等有益。

技术研发人员：陈晨,张云天,田育萌,吴桐雨,沈元初,陈杰
受保护的技术使用者：北京理工大学
技术研发日：
技术公布日：2024/1/16