一种基于覆盖满意度最优的区域覆盖卫星星座设计方法

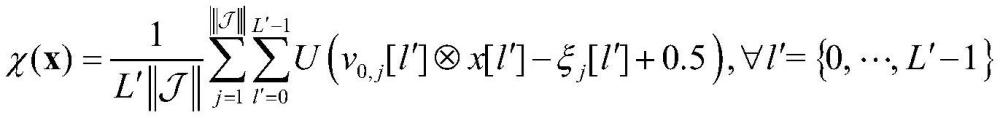
本发明属于卫星通信，尤其涉及一种基于覆盖满意度最优的区域覆盖卫星星座设计方法。

背景技术：

1、目前传统的卫星星座设计方法分为解析法和优化法。解析法往往将星座的几何结构与stk软件模拟的覆盖情况相结合进行建模；然而，由于星座设计的目标不是唯一的，且多为非线性、不连续的，传统的解析法不利于找到全局最优解。针对单目标优化问题，传统的优化法往往采用遗传算法，针对特定的系统目标进行星座设计，但其收敛速度缓慢，且难以收敛到全局最优解；针对多目标优化问题，以往工作采用非支配排序遗传算法求解在实际约束下制定的多目标优化问题，但是优化结果仅为帕累托最优集，仍需人工主观选取优化结果作为设计方案，存在一定主观性。

技术实现思路

1、发明目的：为了解决上述现有技术存在的问题，本发明公开了一种基于覆盖满意度最优的区域覆盖卫星星座设计方法。

2、技术方案：本发明提供了一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，包括如下步骤：

3、步骤1：计算共地面轨迹星座的星座平均覆盖满意度χ(x)，其中x为星座分布向量，x＝(x[0],x[1],…,x[l],…,x[l-1])t，l表示所有离散时刻个数，l表示第l个离散时刻，x[l]表示卫星相对于种子卫星间隔l个离散时刻的时移位置点，x[l]的表达式如下所示：

4、

5、lk表示第k颗卫星的时延指数；

6、步骤2：基于星座平均覆盖满意度，并以感兴趣区域的最小瞬时满意度作为约束条件，建立基于平均覆盖满意度最大的优化模型m1；

7、步骤3：将模型m1转化为解耦的模型m2，再将m2模型转换为标准0-1整数的优化模型m3；

8、步骤4：求解m3，得到最优的星座分布向量。

9、进一步的，所述步骤1中的共地面轨迹星座满足如下条件：

10、1、每颗卫星的轨道周期是格林威治节点周期的有理倍数；

11、2、所有卫星轨道在初始时刻的半长轴a、离心率e、倾角i和近地点幅角ω0均相同；

12、3、第k颗卫星的升交点赤经ωk和平近点角mk满足：

13、npωk+ndmk＝constant mod(2π)，

14、其中，nd是卫星格林威治节点周期数量，np是轨道周期数量，constant表示常数，mod表示余数。

15、进一步的，所述步骤1中的星座平均覆盖满意度χ(x)的表达式如下所示：

16、

17、其中，l′表示所有地面站有通信需求的离散时刻总数，表示感兴趣的区域中地面站集合，表示目标区域的地面站总数，u(·)表示单位阶跃函数，ξj[l′]表示第j个地面站在第l′个地面站有通信需求的离散时刻的卫星覆盖层数，v0,j[l′]表示种子卫星和第j个地面站之间在第l′个地面站有通信需求的离散时刻的接入函数，第k个卫星和第j个地面站之间在第l个离散时刻的接入函数的表达式入下所示：

18、

19、其中，当k＝0时表示种子卫星，θk,j[l]是第k颗卫星和第j个地面站之间在第l个离散时刻的仰角，θk,j,min[l]为在离散时间l时刻卫星k和地面站j之间的最小仰角；表示循环卷积算子。

20、进一步的，所述步骤2中的优化模型m1的表达式如下所示：

21、

22、其中，k表示中间变量，kmax表示最大卫星数量，σ0[l′]表示感兴趣区域的最小瞬时满意度，σ[l′]表示感兴趣区域的瞬时满意度，ζ(x)表示地面站的平均覆盖层数，ζ0表用户要求的卫星星座达到最小平均覆盖层数，ζ(x)和σ[l′]的表达式如下所示：

23、

24、

25、其中，dj[l′]是l＝l′时的瞬时满意度dj[l]的值，dj[l]满足如下关系：

26、

27、其中，ξj[l]是第j个地面站在第l个离散时刻需求的卫星覆盖层，bj[l]是星座在第l个离散时刻对第j个地面站施加的覆盖函数，bj[l]的表达式为：

28、

29、其中，k表示卫星星座分布中卫星的总个数。

30、进一步的，将l个离散时刻的覆盖函数构成覆盖函数向量bj，bj的表达式为：bj＝(bj[0],bj[1],…,bj[l],…,bj[l-1])t，bj和星座分布向量x满足如下关系：

31、v0,jx＝bj

32、其中，v0,j表示接入循环矩阵，v0,j的表达式为：

33、

34、则bj[l]与x[l]满足如下阶跃耦合关系：

35、

36、进一步的，所述模型m3的表达式如下所示：

37、

38、其中，q是增广向量，qt＝[dt,xt]，d是瞬时覆盖满意度向量，01×l表示1×l维的全0矩阵，表示维的全1矩阵；a1、a2、a3、a4、a5、b1、b2、b3、b4和b5的表达式如下所示：

39、

40、

41、

42、

43、

44、其中，i表示单位矩阵，i的下标表示单位矩阵的维度，σ0是感兴趣区域的最小覆盖瞬时满意度向量，满足σ0＝(σ0[0],…,σ0[l′],…,σ0[l′-1])t，是循环接入矩阵中去除空闲时刻接入函数后的新循环接入矩阵，vj(l′-1)+l′+1是第j个地面站在第l′个时刻的接入函数矩阵，vj(l′-1)+l′+1为循环接入矩阵v0,j的第j(l′-1)+l′行，ξj＝(ξj[0],…,ξj[l′],…,ξj[l′-1])t，m和ε皆为常数。

45、进一步的，所述模型m2的表达式如下所示：

46、

47、其中，m和ε皆为常数，q是增广向量，qt＝[dt,xt]，d是瞬时覆盖满意度向量，

48、进一步的，所述步骤4采用bilp法进行求解。

49、有益效果：本发明基于地面站的接入函数、覆盖需求函数、覆盖函数以及卫星的星座分布向量，建立系统的平均覆盖层数和平均覆盖满意度指标模型；针对这两个指标的同时优化，建立了以最大化平均覆盖满意度为目标、以平均覆盖层数达到设定值为约束的区域覆盖星座设计模型；在所述优化求解阶段，利用big-m法解耦原始模型，将原星座设计模型转化为标准0-1整数优化模型，再利用bilp法进行求解，最优解即为最优卫星星座。采用本发明方法，相比于传统设计方案，采用物理意义更强的指标进行单目标优化建模，无需采用多目标优化算法，且模型比传统方案更具有普适性。

技术特征：

1.一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，包括如下步骤：

2.根据权利要求1所述的一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，所述步骤1中的共地面轨迹星座满足如下条件：

3.根据权利要求1所述的一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，所述步骤1中的星座平均覆盖满意度χ(x)的表达式如下所示：

4.根据权利要求3所述的一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，所述步骤2中的优化模型m1的表达式如下所示：

5.根据权利要求4所述的一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，将l个离散时刻的覆盖函数构成覆盖函数向量bj，bj的表达式为：bj＝(bj[0],bj[1],…,bj[l],…,bj[l-1])t，bj和星座分布向量x满足如下关系：

6.根据权利要求5所述的一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，所述模型m3的表达式如下所示：

7.根据权利要求4所述的一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，所述模型m2的表达式如下所示：

8.根据权利要求1所述的一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，其特征在于，所述步骤4采用bilp法进行求解。

技术总结
本发明公开了一种基于覆盖满意度最优的区域覆盖卫星星座设计方法，基于地面站的接入函数、覆盖需求函数、覆盖函数以及卫星的星座分布向量，建立系统的平均覆盖层数和平均覆盖满意度指标模型；针对这两个指标的同时优化，建立了以最大化平均覆盖满意度为目标、以平均覆盖层数达到设定值为约束的区域覆盖星座设计模型；在所述优化求解阶段，利用BIG‑M法解耦原始模型，将原星座设计模型转化为标准0‑1整数优化模型，再利用BILP法进行求解，最优解即为最优卫星星座。采用本发明方法，相比于传统设计方案，采用物理意义更强的指标进行单目标优化建模，无需采用多目标优化算法，且模型比传统方案更具有普适性。

技术研发人员：陈明,刘江涛
受保护的技术使用者：东南大学
技术研发日：
技术公布日：2024/12/30