PET散射校正的方法与流程

本发明涉及医疗器械领域，尤其涉及一种正电子发射计算机断层扫描(PositronEmissionTomography，PET)散射校正的方法。

背景技术：
正电子发射计算机断层扫描(PositronEmissionTomography，PET)是一种利用向生物体内部注入正电子放射性同位素标记的化合物，而在体外测量它们的空间分布和时间特性的三维成像无损检测技术，具有灵敏度高、准确性好、定位准确的特点。PET的工作原理为：将发射正电子的放射性核素标记到能够参与人体组织血流或代谢过程的化合物上，将标有带正电子化合物的放射性核素注射到受检者体内，让受检者在PET的有效视野范围内进行PET显像。在PET扫描过程中，放射核素发射出的正电子在体内移动大约1mm后与组织中的负电子结合发生湮灭辐射(即湮灭事件)，产生两个能量相等、方向相反的γ光子。由于两个γ光子在体内的路程不同，到达两个探测器的时间也有一定差别，如果在规定的时间窗内(例如0-15us)，位于响应线上的探头系统探测到两个互成180度(±0.25度)的光子时，构成一个符合事件，处理设备就会记录下响应的数据，原始数据通过图像重建技术，可获得所需要的图像。然而，PET的符合事件包括真符合、散射符合和随机符合事件。其中，散射符合事件指的是：如果有一个光子在被探测到之前至少发生一次康普顿(Compton)散射，则探测到的事件为散射符合。参考图1，示意出了PET散射符合事件的示意图。如图1所示，在H点发生了一个湮灭事件，产生了一对γ光子L和R，L光子通过路程HA而飞行至探测器A，被探测器A记录；然而R光子在飞行过程中遇到了散射点S，在散射点S处发生康普顿散射，从而改变了飞行方向，到达探测器B被探测器B所记录。因此，如果不考虑所述散射事件，PET扫描设备会认为所述湮灭事件发生在探测器A和探测器B所在的响应线上，如果以这样的数据直接进行图像重建，获得的图像不够准确。为了解决散射问题带来的图像不准确的问题，现有技术中发展了散射校正的方法，具体地，在散射校正过程中基于PET扫描时探测器获得的原始数据获得湮灭事件的信息，之后基于散射点的分布模拟在PET扫描过程中发生的散射符合事件，进而获得去除散射符合事件的校正后数据，之后基于所述校正后数据进行图像重建，以获得较为准确的图像。更多的关于散射校正的方法可参考公开号为CN102439626A的中国专利申请。然而，现有技术散射校正的方法不够准确。

技术实现要素：
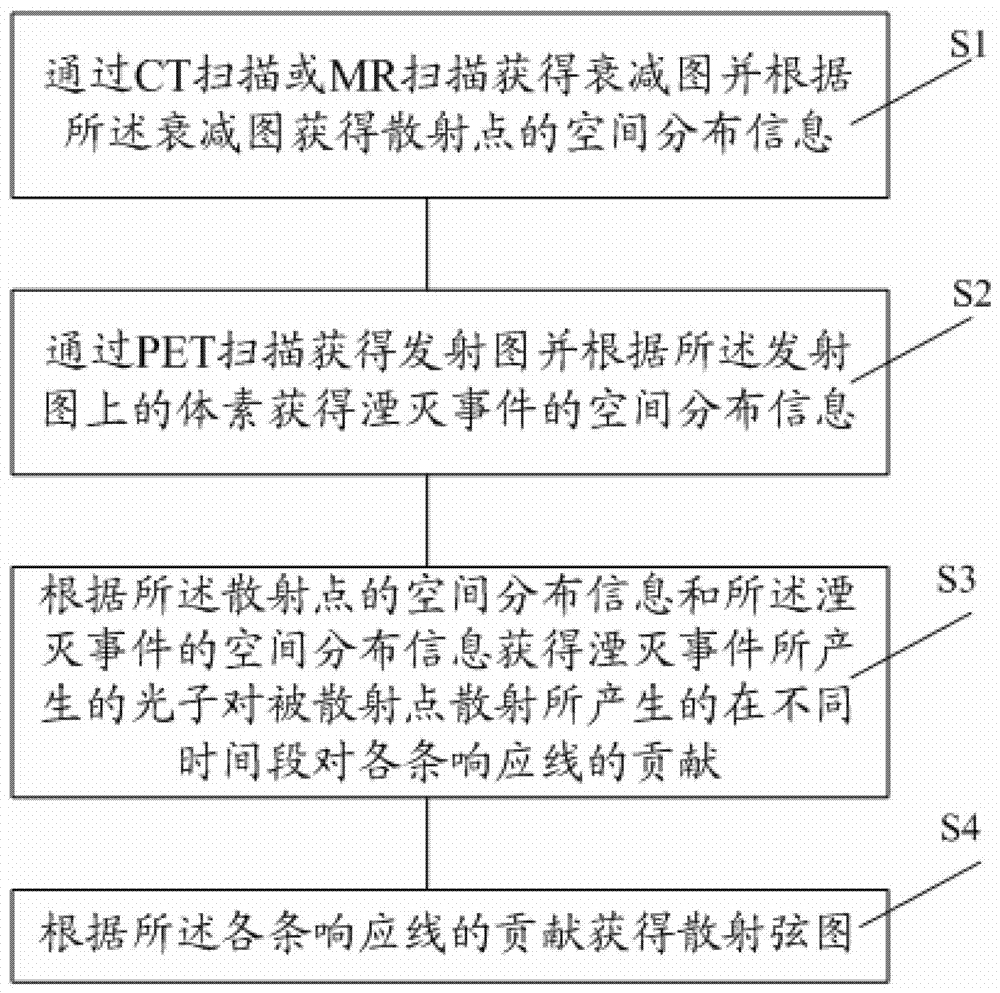
本发明的目的是提供一种较为准确的PET散射校正的方法。为了解决上述问题，本发明提供了一种PET散射校正的方法，包括：通过CT扫描或MR扫描获得衰减图并根据所述衰减图获得散射点的空间分布信息；通过PET扫描获得发射图并根据所述发射图上的体素获得湮灭事件的空间分布信息；根据所述散射点的空间分布信息和所述湮灭事件的空间分布信息获得湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条响应线的贡献；根据所述各条响应线的贡献获得散射弦图。可选地，所述贡献是通过对感兴趣区域内的所有散射点对响应线的贡献累加得出的。可选地，还包括如下步骤：结合所述散射点、所述湮灭事件发生点以及响应线两端的探测器所处的空间位置获得该湮灭事件所产生的光子对的飞行路程差。可选地，还包括如下步骤：结合所述飞行路程差获得飞行时间差，并通过真高斯核获得具有该飞行路程差的湮灭事件在不同时间段被记录的概率。可选地，所述获得湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条响应线的贡献是通过湮灭事件产生的光子对被散射点散射而产生的对响应线的贡献与光子对被PET扫描器记录到不同时间段的概率的乘积获得。可选地，所述湮灭事件产生的光子对被散射点散射而产生的对响应线的贡献是由对每一条响应线结合每一个散射点计算空间中发生湮灭事件的一对光子中的一个被该散射点散射一次所产生的被该响应线两端的探测器所记录下来的贡献获得的。可选地，所述光子对被PET扫描器记录到不同时间段的概率是通过如下步骤获得：根据产生湮灭事件的光子对中的两个光子各自的飞行路径，计算出该光子对的实际飞行路程差；根据响应线两端的探测器的时间段分装方式以及光速不变性获得以路程差为单位的各时间段的起始点；将光子的实际飞行路程差作为高斯函数的中点，以PET探测器系统的时间分辨率所对应的路程差为高斯函数的半高全宽，展开关于路程差的高斯函数；根据高斯函数的中点、半高全宽以及置信度寻找该高斯函数所覆盖的时间段范围；在所述时间段范围内计算每一时间段中所述高斯函数曲线下的面积，获得所述光子对被记录到该时间段的概率。可选地，展开的所述高斯函数曲线下的面积是根据高斯误差函数或互补误差函数获得的。可选地，所述高斯误差函数为其中x为路程差，t为时间。可选地，所述互补误差函数为其中x为路程差，t为时间。可选地，所述PET扫描的发射图是由对PET扫描所获得的发射弦图进行图像重建获得的。可选地，所述湮灭事件的空间分布信息是PET扫描的发射图的体素值。可选地，所述空间中的发生湮灭事件的位置是以PET扫描的发射图中被光线穿过的像素的边界在光线上所截取的线段的中点作为该像素中所有湮灭事件的发生点的位置。可选地，所述散射弦图由如下步骤获得：根据所有湮灭事件、所有散射点对同一响应线的贡献分别在不同时间段进行累加获得该响应线上各个时间段的贡献；组合所有响应线进而获得包含飞行时间差信息的散射弦图。与现有技术相比，本发明具有以下优点：结合飞行时间差，采用真高斯核获得PET扫描器记录的飞行时间差被分配到不同时间段的概率，更加真实地模拟了光子散射并被记录的过程，提高了PET散射校正的精度。附图说明图1是一种PET散射符合事件的示意图；图2是本发明PET散射校正方法的流程示意图；图3是图2中步骤S3获得光子对被PET扫描器记录到不同时间段的概率的流程示意图；图4是本发明PET散射校正的方法中探测器记录的路程差的示意图；图5是本发明PET散射校正的方法中路程差的高斯函数的示意图。具体实施方式在下面的描述中阐述了很多具体细节以便于充分理解本发明。但是本发明能够以很多不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似推广，因此本发明不受下面公开的具体实施的限制。其次，本发明利用示意图进行详细描述，在详述本发明实施例时，为便于说明，所述示意图只是实例，其在此不应限制本发明保护的范围。本发明提供一种PET散射校正的方法，在进行散射校正的过程中，结合湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条相应先的贡献，更准确地模拟了光子被散射点散射后被探测器探测的过程。参考图2，示出了本发明PET散射校正方法的流程示意图，所述PET散射校正的方法包括：步骤S1，通过CT扫描或MR扫描获得衰减图并根据所述衰减图获得散射点的空间分布信息；步骤S2，通过PET扫描获得发射图并根据所述发射图上的体素获得湮灭事件的空间分布信息；步骤S3，根据所述散射点的空间分布信息和所述湮灭事件的空间分布信息获得湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条响应线的贡献；步骤S4，根据所述各条响应线的贡献获得散射弦图。下面结合附图和具体实施例对本发明PET散射校正方法做详细说明。执行步骤S1，通过电子计算机X射线断层扫描(ComputedTomography，CT)或核共振(MagneticResonance，MR)扫描的方式获得衰减图(AttenuationMap,又叫μ-map)。根据所述衰减图中放射性射线的衰减情况可以获得散射点的空间分布信息。具体地，需要说明的是，如何获得散射点分布的方法与现有技术相同，在此不再赘述。请继续参考图1，示出了PET散射符合事件的示意图(图中仅以一个散射点S作为说明)。根据衰减图获得的空间分布信息可以获知散射点S的位置，进而可以模拟散射点S对光子的散射过程。步骤S2，通过PET扫描获得发射图并根据所述发射图上的体素获得湮灭事件的空间分布信息。请继续参考图1，患者或者被成像对象10放置于PET扫描器中，所述PET扫描器具有围绕患者或者被成像对象10的扫描环11，所述扫描环11设置有若干对探测器(例如探测器A、B)。在PET扫描过程中，对于真符合湮灭事件，放射核素发射出的正电子与在患者或被成像对象10中的负电子结合发生湮灭事件，产生由两个能量相等、方向相反的γ光子构成的光子对。具体地，在AB线上飞行的方向相反的γ光子可以被探测器A、B探测，AB构成响应线(LineofResponse，LOR)。如果探测器A、B记录到的γ光子的时间差位于规定的时间窗内，可以推得在AB响应线上发生了湮灭事件。因而，根据PET扫描获得的发射图上的体素可获得湮灭事件的空间分布信息。具体地，所述湮灭事件的空间分布信息是PET扫描的发射图的体素值，但是本发明对此不作限制。实际应用中，所述PET扫描的发射图是由对PET扫描所获得的发射弦图进行图像重建获得的，发射弦图进行图像重建的方法与现有技术相同，在此不再赘述。执行步骤S3，根据所述散射点的空间分布信息和所述湮灭事件的空间分布信息获得湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条响应线的贡献。具体地，所述湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条响应线的贡献通过湮灭事件产生的光子被散射点散射而产生的对响应线的贡献与光子对被PET扫描器记录到不同时间段的概率的乘积获得的。下面结合图1说明散射对PET扫描获得的发射图的影响，在H点发生湮灭事件，产生γ光子对。其中一个γ光子被探测器A探测并且记录，另一个γ光子因在散射点S处发生康普顿散射而改变方向，进而被探测器B探测并记录。在PET扫描过程中，除了真符合湮灭事件之外，还会发生散射符合事件。因此需要对PET扫描获得的发射图进行散射校正。实际上，如果H点发生的是真符合湮灭事件，会对AC响应线做出贡献，但是由于散射的原因，H点发生的散射符合事件被AB响应线记录，而对AB响应线记录的信息产生贡献。为了获得湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条响应线的贡献，需要模拟散射点对光子散射并被探测器记录的过程，进而对探测器记录到的数据进行校正。具体地，本实施例中，以单散射模拟(SingleScatterSimulation，SSS)为例模拟散射的过程，在SSS算法中，假设湮灭事件产生的一对光子的一个未被散射，而另一个光子被散射点散射一次，以模拟湮灭事件产生的光子被散射点散射的过程，从而计算出光子被散射后被响应线两端的探测器所记录下来的贡献(即对每一条响应线结合每一个散射点计算空间中发生湮灭事件的一对光子中的一个被该散射点散射一次所产生的被该响应线两端的探测器所记录下来的贡献)，以实现散射校正。需要说明的是，此处以SSS算法为例进行说明，但是本发明对此不作限制，在其他实施例中，还可以通过别的算法模拟散射过程。具体地，所述空间中的发生湮灭事件的位置是以PET扫描的发射图中被光线穿过的像素的边界在光线上所截取的线段的中点作为该像素中所有湮灭事件的发生点的位置，但是本发明对此不作限制。需要说明的是，可以在进行散射校正之前在散射点的空间分布中设置感兴趣的区域，所述获得所述贡献的过程可以通过对感兴趣区域内的所有散射点对响应线的贡献累加得出。请继续参考图1，以感兴趣区域中的一个散射为例进行说明，在SSS算法中，假设在空间某点H有一个湮灭事件，产生了一对γ光子L和R，各自飞行到达了探测器A和探测器B。具体地，可以结合所述散射点S、湮灭事件发生点(此处为H点出)以及响应线两端的探测器A、B所处的空间位置获得该湮灭事件所产生的光子对的飞行路程差，此处以Δx表示飞行路程差。由于γ光子的飞行速率相等且均为c，相应地，两个γ光子的飞行路程差与飞行时间差之间具有线性关系，具体地，以Δt表示飞行时间差，相应的Δt=Δx/c。因此基于两个探测器A、B记录的飞行路程差可以获得两个γ光子的飞行时间差。实际上，γ光子在被探测器记录的过程中包括：γ光子转换为可见光，之后可见光信号转换为电信号等的过程。因此，γ光子到达探测器A、B的时刻与γ光子被探测器A、B记录的时刻之间具有一定的延时，这使两个γ光子的真实飞行时间差Δt在被探测器记录时会产生一定的误差，以Δt’表示探测器A、B记录的飞行时间差，那么Δt’与Δt之间不是相等的关系。由于PET扫描中获得的是探测器记录的湮灭事件的时间差Δt’，为了准确地获得真实的飞行时间差Δt，需要获得Δt’与Δt之间的关系。本实施例中，Δt’近似为一个以Δt为中心，时间分辨率为半高全宽(FullWidthatHalfMaXimum)的正态分布，即探测器记录的飞行时间差Δt’对真实飞行时间差Δt进行了展宽。由于飞行路程差与飞行时间差之间为正比关系，因此相应地被探测器A、B记录的路程差Δx’近似为一个以真实路程差Δx为中心的正态分布，参考图4示出了的记录下来的路程差Δx’的示意图。其中横坐标为被探测器A、B记录的路程差Δx’，纵坐标为记录为某一路程差Δx’的概率。具体地，所述正态分布为高斯函数。基于步骤S1和步骤S2中以形成的散射点的空间分布信息、湮灭事件的空间分布信息，可获得真实路程差，基于真实飞行时间差和真实路程差的正比关系可获得真实飞行时间差。光子被探测器A、B记录时，真实飞行时间差被展宽，由响应线上两端的探测器进行记录，因此，基于上述信息可模拟湮灭事件所产生的光子被散射点散射所产生的对响应线的贡献，以便于进行散射校正。具体地，结合参考图1，以已知位置的湮灭事件发生点H形成的一对γ光子为例，在SSS算法中，H点产生的两个γ光子中的一个被S点散射后分别到达探测器A、B的真实路程差为ΔX＝SHA-(SHS+SSB)，相应地，真实飞行时间差为Δt＝[SHA-(SHS+SSB)]/c(其中SHA、SHS、SHB分别为湮灭事件发生点H与探测器A、散射点S、探测器B的路程)，两个γ光子中被探测器A、B记录的飞行时间差Δt’为以所述Δt为中心的高斯函数。优选地，通过真高斯核获得具有该飞行路程差的湮灭事件在不同时间段被记录的概率，可以提高散射校正的精度。实际PET系统进行探测的过程中，探测器A、B记录的飞行时间差通常被分装(rebin)为不同的时间段(timebin)。例如，具有6ns的符合时间窗(即Δt=6ns)的24个飞行时间差分装(n=24)具有250ps的时间段(τ=Δt/n=250ps)。为了准确地模拟γ光子被探测器A、B记录的过程，从而提高PET散射校正的精度，还需要结合飞行时间差，获得湮灭时间处产生的γ光子被散射后，在不同时间段对各响应线的贡献，进而更细致地模拟γ光子散射后实际被探测器记录的过程。因此，可以通过湮灭事件产生的光子对被散射点散射而产生的对响应线的贡献与光子对被PET扫描器记录到不同时间段的概率的乘积获得所述贡献。所述贡献也就是对每一条响应线结合每一个散射点计算空间中发生湮灭事件的一对光子中的一个被该散射点散射一次所产生的被该响应线两端的探测器所记录下来的贡献。请结合参考图3，示意出了获得图2中步骤S3中获得光子被PET扫描器记录到不同时间段的概率的流程示意图。步骤S31，根据产生湮灭事件的光子对中的两个光子各自的飞行路径，计算出该光子对的实际飞行路程差；步骤S32，根据响应线两端的探测器的时间段分装方式以及光速不变性获得以路程差为单位的各时间段的起始点；步骤S33，将光子的实际飞行路程差作为高斯函数的中点，以PET探测器系统的时间分辨率所对应的路程差为高斯函数的半高全宽，展开关于路程差的高斯函数；步骤S34，根据高斯函数的中点、半高全宽以及置信度寻找该高斯函数所覆盖的时间段范围；步骤S35，在所述时间段范围内计算每一时间段中所述高斯函数曲线下的面积，获得所述光子对被记录到该时间段的概率。具体地，下面结合附图对步骤S3进行详细说明。需要说明的是，此处仍然以SSS算法为例，但是本发明对此不做限制。执行步骤S31，结合参考图1，以已知位置的湮灭事件发生点H点形成的一对γ光子为例，在SSS算法中，H点产生的两个γ光子中的一个被S点散射后分别到达探测器A、B的真实路程差为ΔX＝SHA-(SHS+SSB)。执行步骤S32，根据响应线两端的探测器的时间段分装方式以及光速不变性获得以路程差为单位的各时间段的起始点。具体地，由于探测器A、B记录的飞行时间差通常被分装为不同的时间段，每个时间段的起止点对应于不同的飞行时间差，又由于飞行时间差和路程差之间具有线性关系(光速不变)，相应地，每个时间段的起止点对应于不同的路程差的起止点。本实施例中，结合路程差的起止点，通过真高斯核获得湮灭事件在不同时间段被记录的概率。执行步骤S33，将光子的实际飞行路程差作为高斯函数的中点，以PET探测器系统的时间分辨率所对应的路程差为高斯函数的半高全宽，展开关于路程差的高斯函数。参考图4，示出了探测器记录的路程差一实施例的示意图。图4中的半高全宽(FullWidthatHalfMaximum，FWHM)用于评价PET的系统分辨率。具体地，参考图5，示出了真实路程差X0为-200mm的湮灭事件被探测器A、B记录为某一路程差的高斯函数。本实施例以PET扫描系统的时间分辨率为400nm为例进行说明(时间分辨率决定高斯函数的半高全宽)。执行步骤S34，根据高斯函数的中点、半高全宽以及置信度寻找该高斯函数所覆盖的时间段范围，从而可以获得对应于每一时间段的起始点的位置。请继续参考图5，图中所示的横坐标为被探测器A、B记录的路程差，平行于纵坐标的直线对应为不同时间段的分割线，每一分割线均对应于一时间段的起止点位置。步骤S35，在所述时间段范围内计算每一时间段中所述高斯函数曲线下的面积，获得所述光子对被记录到该时间段的概率。为了获得湮灭事件在不同时间段对响应线的贡献，对于任一时间段而言，图5中位于分割线之间的路程差的高斯函数下的面积即为此事件被记录到此时间段的总概率。如图5所示，采用不同的阴影表示不同时间段高斯函数下的区域，例如对于真实路程差为X0的湮灭事件，被探测器A、B记录在起始位置X1和X2对应的时间段内的总概率为图5中位于X1和X2之间的高斯函数下区域的面积。本实施例中为了计算上述面积，采用高斯误差函数或互补误差函数来实现。具体地，所述高斯误差函数为所述互补误差函数为其中，x为路程差，t为时间。此处以互补误差函数为例说明计算上述面积的方法，具体地，指的是从起始点X2开始到正无穷的高斯函数下方的面积，而指的是从起始点X1开始到正无穷的高斯函数下方的面积。相应地，对于真实路程差为X0的湮灭事件，探测器记录的飞行时间差被分配到起始点为X1和X2所对应的时间段的概率为：其中，σ与PET系统时间分辨率的关系为所述FWHM为用于评价PET的系统分辨率的半高全宽。由此可见，本实施例结合路程差的高斯函数，通过真高斯核(非近似算法)获得在不同时间段被探测器A、B记录的概率。在获得PET扫描器记录的飞行时间差被分配到不同时间段的概率之后，基于湮灭事件产生的光子因散射而产生的对响应线的贡献、光子对被PET扫描器记录到不同时间段的概率的乘积，获得湮灭事件及散射点在不同时间段对响应线的贡献。请继续参考图1，为了获得湮灭事件产生的光子因散射而产生的对响应线的贡献，在实际应用中，可沿着AS线做光线追踪(RayTracing)，对于发射图中每一个被穿过的像素，以像素中心点作为湮灭事件的发生点H，计算出的真实路程差为ΔX＝SHA-(SHS+SSB)，此像素对于响应线AB的贡献为：其中是Ω(A，S)为从S点看探测器A的表面积的立体角大小，Ω(B，S)是从S点看探测器B的表面积的立体角大小，μ是物体对511keV的伽玛光子的线性衰减系数，σc为511keV时的康普顿散射总截面，为对应于散射角ASB的康普顿散射微分截面，ε为探测器效率，μ’是伽玛光子被散射后的线性衰减系数，ε’为伽马光子被散射后的探测器效率，λ正比于在患者或被成像对象10中湮灭事件发生次数，Vs为发射图的像素值，ds为线积分的线元。其中，M为系统矩阵，下标H和AB表示对应于像素H和响应线AB的矩阵元。需要说明的是，还可以采用类似地方法对BS进行光线追踪。具体地，基于所述与步骤S32获得的不同时间段被记录的概率P的乘积，可以获H点所在像素在不同时间段对响应线AB的贡献。执行步骤S4，根据所述各条相应线的贡献获得散射弦图。具体地，包括以下步骤：首先，根据所有湮灭事件、所有散射点对同一响应线的贡献分别在不同时间段进行累加获得该响应线上各个时间段的贡献；其次，组合所有响应线进而获得包含飞行时间差信息的散射弦图。具体地，按照类似地方法进行光线追踪，对各衍射点H(各像素)和散射点S在不同时间段对响应线AB的贡献进行累加()，完成一条响应线AB的计算。类似地，遍历完患者或者被成像对象10中的所有散射点，和弦图中所有需要计算的响应线，可以得到一幅完整的含飞行时间差的散射弦图。综上，本发明提供的PET散射校正的方法在进行散射校正的过程中，结合湮灭事件所产生的光子对被散射点散射所产生的在不同时间段对各条相应先的贡献，更准确地模拟了光子被散射点散射后被探测器探测的过程。此外，基于路程差的高斯误差函数或互补误差函数获得探测器记录的飞行时间差被分配到不同时间段的概率，与通过伪高斯核(Quasi-Gaussian)的近似计算相比，本发明采用了非近似的真高斯核进行的计算，更加真实的模拟了光子散射并被记录的过程，提高了PET散射校正方法的准确性。还有，在计算量上，假若PET系统记录了n个时间段，则对于某一事件被记录到某一时间段的概率计算，本发明只需要两次高斯误差函数或互补误差函数的计算即可，计算量较小；对于n越大，也即飞行时间差测量越准确的情况，本发明的计算量优势越明显。更进一步地，本发明中，不同时间段的散射弦图可以同时计算，对于时间测量越准确，计算散射弦图越多的情况，本发明的计算量的增长并不明显，与分别计算各时间段的弦图的方法而言，本发明PET散射校正的方法具有较少的计算时间。本发明虽然已以较佳实施例公开如上，但其并不是用来限定本发明，任何本领域技术人员在不脱离本发明的精神和范围内，都可以利用上述揭示的方法和技术内容对本发明技术方案做出可能的变动和修改，因此，凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化及修饰，均属于本发明技术方案的保护范围。