一种基于分组稀疏性的自适应心音信号去噪方法与流程

文档序号：11087804阅读：909来源：国知局

本发明属于生物信号处理的研究领域，具体涉及一种心音信号的自适应去噪方法，是一种心音信号增强的技术手段。

背景技术：

心音是人体一种重要的生理信号，承载着与人体健康状况有关的有价值的诊断信息。相关的专业人员可通过听诊的方式从心音中获取这些信息，并依据这些信息进行相应的决策或诊断。然而，无论是使用传统的心音听诊器还是使用现代的数字心音传感器或数字听诊器时，心音信号中都存在着大量干扰噪声。这些来源复杂的噪声损害了心音中有重要价值的信息，严重影响了心音信号的可用性，从而会导致使用这些信息的专业人员做出错误的决策或诊断。因而，需要对心音信息进行有效的降噪声处理。

为实现心音去噪的目的，小波变换是最常用的方法之一。小波变换需要预定义适当的基函数，使用“db10”、“db5”或“bior5.5”等基函数的小波变换是目前用于心音去噪的主要方法。然而，由于年龄、性别和身体状态等差别，心音这种弱信号生理信号具有不同的特征形态，小波变换中预定义的基函数很难很好地匹配心音的多样性。因此，这需要有更为适合心音信号特点的去噪方法。

技术实现要素：

本发明的目的在于基于心音信号一阶差分序列的分组稀疏特征，提供一种基于分组稀疏性的自适应心音信号去噪方法。

本发明基于国际公开的心音数据库的去噪实验表明，本发明中所提出的去噪方法远好于传统的小波变换去噪方法。

为了实现上述目的，本发明采取的技术方案如下：

步骤1：初始化参数

所提出算法的相关参数及输入量设置如下：

分组大小参数K：K＝20

其中K表示分组的大小；

伽马分布(Gamma)先验的形状参数：α＝1，

Gamma先验的尺度参数：β＝50

归整参数：θ＝0.8

算法中降噪信号的初始投影为x⁽⁰⁾＝y，其中y是长度为N的含噪声心音信号；

步骤2：更新正则化参数

在算法的第k次迭代过程中，正则参数λ^(k)依下式进行更新

式(1)中的变量说明：δ²是预估的噪声方差；α，β，θ是在步骤1中初始化的参数；N是信号的长度；x^(k)是算法在第k次迭代过程的投影；D是差分矩阵，其定义为

函数是差分序列Dx^(k)的分组稀疏性度量函数，其定义为：

其中[Dx^(k)]_n，K是差分序列Dx^(k)的第n个大小为K的分组，| ||₂表示向量的l₂范数；

步骤3：计算近似投影

依据在步骤2中所更新的正则参数λ^(k)，进而计算降噪心音信号的新的投影x^(k+1)，其计算过程由以下步骤构成，相关变量与符号的含义与步骤2中相同；

步骤3.1：

计算对角阵Λ_(t)，其对角元素按下式进行计算：

其中上角标^-1表示求逆运算；

步骤3.2：

计算中间变换矩阵F

其中I表示单位矩阵，上角标表示^T矩阵转置运算；

步骤3.3：

计算降噪心音信号新的投影

x^(t+1)＝Fy (6)

步骤4：降噪算法的停止条件

降噪算法的停止迭代为

||y-x^(k+1)||²≥Nδ² (7)

否则算法转到步骤(2)继续执行；

当算法依据条件(7)停止时，算法输出的x^(k+1)降噪后就是含噪声心音y经过降噪处理后的信号。

本发明的有益效果：本发明与目前广泛用于心音信号降噪的小波变换方法相比，所提出的降噪方法具有更好的降噪声效果和更低的计算代价。由于不需要任何预定义基函数，减少了算法所需的存储空间，而且算法易于实现。因此，本发明的技术方案具有易于实现、可靠性好的特点，因此适合推广使用。

附图说明

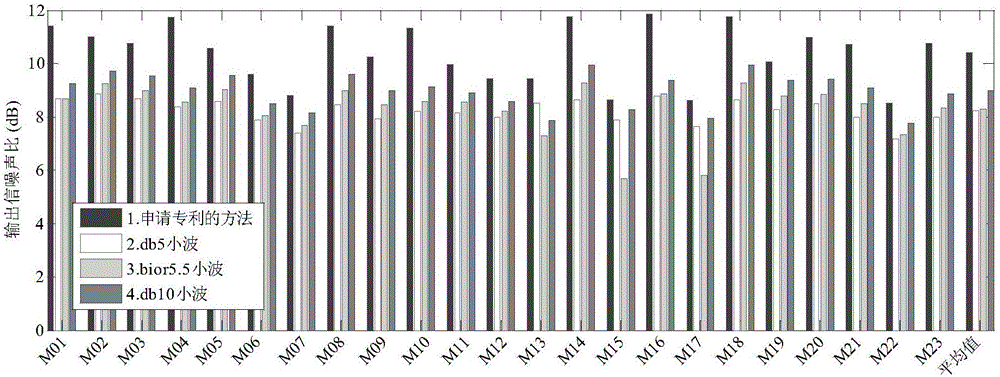
图1为采用现有的db10、db5、bior5.5三种小波变换降噪方法与本发明中所述的降噪方法，在输入含噪心音为-5dB时，对美国马里兰大学公开发布的心音数据库中的心音记录进行降噪处理时的性能表现及其平均性能表现图；

图2为采用现有的db10、db5、bior5.5三种小波变换降噪方法与本发明中所述的降噪方法，在输入含噪心音为5dB时，对美国马里兰大学公开发布的心音数据库中的心音记录进行降噪处理时的性能表现及其平均性能表现图。

具体实施方式

下面结合附图对本发明作进一步阐述。