基于朴素贝叶斯网络的病症与药物的匹配方法

：
1.本发明涉及生物医药技术领域，尤其涉及一种基于朴素贝叶斯网络的病症与药物的匹配方法。


背景技术：

2.在传统的中蒙医治疗过程中，医生需要根据自身所学为患者开具药方，但是，由于病症以及药材药效的复杂化和多样化，在对药物进行配伍开具药方时，对于医生的经验依赖程度较高，存在药物使用不合理的情况，这将直接影响患者的治疗效果，甚至会影响患者的健康。
3.目前，研究配方中药物与其治疗的病症关系的方法有很多，多数使用的是拆方分析法，如药对研究法、单味药研究法等。此类方法显然只能在控制其他药物不变的情况下，改变一味药物或两味药物，探究配方中的药物与病症之间的关系，对配方中治疗的病症进行一味或二味药物的研究，显然并不能精确地从整体角度上对配方中各治疗的病症和各味药物之间的非线性映射关系进行综合性研究，无法为医生开具药方提供参考依据，无法高效、有效的降低不合理用药的情况以及对于医生经验的依赖程度。


技术实现要素：

4.本发明的目的在于提供一种基于朴素贝叶斯网络的病症与药物的匹配方法，可为确定治疗方案提供参考依据，为医生推荐合理、有效、高效的药物，降低不合理用药的情况，降低对于医生经验的依赖程度，提高医生的工作效率。
5.本发明由如下技术方案实施：
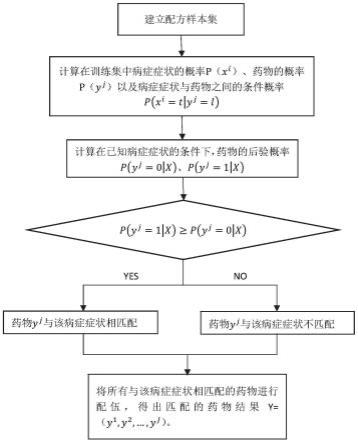
6.基于朴素贝叶斯网络的病症与药物的匹配方法，包括以下步骤：
7.s1、收集若干传统的配方，将配方对应的病症症状x与所使用的药物y相对应，形成配方样本集z；
8.s2、将所述s1中建立的配方样本集z中的部分配方作为训练配方集，并将所述训练配方集进行二值化处理后得到训练集，利用训练集对朴素贝叶斯网络模型进行训练，计算出训练集中病症症状的概率p(xi)、药物的概率p(yj)以及病症症状与药物之间的条件概率p(xi＝t|yj＝l)，t＝0，1表示病症症状xi不存在和存在两种情况，l＝0，1表示药物yj未使用和使用两种情况；
9.s3、将待开药病例的病症症状x’作为输入参数，根据所述s2中计算得到的病症症状的概率p(xi)、药物的概率p(yj)以及病症症状与药物之间的条件概率p(xi＝t|yj＝l)，计算出各味药物使用的后验概率p(yj＝1|x)和各味药物未使用的后验概率p(yj＝0|x)，其中，x＝(x1，x2，
…
，xi，
…
，xi)表示患者的各个病症症状，xi(i＝1，2，
…
，i)的取值为1或0；
10.s4、比较p(yj＝1|x)和p(yj＝0|x)的大小，若p(yj＝1|x)≥p(yj＝0|x)，则判断该味药物是与所述病例的病症症状x’相匹配的药物，将所有与所述病例的病症症状x’相匹配的药物进行配伍即得出匹配的药物结果y＝(y1，y2，...，yj)。
11.优选的，所述s1中，
12.配方样本集z＝{(x1，y1)，(x2，y2)，
…
，(xn，yn)，
…
，(xn，yn)}，
13.其中，n为配方样本集中的配方总数量；
14.第n首配方中对应的病症特征记作向量中的是第n首配方中对应的第i种病症症状；
15.第n首配方中的药物配伍记作向量中的是第n首配方中第j味药物。
16.优选的，所述s2包括以下步骤：对训练配方集进行二值化处理的方法为，在一首配方中，若病症症状xi存在，则对该病症症状xi赋值1；若病症症状xi不存在，则对该病症症状xi赋值0；同理，若开具的药方中有药物yj，则对该药物yj赋值1；若开具的药方中没有药物yj，则对该药物yj赋值0。
17.优选的，所述s2包括以下步骤：
18.(1)计算训练集中病症症状的概率p(xi)和药物的概率p(yj)，具体的，
[0019][0020]
在式(1)中，表示在训练集中病症症状xi＝t的累加频数，t＝0，1表示病症症状xi不存在和存在的两种情况，即t＝0表示第n首配方中病症症状xi不存在，t＝1表示第n首配方中病症症状xi存在，n为配方样本集中的配方总数量；
[0021][0022]
在式(2)中，表示在训练集中药物yj＝l的累加频数；l＝0，1表示药物yj不使用和使用的两种情况，即l＝0表示第n首配方中药物yj未使用，l＝1表示第n首配方中药物yj被使用，n为配方样本集中的配方总数量；
[0023]
(2)计算训练集中病症症状xi＝t且药物yj＝l时的概率p(xi＝t，yj＝l)，
[0024][0025]
在式(3)中，表示在训练集中病症症状xi＝t且药物yj＝l时的配方累加频数；
[0026]
(3)计算病症症状与药物之间的条件概率p(xi＝t|yj＝l)，
[0027]
[0028]
将式(2)和式(3)代入式(4)中即可求出条件概率。
[0029]
优选的，所述s3中：各味药物使用和未使用的后验概率p(yj＝l|x)的计算方法如下：
[0030][0031]
在式(5)中，x＝(x1，x2，
…
，xi，
…
，xi)表示患者的各个病症症状，xi(i＝1，2，
…
，i)的取值为1或0；l＝0，1表示药物yj的未使用和使用两种情况，即p(yj＝0|x)表示药物yj未使用的后验概率，即p(yj＝1|x)表示药物yj使用的后验概率。
[0032]
本发明的优点：
[0033]
本发明以病症症状(x1，x2，
…
，xi，
…
，xi)作为输入节点，每一个输入节点表示一种病症症状；以药物(y1，y2，
…
，yj，
…
，yj)作为输出节点，每一个输出节点表示一味药物；输入节点和输出节点之间的连接表示病症症状和药物之间的映射关系。病症症状节点与药物节点之间用条件概率进行表示，以条件概率体现各输入节点到输出节点之间的概率强度，条件概率越大则表明连接两端的病症症状与药物之间的相关性越强，即治疗该病症症状越适合使用该味药物。
[0034]
通过本发明，医生只需要确定患者的病症症状，将病症症状输入，即可输出匹配的药物结果，可为确定治疗方案提供参考依据，为医生推荐合理、有效、高效的药物，降低不合理用药的情况，降低对于医生经验的依赖程度，提高医生的工作效率。
附图说明：
[0035]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0036]
图1为本发明基于朴素贝叶斯网络的病症与药物的匹配方法的流程图；
[0037]
图2为本发明基于朴素贝叶斯网络的病症与药物的匹配方法的结构模型图。
具体实施方式：
[0038]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0039]
实施例1：
[0040]
如图1、图2所示的基于朴素贝叶斯网络的病症与药物的匹配方法，包括以下步骤：
[0041]
s1、收集24首传统的蒙医配方，将配方对应的病症症状x与所使用的药物y相对应，形成配方样本集
[0042]
z＝{(x1，y1)，(x2，y2)，
…
，(xn，yn
)
，
…
，(x
24
，y
24
)}，如表1所示。
[0043]
表1配方样本集
[0044]
[0045]
[0046]
[0047][0048]
表1中共涉及46种病症症状，78味药物。将所涉及的病症症状xi(i＝1，2，
…
，46)和药物yj(j＝1，2，
…
，78)列于表2。
[0049]
表2病症症状与药物
[0050][0051]
s2、将s1中建立的配方样本集z中的前22首作为训练配方集，如表3所示；后2首作为测试配方集。
[0052]
表3训练配方集
[0053]
[0054]
[0055][0056]
将表3训练配方集中的病症症状xi和药物yj进行数据二值化处理，即在一首配方中，若病症症状xi存在，则对该病症症状xi赋值1；若病症症状xi不存在，则对该病症症状xi赋值0；当时表示第i种病症症状在第n首配方中存在，即第n首配方中的药物配伍可治疗该病症症状；当时表示第i种病症症状在第n首配方中不存在，即第n首配方中的药物配伍未治疗该病症症状。同理，若开具的药方中有药物yj，则对该药物yj赋值1；若开具的药方中没有药物yj，则对该药物yj赋值0；当时表示第j味药物在第n首配方中使
用，当时表示第j味药物在第n首配方中未使用。最终形成如表4所示的训练集。
[0057]
表4训练集
[0058][0059]
利用训练集对朴素贝叶斯网络模型进行训练，计算出训练集中病症症状的概率p(xi)、药物的概率p(yj)以及病症症状与药物之间的条件概率p(xi＝t|yj＝l)，t＝0，1表示病症症状xi不存在和存在两种情况，l＝0，1表示药物yj未使用和使用两种情况；具体的，包括以下步骤：
[0060]
(1)计算训练集中病症症状的概率p(xi)和药物的概率p(yj)，具体的，
[0061][0062]
在式(1)中，表示在训练集中病症症状xi＝t的累加频数，t＝0，1表示病症症状xi不存在和存在的两种情况，即t＝0表示第n首配方中病症症状xi不存在，t＝1表示第n首配方中病症症状xi存在，n为配方样本集中的配方总数量；利用式(1)可计算各病症症状的不存在概率p(xi＝0)和各病症症状的存在概率p(xi＝1)。
[0063][0064]
在式(2)中，表示在训练集中药物yj＝l的累加频数；l＝0，1表示药物yj不使用和使用的两种情况，即l＝0表示第n首配方中药物yj未使用，l＝1表示第n首配方中药物yj被使用，n为配方样本集中的配方总数量；利用式(2)可计算各味药物的未使用概率p(yj＝0)和药物使用概率p(yj＝1)。
[0065]
(2)计算训练集中病症症状xi＝t且药物yj＝l时的概率p(xi＝t，yj＝l)，
[0066][0067]
在式(3)中，表示在训练集中病症症状xi＝t且药物yj＝l时的配方累加频数；
[0068]
利用式(3)可计算配方训练集中药物和病症症状分别处于不同情况下的概率，分别是p(xi＝1，yj＝1)，p(xi＝1，yj＝0)，p(xi＝0，yj＝1)和p(xi＝0，yj＝0)四部分概率。
[0069]
(3)计算病症症状与药物之间的条件概率p(xi＝t|yj＝l)，
[0070][0071]
将计算得到的数据p(yj＝1)和p(xi＝1，yj＝1)代入式(4)中，计算出训练集中药物使用与病症症状存在的条件概率p(xi＝1|yj＝1)；将计算得到的数据p(yj＝1)和p(xi＝0，yj＝1)代入式(4)中，计算出训练集中药物使用与病症症状不存在的条件概率p(xi＝0|yj＝1)；将计算得到的数据p(yj＝0)和p(xi＝1，yj＝0)代入式(4)中，计算出训练集中药物未使用与病症症状存在的条件概率p(xi＝1|yj＝0)；将计算得到的数据p(yj＝0)和p(xi＝0，yj＝0)代入式(4)中，计算出训练集中药物未使用与病症症状不存在的条件概率p(xi＝0|yj＝0)。
[0072]
s3、将待开药病例的病症症状x’作为输入参数，根据所述s2中计算得到的病症症状的概率p(xi)、药物的概率p(yj)以及病症症状与药物之间的条件概率p(xi＝t|yj＝l)，计算出各味药物使用的后验概率p(yj＝1|x)和各味药物未使用的后验概率p(yj＝0|x)，其中，x＝(x1，x2，
…
，xi，
…
，xi)表示患者的各个病症症状，xi(i＝1，2，
…
，i)的取值为1或0；
[0073]
各味药物使用和未使用的后验概率p(yj＝l|x)的计算方法如下：
[0074][0075]
在式(5)中，
[0076]
x＝(x1，x2，
…
，xi，
…
，xi)表示患者的各个症状症状，xi(i＝1，2，
…
，i)的取值为1或0。l＝0，1表示药物yj的未使用和使用两种情况，即p(yj＝0|x)表示药物yj未使用的后验概率，p(yj＝1|x)表示药物yj使用的后验概率。
[0077]
s4、比较p(yj＝1|x)和p(yj＝0|x)的大小，若p(yj＝1|x)≥p(yj＝0|x)，则判断该味药物是与所述病例的病症症状x’相匹配的药物，将所有与所述病例的病症症状x’相匹配的药物进行配伍即得出匹配的药物结果y＝(y1，y2，...，yj)。
[0078]
实验例1：
[0079]
将实施例1中测试配方集中的2首配方对应的病症症状，利用本发明方法来得出与其匹配的药物，进而验证传统配方中的药物配伍与由本发明方法给出的药物配伍一致性。其病症症状和药物配伍列于表5。
[0080]
表5测试配方集
[0081][0082]
将表5测试配方集中的病症症状xi和药物yj进行数据二值化处理，最终形成测试集。
[0083]
以测试集中的病症症状作为输入参数，根据实施例1的方法，首先，计算出病症症状的概率p(xi)、药物的概率p(yj)以及病症症状与药物之间的条件概率p(xi＝t|yj＝l)，再计算出使用某一药物的后验概率p(yj＝1|x)和不使用某一药物的后验概率p(yj＝0|x)。将同一药物对应的p(yj＝0|x)和p(yj＝1|x)进行比较，若p(yj＝1|x)≥p(yj＝0|x)则判断该病症症状下使用该药物，否则判断该病症症状下未使用该药物；最后，将所有判断该病症症状下使用的药物进行配伍即为利用本发明方法来得出与其匹配的药物结果y＝(y1，y2，...，yj)，结果列于表6。
[0084]
表6利用本发明方法来得出与其匹配的药物结果
[0085][0086]
将表5中的传统的药物配伍和表6中的利用本发明方法来得出与其匹配的药物结果相比较可知，序号2的两组药物配伍完全相同，序号1中，表5传统配方中共9味药物，而表6表利用本发明方法来得出与其匹配的药物结果共给出了10味药物，其中表6用栀子、川楝子和红花替换表5中的兔心和丁香。
[0087]
针对序号2中的病症症状，传统配方与本发明得到的匹配药物结果有所差别，因此进行下面的分析：
[0088]
根据实施例1中的式(5)可求出单一病症症状下使用单味药物的后验概率p(xi＝1|yj＝1)，即可反映出药物对病症症状的治疗效果。将p(xi＝1)、p(yj＝1)和p(xi＝1|yj＝1)的数据代入式(5)，求得单一病症症状和单味药物之间的后验概率p(yj＝1|xi＝1)，即得出单味药物的使用和未使用的情况，结果如表7所示。
[0089]
表7单味药物的使用和未使用的情况
[0090][0091]
在表7中所列的病症症状为序号2中出现的病症症状，可以看出各味药物对各种病症症状的治疗效果。由表7可知在治疗心悸方面，在传统配方的药物配伍中丁香和兔心比栀子、川楝子和红花的效果好；而在胸刺痛方面，栀子和川楝子治疗效果比丁香和兔心的治疗效果好。红花在咳嗽、痰白沫多方面治疗效果比丁香和兔心的治疗效果好。因此，对于胸刺痛、咳嗽和痰白沫多严重的患者可以使用表5中的药物配伍；对于心悸严重的患者可以使用表4中的药物配伍。
[0092]
综上可知，本发明的对病症症状进行药物匹配的方法是可靠的。
[0093]
以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。