适用于蜂窝型钢筒仓的结构体系的制作方法

本发明涉及工农业生产储存领域中钢筒仓结构设计技术领域，尤其涉及一种适用于蜂窝型钢筒仓的结构体系。

背景技术：

筒仓是工农业生产运输等过程中用来储存散装物料的仓库。近年来，随着行业的发展，人们对物料储存库，特别是对其容积的要求越来越高，有些钢筒仓的容积甚至达10万立方以上，这对大容积钢筒仓的设计提出新的挑战。目前实际工程中设计应用的筒仓基本上是圆形形状，这使得大容积筒仓的直径非常大，有时可达100多米。大容积圆形筒仓在实际工程中多设计为落地式平底仓，采用地道式出料方式，常在基础底板上按一定间距开设多个一定大小尺寸的卸料口，即形成所谓的“多点卸料”方式。对采用多点卸料方式的大容积筒仓，卸料时为了操作的便宜，底板卸料口开放的位置及个数往往是随机的，即实际工程中采用多点卸料方式时，保证筒仓的中心对称卸料往往是不现实的，因而偏心卸料甚至大偏心卸料就不可避免。卸料过程中的偏心引起钢筒仓仓壁散料压力在周向和竖向的不均匀分布，使结构的承载力显著降低。

技术实现要素：

本发明的目的是为了解决满足蜂窝形钢筒仓这一新型的空间结构的各项力学性能要求等问题，提出一种适用于蜂窝型钢筒仓的结构体系。

为了达到上述目的，本发明所采用的技术方案如下：一种适用于蜂窝型钢筒仓的结构体系，所述筒仓由若干单仓相连而成，所述筒仓的横截面为蜂窝形状，所述单仓的横截面为正六边形，所述单仓的一个面由若干仓壁平板、两个竖直框架角柱、若干竖直框架中间柱、若干水平框架梁构成，所述若干竖直框架中间柱分布在两个竖直框架角柱之间，所述竖直框架角柱和竖直框架中间柱之间以及相邻两个竖直框架中间柱之间通过水平框架梁垂直相交焊接，所述竖直框架角柱和竖直框架中间柱在焊接节点处竖向连续；所述水平框架梁在节点处，其横截面焊接在竖直框架角柱或竖直框架中间柱的侧面上；所述单仓一个面上的两个竖直框架角柱、若干竖直框架中间柱和若干水平框架梁连接构成框架；所述仓壁平板焊接在框架上，所述单仓的相连两个面采用公共的竖直框架角柱,所述单仓的六个面依次连续构成一个单仓；所述仓壁平板、竖直框架角柱、竖直框架中间柱以及水平框架梁构成框壳结构。

进一步的，所述仓壁平板位于框架的一侧，或仓壁平板位于框架的中面上。

进一步的，所述仓壁平板的厚度采用均匀壁厚或采用阶梯型变壁厚形式。

进一步的，所述竖直框架角柱和竖直框架中间柱的截面采用矩形钢管、方形钢管、槽钢或I字钢。

进一步的，还包括支架，所述筒仓支撑在支架上。

与现有技术相比，本发明的有益效果如下：

1)卸料偏心对蜂窝仓结构承载力的影响甚微，这是蜂窝仓显著优于传统圆形仓的特征之一。平面是由多个六边形单仓组合而成，每个六边形单仓仓底均布设有单独卸料口，因而每个单仓在装卸料时都是相对独立的。大直径圆形钢筒仓虽然也采用带仓底卸料口的多点卸料方式，但由于仓内流动通道不是独立的，而其实际为假想的流动通道，卸料时卸料口开放的个数和位置都是随机的，因而圆形落地仓卸料时各卸料通道相互干扰，其对仓壁的散料压力分布影响非常显著，使仓壁散料压力沿周向和竖向均显著不均匀分布。蜂窝形钢筒仓也可采用多点卸料方式，各单仓可同时或单独卸料，单仓间由于有共同仓壁阻隔，因而卸料时仓内流动通道之间互不影响或相互影响较小。当蜂窝形群仓中的某些偏离蜂窝仓形心的单仓卸料时，相对整体而言即是偏心卸料，偏心的程度由工作单仓与蜂窝形心的相对位置确定，因此偏心卸料甚至大偏心卸料对蜂窝形钢筒仓的影响是也是很小的。

2)蜂窝仓可以实现土地的高效利用。圆形筒仓群仓的平面布置多采用行列式的形式，各筒仓之间存在空隙，因而不利于节地。对于蜂窝形筒仓组合群仓而言，各单仓间不存在空隙，在群仓内部两相邻筒仓共享仓壁，各单仓之间通过仓壁相连，形成一个大型带隔板的多边形“筒仓群”。因而六边形筒仓组成的群仓有利于节地，特别是对土地资源紧张的情况下，采用蜂窝形筒仓群无疑是有利的。

3)蜂窝形钢筒仓施工方便，建造周期缩短。蜂窝形钢筒仓的各仓壁为平面形状，其曲率为零，与圆形钢筒仓的仓壁相比，施工建造时不需要弯曲加工，且平面形状的钢板焊接时也比弧形钢板的焊接更为方便，因而可以节约大量的加工时间；另外，蜂窝形钢筒仓仓壁钢板的厚度要远小于相同容积和高度的圆形钢筒仓，因而也可大大节约筒仓的加工制作时间且施工质量更易保证。

4)蜂窝仓可实现高效节约用材。蜂窝形群仓内部两相邻钢筒仓共享仓壁，因而可以节约一定材料，并缩短施工周期。随着蜂窝形钢筒仓中所组成的六边形单仓的个数的增大，这种优点更加突出。

附图说明

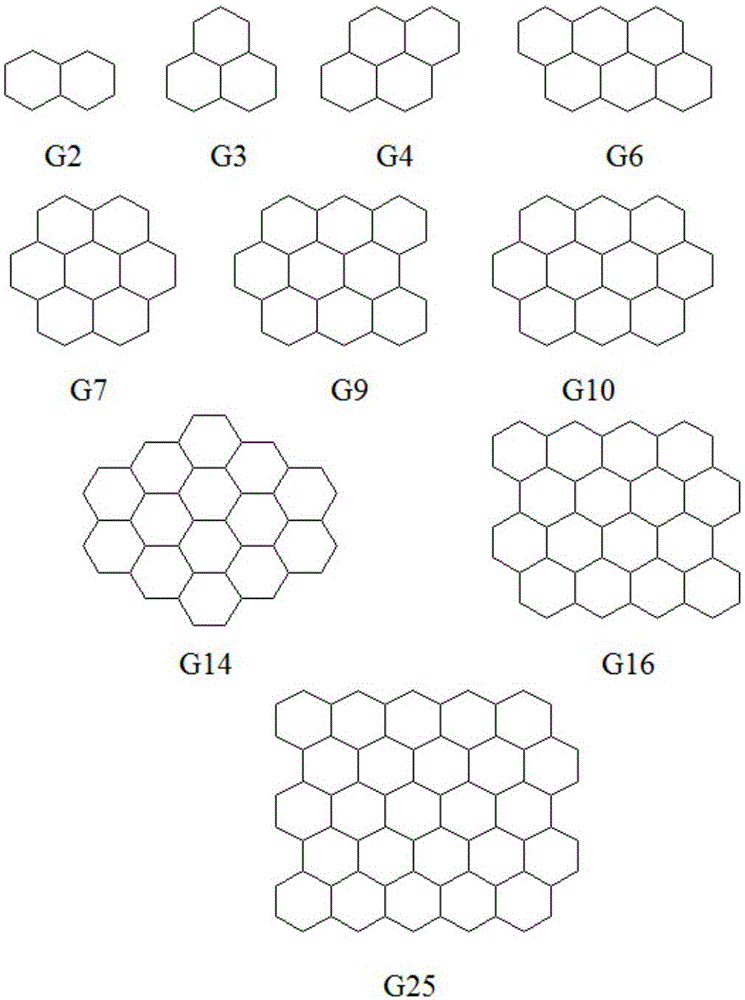
图1为不同个数六边形单仓组合群仓的平面布置图；

图2为六边形钢筒仓框壳结构布置图；

图3为算例蜂窝形筒仓平面布置示意图；

图4为六边形钢筒仓几何尺寸图；

图5为六边形钢筒仓整体有限元模型图；

图6为圆形钢筒仓屈曲模态图；

图7为六边形框壳结构加劲肋布置方案和构件截面布置图；

图8为六边形壳单元钢筒仓变形形状图；

图9为六边形钢筒仓框壳结构1屈曲模态图；

图10为六边形钢筒仓框壳结构2屈曲模态图；

图11为六边形钢筒仓框壳结构3屈曲模态图；

图12为六边形钢筒仓框架结构屈曲模态图；

图13为框壳结构钢筒仓非线性屈曲分析荷载-位移全过程曲线图；

图14为框壳结构3荷载-位移曲线的斜率随位移的变化过程图；

图15为两仓组合时分析工况图；

图16为两仓组合群仓LBA屈曲模态图；

图17为两仓组合群仓GNA屈曲模态图；

图18为两仓组合群仓GMNA屈曲模态图；

图19为三仓组合群仓分析工况图；

图20为三仓组合群仓LBA屈曲模态图；

图21为三仓组合群仓GMNA屈曲模态图；

图22为蜂窝形钢筒仓分析工况图；

图23为蜂窝形群仓LBA分析典型屈曲模态图；

图24为蜂窝形群仓GMNA分析典型屈曲模态图；

图中，仓壁平板1、竖直框架角柱2、竖直框架中间柱3、水平框架梁4、壳单元5、梁单元6。

具体实施方法

为使本发明的内容更加明显易懂，下面结合附图及具体实施方法进一步阐述。

图1为不同个数六边形单仓组合群仓的平面布置图，图2为六边形钢筒仓框壳结构布置图；为本发明提供一种适用于蜂窝型钢筒仓的结构体系，所述筒仓由若干单仓相连而成，所述筒仓的横截面为蜂窝形状，所述单仓的横截面为正六边形，所述单仓的一个面由若干仓壁平板1、两个竖直框架角柱2、若干竖直框架中间柱3、若干水平框架梁4构成，所述若干竖直框架中间柱3分布在两个竖直框架角柱2之间，所述竖直框架角柱2和竖直框架中间柱3之间以及相邻两个竖直框架中间柱3之间通过水平框架梁4垂直相交焊接，所述竖直框架角柱2和竖直框架中间柱3在焊接节点处竖向连续；所述水平框架梁4在节点处，其横截面焊接在竖直框架角柱2或竖直框架中间柱3的侧面上；所述单仓一个面上的两个竖直框架角柱2、若干竖直框架中间柱3和若干水平框架梁4连接构成框架；所述仓壁平板1焊接在框架上，所述单仓的相连两个面采用公共的竖直框架角柱2,所述单仓的六个面依次连续构成一个单仓；所述仓壁平板1、竖直框架角柱2、竖直框架中间柱3以及水平框架梁4构成框壳结构。

进一步的，所述仓壁平板1焊接在框架上有两种方式：所述仓壁平板1位于框架的一侧，或仓壁平板1位于框架的中面上。

进一步的，所述仓壁平板1的厚度采用均匀壁厚或采用阶梯型变壁厚形式。

进一步的，所述竖直框架角柱2和竖直框架中间柱3的截面采用矩形钢管、方形钢管、槽钢或I字钢。

进一步的，还包括支架，所述筒仓支撑在支架上。

下面通过实施例对本发明作进一步的说明。

实施案例：

1、工程案例

以实际工程中的某蜂窝形筒仓为例，如图3所示为工程的平面布置示意图。蜂窝仓结构总长度为210.35m，总宽度为60.45m，呈四行布置，共有48个六边形，每16个六边形为一组(图1的G16)，共3组，每组群仓间的净距离为3.0m，六边形单仓边长l_c＝9.3m，仓筒的有效高度h_c＝23.55m，如图4所示，根据六边形的内切圆可计算六边形钢筒仓的有效直径可得六边形钢筒仓单仓长细比h_c/d_c＝1.462，属欧洲规范中深仓和我国规范浅仓的范畴。为便于比较，表中还列出了相同直径d_c和高度h_c的圆形钢筒仓。两种平面形状的钢筒仓几何参数详见表1.1，表中仓壁厚度经多次试算确定，并假设为阶梯形分布。

表1.1钢筒仓设计技术参数一览表

该工程为发电厂，筒仓中的散料为煤炭，分析采用欧洲设计规范系列，参考欧洲规范的设计条件，假设仓壁表面等级为D1，作用评估等级为AAC2，各钢筒仓分析时所采用的物理力学参数可确定如下表1.2所列。

表1.2散料物理力学参数一览(物料：煤炭)

对六边形钢筒仓而言，由于其仓壁为平面，仓壁不仅作用有散料产生的平面内竖向摩擦力还作用有平面外水平压力。由平板的结构特性可知，仓壁的平面外刚度较小，为提高仓壁的平面外刚度，需要设置水平向和竖向加劲肋以抵抗仓壁表面的散料水平压力。此外，六边形钢筒仓和圆形钢筒仓的有限元模型也存在较大差异，分析中假设六边形单仓的仓底为固支，为分析方便，在六边形钢筒仓有限元模型中不包含仓顶屋面等结构，但模型中包括抗风环梁及各种水平和竖向加劲肋。采用大型商业有限元软件ANSYS进行分析，根据六边形平面形状及荷载分布特点，数值分析采用整体有限元模型，如图5所示，结构中的仓壁采用壳单元SHELL93模拟，而各种加劲肋(包括风梁)则采用梁单元BEAM189模拟。在数值分析计算中，通过弧长法(arc length method)来跟踪非线性稳定分析的荷载-位移全过程曲线。

2、六边形单仓结构选型及稳定性能

2.1等长细比圆形钢筒仓分析

为便于比较，本工程实例同时给出相同长细比的圆形钢筒仓有限元分析结果，圆形钢筒仓分析采用的几何参数见表1.1所示，壁厚采用阶梯型分布形式，仓壁沿竖向共分为8段，分段的高度自上而下分别为2.55、3.0、3.0、3.0、3.0、3.0、3.0、3.0m，对应壁厚分别为4.0、4.0、5.0、5.0、6.0、6.0、7.0、8.0mm，等效厚度为5.66mm，圆形钢筒仓仓壁未设置加劲肋。根据钢筒仓结构在轴对称散料荷载作用下的变形云图，可知结构的变形也是轴对称的，最大径向位移发生在仓壁底部，约为3.8mm，远小于规范规定的位移限值。圆形钢筒仓在稳定分析GMNA下的屈曲模态如图6所示，仓壁发生弹塑性变形，仓底为典型的“象脚破坏”模式，临界屈曲荷载系数λ_cr约为1.78，考虑焊接初始几何缺陷的影响后，其临界屈曲荷载系数λ_cr约为1.68，满足欧洲规范对稳定承载力的要求。

2.2单仓的结构选型及稳定性能

圆形钢筒仓是典型的薄壳结构，壳单元是结构的主要受力部分，而加劲肋(如果设置)则是一种提高结构稳定性能的措施。而对六边形钢筒仓，由于结构不再是轴对称的，先前针对圆形钢筒仓的研究成果将可能不再适用，本工程实例主要针对六边形钢筒仓采用多种模型进行结构选型，力求寻找针对六边形钢筒仓稳定承载能力最优的结构形式。根据六边形钢筒仓的平面形状以及仓壁表面散料压力的分布形式，对拟分析的六边形钢筒仓可能采用的结构形式有：

薄壳结构：与圆形钢筒仓相同，结构的有限元模型中仅包含壳体单元，结构的承载能力由组成仓壁的薄壳单元承担。

框架-薄壳结构：这种结构形式的有限元模型中不仅包括壳体单元还包括各种梁单元，结构的承载能力由组成仓壁的薄壳单元和组成各种加劲肋的梁单元共同承担，两种单元协调变形、协调受力，组成新的结构形式，也简称为框壳结构。本工程实例对框壳结构采用三种不同的框架梁柱布置和截面分布形式(图7)进行分析。

框架结构：这种结构形式的有限元模型中仅包含梁单元，结构的承载能力由组成加劲肋的梁单元承担。

本工程实例对以上三种可能的结构形式进行线性静力(LA)和屈曲分析。屈曲分析的类型仅考虑几何完善模型，即主要考虑以下3种类型的屈曲分析：

1)LA-线弹性静力分析；

2)LBA-几何完善钢筒仓的线性分支屈曲分析；

3)GNA-几何完善钢筒仓的几何非线性、弹性静力屈曲分析；

4)GMNA-几何完善钢筒仓的几何非线性、弹塑性静力屈曲分析。

2.2.1六边形钢筒仓-薄壳结构

六边形钢筒仓采用壳体结构，单仓的几何尺寸见表1.1及图4，仓壁分段数及各分段厚度同上节圆形钢筒仓，六边形单仓在线弹性分析(LA)下的变形形状如图8所示，变形受仓底和仓顶边界条件的影响非常明显，主要是各仓壁的外鼓变形，最大变形约发生在仓壁的中上部，最大侧向位移约为357.6m，为相同长细比圆形钢筒仓最大径向位移的9万多倍；仓壁水平向应力不但沿竖向分布不均匀，而且在同一高度处沿水平向分布也是不均匀的，仓壁水平应力的最大值约在高度的2/3处，发生在两条仓壁交界的边界处，在仓壁中部最小，最大值与最小值的比值约为2.5；六边形钢筒仓结构抵抗散料压力的侧向刚度远远小于圆形钢筒仓的侧向刚度，由于六边形钢筒仓存在着棱角边界，引起了应力分布的显著不均匀和应力集中，这些特性必然会显著降低六边形钢筒仓结构的稳定承载能力。这也从另一角度说明，对圆形钢筒仓结构有利的水平内压，在六边形钢筒仓中成为最不利的控制荷载，该六边形薄壳钢筒仓结构在散料荷载作用下的GMNA屈曲临界荷载系数仅为0.19。

由以上分析可知，当圆形钢筒仓和六边形钢筒仓采用薄壳结构且采用相同的壁厚分布时，六边形钢筒仓的侧向刚度及稳定承载能力显著降低，水平内压成为控制六边形钢筒仓稳定设计的最不利荷载之一，对本算例而言，在GMNA分析下，六边形单仓的临界屈曲荷载系数仅为圆形钢筒仓的临界屈曲荷载系数的1/9.5，因而薄壳结构并不适用于六边形钢筒仓。

2.2.2六边形钢筒仓-框壳结构

上述六边形钢筒仓采用壳体结构的刚度及稳定承载力很低，自然可以想到，在仓壁设置加劲肋可以提高钢筒仓结构的侧向刚度及稳定性能。需要说明的是圆形钢筒仓中加劲肋的作用主要是提高仓壁的稳定承载力，仓壁壳单元是主要的受力构件，加劲肋是次要的结构构件，是一种构造措施。

现介绍带加劲肋六边形钢筒仓与带加劲肋圆形钢筒仓有着本质的区别，带加劲肋的圆形钢筒仓中，仓壁壳单元为主要受力构件，而加劲肋仅是为了提高结构的整体或局部稳定承载力而设置的附加措施，因而本质上仍是薄壳结构。带加劲肋六边形钢筒仓结构为薄壳单元和框架梁单元(加劲肋)共同抵抗散料荷载，框架和与框架相连的薄壳单元共同工作协调变形，因而是一种新颖的结构类型，本发明称为框架-薄壳结构或简称框壳结构。在框壳结构中，壳体单元的受力更加复杂，一方面它承受散料荷载的直接作用，并把散料荷载传递给相邻的框架结构单元，另一方面，壳体单元与框架梁单元共同受力，可以显著提高框架结构的整体刚度，特别是抗扭刚度，因而是一种新颖的组合结构。

在六边形钢筒仓框壳结构中，同样假设仓壁分段的高度不超过3.0m，这样仓壁沿竖向共分为8段，每段仓壁的交界处设置水平加劲肋共8条，如图7中（a）所示。竖向加劲肋的布置方式假设为如下三种形式：框壳结构1仅在六边形仓壁的交界处(棱角处)设置竖向加劲肋，因而共设置6根竖向加劲肋；框壳结构2除在六边形仓壁的交界处设置竖向加劲肋以外，同时还在各边的中间位置也设置竖向加劲肋，因而共设置12根竖向加劲肋；框壳结构3除在六边形仓壁的交界处设置竖向加劲肋外，同时还在各边的1/3分段位置也设置竖向加劲肋，因而共设置18根竖向加劲肋，加劲肋的截面布置详见图7中(b)所示。三种框壳结构中水平加劲肋的布置是相同的，框壳结构1中竖向加劲肋的间距为9.3m，框壳结构2中竖向加劲肋的间距为4.65m，框壳结构3中竖向加劲肋的间距为3.1m。在数值分析中横向及纵向加劲肋采用BEAM189单元离散，仓壁采用SHELL93离散。由于在框壳结构中，水平和竖向加劲肋构成框架，为便于表达，下文中水平加劲肋称为框架梁，竖向加劲肋称为框架柱。

框壳结构1中的梁柱布置及截面分布见图7中（a）和7中（b）所示，框架梁柱均采用方形钢管截面BOX。经线性分析(LA)，框壳结构1中仓壁的最大侧向位移约为0.385m，发生在仓壁的中下部；钢筒仓在屈曲分析LBA、GNA、GMNA下的屈曲模态见图9所示，其中线性分支屈曲LBA的第一阶屈曲模态为仓壁的反对称局部屈曲，主要发生在仓壁下部区域；GNA考虑了几何非线性，GMNA同时考虑几何非线性和材料非线性，两者的屈曲模态基本类似，结构的变形主要是仓壁的整体弯曲变形，散料的水平压力使原六边形仓壁发生圆筒化变形的趋势，其中仓壁中上部变形最大，最大平面外位移发生在仓壁顶部中间部位节点，而仓壁下部由于受边界约束的影响，有保持原来六边形形状的趋势。

框壳结构1在屈曲分析LBA、GNA、GMNA下的临界屈曲荷载系数见表1.3所示，由表可见，由于线性分支屈曲为仓壁壳体单元的局部屈曲，结构的整体承载能力没有发挥，因而其临界屈曲荷载系数很小，它不是结构发生屈曲的真实变形形状，另外，由于线性屈曲发生在底部部位，主要是仓壁局部屈曲引起，因而总可以通过优化该部分仓壁厚度而提高结构的稳定承载力。同时GNA分析结果表明，考虑几何非线性时，结构的临界屈曲荷载系数有很大提高，GNA分析时的临界屈曲荷载系数相对于LBA分析时，提高了约12多倍。考虑几何非线性及材料非线性的GMNA分析表明，材料非线性对结构的临界屈曲荷载是非常不利的，它使结构的临界屈曲荷载系数显著降低，对框壳结构1，GMNA分析时的临界屈曲荷载系数仅为GNA分析时临界屈曲荷载系数的0.31倍，即材料非线性的不利作用使结构的屈曲临界荷载系数降低约69％。框壳结构1在GMNA分析下的临界屈曲荷载系数仅为0.55，远小于规范对稳定设计整体安全系数的要求。表明仓壁的侧向刚度较小，需要对仓壁进行加强设计。

表1.3框壳结构屈曲临界荷载系数λ_cr

2.2.3六边形钢筒仓-框壳结构

框壳结构2中的框架梁柱布置及截面分布分别见图7中（a）和（b）所示，框架梁柱也采用方形钢管截面BOX，在线性分析中仓壁的最大侧向位移约为0.320m，发生在仓壁的中下部；钢筒仓在屈曲分析LBA、GNA、GMNA下的屈曲模态见图10所示，其中线性分支屈曲LBA的第一阶屈曲模态也为仓壁的反对称局部屈曲，主要发生在仓壁下部区域，与框壳结构1相比，由于跨中竖向加劲肋的影响，仓壁在水平方向的屈曲更加局部化，在周向引起了两个变形的局部区域；非线性屈曲分析GNA、GMNA的屈曲模态与框壳结构1类似，均使结构发生圆筒形状变化的趋势。框壳结构2在屈曲分析LBA、GNA、GMNA下的临界屈曲荷载系数见表1.3所示，结果也表明，几何非线性对结构的临界屈曲荷载是有利的，而材料非线性则是显著不利的。

另外，框壳结构2在GMNA分析下的临界屈曲荷载系数增大为0.93，与框壳结构1相比，屈曲临界荷载系数约提高70％，表明跨中竖向加劲肋的作用非常明显，主要原因在于：框壳结构1中的水平加劲肋的跨度为六边形钢筒仓仓壁的边长，即为9.3m，而在框壳结构2中由于跨中竖向加劲肋的设置，水平加劲肋的跨度为六边形钢筒仓仓壁边长的一半，即为4.65m，跨度大大减少，而仓壁的侧向刚度主要受水平加劲肋的影响较大，水平加劲肋的跨度减小，其侧向刚度必显著增强，表现为屈曲特性上即是结构的临界屈曲荷载系数显著提高。框壳结构2在GMNA分析下的临界屈曲荷载系数仍小于规范对稳定设计整体安全系数的要求，表明结构的侧向刚度仍需要进一步提高。

2.2.4六边形钢筒仓-框壳结构

框壳结构3中的框架梁柱布置及截面分布分别见图7中（a）和（b）所示，梁柱也采用方形钢管截面BOX，在线性分析中仓壁最大侧向位移约为0.280m，发生在仓壁的中下部；钢筒仓在屈曲分析LBA、GNA、GMNA下的屈曲模态见图11所示，其中线性分支屈曲LBA的第一阶屈曲模态也为仓壁壳单元的反对称局部变形，主要发生在仓壁下部区域，与框壳结构1和2相比，由于水平加劲肋跨度的进一步减小，仓壁在水平方向的屈曲更加局部化，屈曲仅在仓壁跨度的中跨发生了局部变形，两边跨则未发生变形；非线性屈曲分析GNA、GMNA的屈曲模态与框壳结构2类似，均为仓壁的整体弯曲变形。框壳结构3在屈曲分析LBA、GNA、GMNA下的临界屈曲荷载系数见表1.3所示，结果也表明，几何非线性对结构的临界屈曲荷载也是有利的，而材料非线性则使结构的屈曲临界荷载系数显著降低。

另外，框壳结构3在GMNA分析下的临界屈曲荷载系数增大为1.66，稍大于规范对稳定设计整体安全系数的要求；与框壳结构2相比，框壳结构3中水平加劲肋的跨度由4.65m减小为3.10m，其侧向刚度增强，结构的临界屈曲荷载系数约提高78％。可以证明，当在仓壁中间设置3道或以上竖向加劲肋时，即仓壁水平加劲肋的跨度进一步减小，随着仓壁的侧向刚度增强，结构的屈曲临界荷载系数会进一步提高。但考虑实际工程施工及设计等条件，本申请采用水平加劲肋跨度为3.1m时的框壳结构3，可满足规范对钢筒仓结构稳定设计整体安全系数的要求。

2.2.5六边形钢筒仓-框架结构

上述三种六边形钢筒仓采用框壳结构，在这种结构体系中，仓壁壳单元和框架梁单元协调工作，共同提供抵抗散料荷载的平面外和平面内刚度。为了说明仓壁壳单元和框架梁单元均是不可或缺的，假设框架梁柱的布置及截面同框壳结构3中的框架结构，如图7。分析中仅考虑框架梁柱的刚度，而忽略仓壁壳单元的刚度，即对六边形钢筒仓采用框架结构进行分析。六边形钢筒仓框架结构在GMNA屈曲分析下的屈曲临界荷载系数仅为0.52，对应的屈曲模态如图12所示。结果表明，由于计算中忽略了仓壁壳单元的作用，结构的整体刚度显著降低，六边形钢筒仓框架结构的屈曲模态为稳定承载力很低的整体扭转变形；尽管六边形仓壁壳单元对结构稳定承载力的贡献比圆形钢筒仓中仓壁壳单元对结构稳定承载力的贡献相对小得多，但在六边形钢筒仓中，仓壁壳单元是结构组成中不可或缺的一部分，它对保证仓壁和框架加劲肋协同工作共同抵抗外荷载至关重要，因而在实际分析中应充分考虑六边形钢筒仓中仓壁壳单元和框架梁单元的共同作用，采用框壳结构体系。

2.2.6框壳结构钢筒仓荷载-位移全过程特点

结构的屈曲特性总是和其荷载-位移全过程响应密切相关的，上述三类框壳结构在散料荷载作用下的荷载-位移曲线如图13所示(GMNA分析结果)，其中监控位移点取自仓壁最大侧向挠度对应的节点。由图可见，三类框壳结构的荷载-位移曲线都是高度非线性的，框壳结构1的屈曲临界荷载系数λ_cr很小，仅为0.55，主要是由于仓壁框架梁跨度较大而侧向刚度较弱引起；由于在仓壁中部设置了竖向加劲肋，框壳结构2中的水平连系梁跨度减小为4.65m，因而侧向刚度显著提高，屈曲临界荷载系数λ_cr增大到0.93，与框壳结构1相比，λ_cr约提高了0.7倍。当在仓壁继续增加竖向加劲肋而使水平框架梁进一步减小后，仓壁侧向刚度仍会继续增大，表现为结构的屈曲临界荷载系数进一步提高。如框壳结构3在仓壁中部设置了两道竖向加劲肋，水平连系梁的跨度减小为3.1m，结构的屈曲临界荷载系数λ_cr增大到1.66，与框壳结构2相比，λ_cr约提高78％。这个屈曲临界荷载系数能满足规范对结构整体稳定的要求。

框壳结构荷载-位移全过程响应反映了结构屈曲的过程特点，结构的荷载-位移全过程曲线及曲线的斜率都反映了变形过程中结构刚度的相对变化，如图14所示为曲线斜率随结构变形的变化过程，以框壳结构3为例，结构屈曲的全过程可分为如下三个典型的阶段：

1)线性阶段：在结构承受荷载的初始阶段，结构的位移响应与散料荷载基本呈线性关系，在图13上表现为一段水平直线，即该段曲线的斜率为常数，但相对结构的全过程，线性阶段的范围较小，线性段荷载系数最高点对应的相应位移w₀约为3.5t_m，其中t_m为六边形仓壁的平均厚度，对应的荷载系数仅约为0.15。仓壁壳单元由于弯曲变形较小，平面外刚度也较小，这一阶段的结构侧向刚度主要由框架单元提供。在该范围内结构的变形也基本处于弹性范围，仓壁最大Mise应力约为300MPa，发生在两条仓壁交汇处的中部位置，仓壁应力沿水平和竖向的分布都是不均匀的。

2)强化阶段：当结构荷载超过线性阶段的最大荷载时，结构的荷载-位移曲线表现为显著的非线性特性。相对结构的全过程，强化阶段的范围很大，其荷载系数最高点对应的最大位移w_max约为110.0t_m，对应的荷载系数约为1.66。强化阶段又可以细分为两个子阶段：前强化阶段和后强化阶段，该阶段荷载位移曲线的斜率均为正值，如图14。

前强化阶段在荷载-位移曲线上的主要特征是结构位移显著增加而相应的荷载增量越来越小，曲线在图形上为上凸，即曲线的二阶导数为负值，表现为曲线的斜率逐渐变小，但斜率仍为正值，如图14所示，结构的侧向刚度有减小的趋势。这一阶段的结构侧向刚度主要由框架结构承担，而仓壁壳单元发生了一定的弯曲变形，薄膜效应逐渐对结构产生影响，可对结构提供一部分侧向刚度，这一特征以侧向位移w₁约为40.0t_m时为转折点，对应的荷载系数约为0.4。

当荷载继续增加后，结构进入后强化阶段，这一阶段在荷载-位移曲线上的主要特征是结构荷载增量显著增加而相应的位移增量越来越小，曲线在图形上为下凸，即曲线的二阶导数为正值，表现为曲线的斜率逐渐变大，结构的侧向刚度随位移增加而增大，如图14所示。这一阶段中仓壁壳单元发生了很大的弯曲变形，薄膜效应十分显著，且随着仓壁弯曲变形的增大，薄膜效应对结构刚度的贡献也逐渐增大，这一阶段结构的侧向刚度主要由仓壁薄壳单元和框架梁单元共同提供，特别是在这一阶段的末尾，荷载-位移曲线的斜率急剧增大，在最大侧向位移w_max约为110.0t_m时，结构的荷载系数取得最大，约为1.66。

3)衰减阶段：在强化阶段的末尾，结构的荷载系数取得最大值，而后结构的刚度突然变小并在位移基本无变化的情况下，荷载系数急剧减小至零。表明在这一阶段，结构丧失了承受荷载的能力。

上述六边形框壳结构钢筒仓在散料荷载作用下的屈曲过程曲线与圆形钢筒仓在散料荷载作用下的荷载-位移全过程曲线有着明显的区别，主要表现在：

1)圆形钢筒仓的荷载位移曲线是典型薄壳结构的屈曲行为。六边形钢筒仓的屈曲主要是由平面仓壁屈曲引起的，图13所示的结构荷载-位移屈曲过程，实际上与带加劲肋平板结构的弯曲屈曲过程相类似。六边形钢筒仓框壳结构的屈曲本质上属于平板结构的屈曲行为。

2)六边形框壳结构钢筒仓屈曲延性要显著优于圆形钢筒仓。以往研究表明，与六边形钢筒仓长细比接近的圆形钢筒仓的屈曲临界位移约为1.83t_m，而六边形框壳结构钢筒仓屈曲时的最大侧向位移w_max可达约110.0t_m，因而结构延性显著优于圆形钢筒仓。

3组合群仓结构的稳定性能

根据上述对六边形单仓在散料荷载作用下的稳定性能的分析，指出了圆形钢筒仓的结构稳定性能要显著优于相同长细比的六边形单仓，而两种平面形状的钢筒仓的结构体系也发生了显著变化，即圆形钢筒仓的受力体系主要是薄壳结构，而六边形钢筒仓的受力体系主要是框壳结构。然而，研究六边形单仓的意义显然不仅于此，由于六边形单仓在平面组合上的便宜性和优越性，理论上六边形单仓在平面上可以通过任意数目的组合而生成设计形状的群仓，常见的组合群仓如图1-2所示。下面介绍一下单仓个数为两个(G2)、三个(G3)等基本组合数时，各组合群仓在散料荷载作用下的稳定性能，继而归纳出蜂窝形组合群仓的一些结构特点。

3.1两仓组合群仓

六边形单仓是集束式蜂窝形钢筒仓组成的基本单元，而两仓组合群仓是最简单的组合群仓，也是群仓结构分析的一个重要组成部分，根据群仓中各单仓装卸料的相对关系，两仓组合群仓主要有以下两种分析工况，如图15所示。为便于描述，现把群仓中的单个六边形仓称为基仓，以区别于上述的单仓。

3.1.1分析工况

当群仓中的一个基仓装卸料，而另一基仓为空仓时，显然这种情况下由于空仓的支撑作用，工作基仓的受力性能要明显优于单仓，如图15所示的工况1；当群仓中的两个基仓同时装卸料时，显然两基仓相邻公共仓壁两侧的散料竖向摩擦力相互叠加，因而要远大于单仓的单侧竖向摩擦力，而公共仓壁两侧的散料水平压力由于作用方向相反，当两基仓同时装卸料时而基本相互抵消，如图15所示的工况2。这样群仓的公共仓壁仅作用有叠加的散料竖向摩擦力而不存在水平散料压力，而边界仓壁则同单仓时相同，仓壁上同时存在散料竖向摩擦力和水平向压力。

由于群仓仓壁上散料荷载分布的这些显著特点，公共仓壁上的钢板厚度和框架梁柱截面与其它边界仓壁存在一定差别，在分析过程中对公共仓壁壁厚和框架梁柱截面作相应优化。

3.1.2稳定性能

两仓组合群仓结构的LBA线性屈曲模态如图16所示，由图可见，工况1和工况2时的结构屈曲变形都是高度局部化的，与单仓的屈曲模态类似，变形仅发生在结构底部的仓壁壳单元部位，且框架梁柱单元基本没有变形；对工况1，局部变形主要发生在工作基仓，而相连的空仓则没有发生变形，对工况2，局部变形也发生在两个工作基仓的底部。对局部变形外的其它区域则基本保持结构的原有形状。

两仓组合群仓结构在GNA和GMNA分析下的屈曲模态也与单仓相应的屈曲模态类似，如图17和图18所示，结构的变形主要表现为仓壁的整体弯曲屈曲，仓壁壳体单元和框架梁柱共同变形。对工况1而言，荷载作用的基仓对临近空仓的变形有一定影响，使与之相连的空仓仓壁产生附加变形，反过来，空仓也对临近基仓产生一定支撑作用，表现在变形上则是两基仓的公共仓壁的平面外侧移显著小于荷载作用工作基仓的其它各仓壁的平面外侧移；对工况2，两相邻基仓均有散料荷载作用，因而互为支撑，且互相分担相互传来的部分荷载，作用的结果表现在屈曲模态上则是两基仓共同发生整体弯曲变形，相邻公共仓壁由于两侧水平向左右荷载的方向相反，因而其平面外变形很小。

另外，群仓结构在各工况下非线性GMNA分析的荷载-位移全过程基本与图13类似，但两仓组合群仓模型显得更加复杂，与单仓结构相比，其曲线在第二阶段的荷载-位移响应的斜率变小，结构的基本特性没有发生变化。

两仓组合群仓结构在各荷载工况下的线性和非线性屈曲临界荷载系数见表1.4所示，线性屈曲LBA分析的临界屈曲荷载系数均小于非线性屈曲分析，主要原因在于两者屈曲模态的显著差异，在线性屈曲中，结构的屈曲模态为仓壁的局部屈曲，结构承载力没有充分发挥，表现为临界屈曲荷载系数很小。非线性屈曲分析表明，几何非线性对结构的稳定承载力是有利的，与线性屈曲相比临界屈曲荷载系数约提高15～20倍；而GMNA分析时的材料非线性对结构的稳定承载力是不利的，与GNA分析相比，临界屈曲荷载系数约降低了约60％～78％，由于对这种结构分析中总是存在大变形效应并伴随着仓壁材料的弹塑性屈服，因而结构的稳定承载力应通过GMNA分析来考察(假设不考虑初始几何缺陷)，按欧洲设计规范的要求承载力荷载系数不小于1.65。另外，两仓组合结构在工况1、工况2时的临界屈曲荷载系数也存在显著差别，对工况1，由于空仓对荷载作用的基仓起一定的支撑作用，因而结构在工况1时的GMNA屈曲临界荷载系数比上节研究的单仓要高很多，同时也比工况2时的屈曲临界荷载系数大很多，其临界荷载屈曲系数约为工况2时的屈曲临界荷载系数的2倍，这也说明对两仓组合群仓而言的最不利荷载工况为工况2，即两仓均为满仓。另外，与单仓结构相比，两仓组合群仓结构体系也为框壳结构，结构仓壁厚度与梁柱构件的截面及尺寸基本相同，仅在公共仓壁部位进行了优化。

表1.4两仓组合群仓结构的临界屈曲荷载系数λ_cr

3.2三仓组合群仓

三仓组合时，根据群仓中各基仓装卸料的相对位置关系，主要有以下三种分析工况，如图19所示。

3.2.1分析工况

当群仓中的一个基仓装卸料，而另两基仓为空仓时，显然这种情况下由于空仓的支撑作用，工作基仓的受力性能要明显优于单仓，由于三个基仓是关于公共角点中心对称的，因而三仓的位置是等价的，这种情况只有一个工况，如图19所示的工况1；当群仓中的两个基仓同时装卸料时，显然在两基仓相邻的公共仓壁的散料竖向摩擦力要远大于单仓，而公共仓壁的散料水平压力则由于两侧基仓散料的共同作用而基本抵消，由于三个基仓的位置是等价的，这种情况也只有一个工况，如图19所示的工况2。当三个基仓同时装卸料时，此为满仓工况，如图19所示的工况3。

3.2.2稳定性能

三仓组合群仓结构的线性屈曲模态如图20所示，由图可见，工况1～工况3时的结构屈曲变形都是高度局部化的，变形仅发生在结构底部的仓壁部位，且框架梁柱单元基本没有变形；对工况1，局部变形主要发生在工作基仓，而相连的两个空仓则没有变形；对工况2，局部变形发生在两个工作的基仓底部，而另一空仓则没有变形；对工况3，局部变形同时发生在三个工作基仓的底部。局部变形区域外的部位则基本保持原有形状。这也说明了线性屈曲时仓壁壳单元和框架梁柱单元的刚度没有充分发挥，而使其临界荷载系数显著偏小。

三仓组合群仓结构在GMNA分析下的屈曲模态如图21所示，结构的主要变形为仓壁壳体和框架共同发生的整体弯曲变形。对工况1而言，荷载作用的基仓对临近两个空仓的变形有一定影响，使相连的空仓仓壁产生附加变形，空仓也对临近基仓产生一定支撑，表现在变形上则是三基仓的公共仓壁的平面外侧移显著小于荷载作用基仓的其它各边平面外侧移；对工况2，两相邻基仓均有散料荷载作用，因而互为支撑，且互相分担相互传来的部分荷载，临近空仓对两工作基仓也起一定的支撑作用，作用的结果表现在屈曲模态上则是两工作基仓共同发生整体弯曲变形，相邻公共仓壁由于两侧水平向荷载的方向相反，因而其平面外变形很小，而空仓也只在与工作基仓相连的临近仓壁发生变形；满仓工况3的屈曲模态表现为三个工作基仓共同发生弯曲变形，而三仓的三个公共仓壁由于两侧散料的水平压力基本相互抵消，因而其平面外侧移很小。结构在几何非线性GNA分析下的屈曲模态基本与图21所示的变形形状类似，此不赘述。另外，群仓结构在各工况下非线性GMNA分析的荷载-位移全过程基本与图13类似，但三仓组合时的分析模型显得更加复杂，与单仓结构和两仓组合结构相比，其曲线在第二阶段的荷载-位移响应的斜率变的更小，甚至难以追踪，而结构的基本屈曲特性没有发生根本变化，仍属于带肋平板屈曲的范畴。

三仓组合群仓结构在各荷载工况下的线性和非线性屈曲临界荷载系数见表1.5所示，由表可见，线性屈曲LBA分析的临界屈曲荷载系数均小于非线性屈曲分析，主要原因在于两者屈曲模态的显著差异，在线性屈曲中，结构的屈曲模态为仓壁的局部屈曲，而群仓结构主要靠框架梁单元和仓壁壳体单元共同承受荷载的，因而结构的稳定承载力没有充分发挥，表现为临界屈曲荷载系数很小。非线性屈曲分析表明，几何非线性对结构的稳定承载力是有利的，与线性屈曲相比临界屈曲荷载系数约提高13～15倍；而GMNA分析时的材料非线性对结构的稳定承载力是不利的，与GNA分析相比，临界屈曲荷载系数约降低了约59％～73％，由于对这种结构分析中总是存在大变形效应并伴随着材料的弹塑性屈服，因而结构的稳定承载力应通过GMNA分析来考察，按欧洲设计规范的要求承载力荷载系数不小于1.65。另外，三仓组合结构在工况1、工况2、工况3时的临界屈曲荷载系数也存在显著差别，对工况1，由于两空仓对荷载作用的基仓起一定的支撑作用，因而结构在工况1时的GMNA屈曲临界荷载系数比上节研究的单仓要高很多且也比两仓组合工况1时的屈曲临界荷载系数略高；对工况2，临近空仓对两工作基仓也有一定的支撑作用，但与工况1相比，空仓的有利作用要小很多，因而工况2时的屈曲临界荷载系数比工况1约小31％；对工况3而言，在GMNA下的临界荷载屈曲系数最小，其值约为工况2时的68％，且与工况1时的屈曲临界荷载系数相比约减小52％，亦即三仓组合群仓时的最不利荷载工况为工况3，即三基仓均为满仓。另外，与单仓结构和两仓组合结构相比，三仓组合群仓结构体系也为框壳结构，结构构件的截面及尺寸基本相同，也仅在公共仓壁部位进行了局部优化。

表1.5三仓组合群仓结构的临界屈曲荷载系数λ_cr

4蜂窝形钢筒仓稳定分析

上面描述了两仓和三仓组合群仓结构在各种散料荷载工况下的稳定性能。在蜂窝形钢筒仓中，其组成基仓的个数较多，因而蜂窝形钢筒仓除具有上述单仓、多仓组合群仓的一些结构特征外，还可能具有其它一些显著的特点。现重点讨论蜂窝形钢筒仓的分析工况及各分析工况下的稳定性能。

4.1蜂窝形钢筒仓稳定分析荷载工况

本实例蜂窝形筒仓拟采用钢结构设计，平面布置如图3所示，蜂窝形筒仓中单仓的几何尺寸见表1.1和图4。由于蜂窝仓中3组群仓是相互独立的(每组群仓间净距离为3.5m)，因而可取任一组进行分析，即分析对象为G16组合群仓。若按群仓中各基仓装卸料的个数和各基仓相对位置关系，其分析工况将达上百种，若对每种分析工况均详加研究，其分析代价将是十分高昂的，再加上数值模型的复杂化，使得计算分析更加困难。组合群仓的稳定性能是由某些特定工况控制的，从而对有些工况的分析则是不必要的。由于最终各单仓可采用相同设计，故只需考察群仓中的单仓设计。总的来说，对这些工况进行归纳后，蜂窝形钢筒仓的分析工况可分为如下三种典型类别。本实例选择其中几种典型的工况进行分析，如图22所示。各组分析工况主要包含以下含义：

1)工况1～工况6，为一个基仓装卸料，而其余15个基仓为空仓，它表示单个基仓装卸料时，其余各空仓对单个工作基仓的支撑作用。这些工况相应于蜂窝仓在卸料末尾阶段的受荷状态。

2)工况7～工况12，为一个基仓为空仓，而其余15个基仓同时装卸料，它表示单个基仓空仓时，其余各工作基仓对单个空仓的影响。这些工况相应于蜂窝仓在卸料中间阶段的受荷状态。

3)工况13，该工况表示16个基仓同时装卸料时的情况，它代表满仓工况。该工况相应于蜂窝仓在卸料开始时的受荷状态。

4.2蜂窝形钢筒仓的稳定性能

4.2.1屈曲模态

蜂窝形群仓结构的线性屈曲模态如图23所示，各分析工况下的结构屈曲变形都是高度局部化的，变形仅发生在结构底部的仓壁部位，且主要发生在工作基仓的底部，群仓中的框架梁单元基本没有发生变形；由于各工况下的屈曲模态基本相似，图中仅给出了有代表性工况1、工况5、工况10、工况13时的屈曲模态。另外，除与工作基仓相连的空仓仓壁发生一定的变形，空仓的其余仓壁则几乎没有变形。这说明工作基仓仅对与之相连的仓壁产生一定影响，而对于不相连的仓壁则几乎没有影响，亦即对工作基仓起支撑作用的仅是与之相连的仓壁，而相隔的仓壁的支撑作用几乎可以忽略，如图23工况1、工况5。值得注意的是，工况7～工况12中，虽只有一个空仓而其余均为工作基仓，但并不是所有工作仓都同时发生局部屈曲，尽管蜂窝形钢筒仓的公共仓壁在相同高度处采用了相同的构件几何尺寸(如仓壁厚度等)，如图23所示工况10的屈曲模态，这说明仓壁的刚度不仅与其几何尺寸有关，而且也与基仓在群仓中的位置密切相关；显然这些部位的局部刚度较其余未屈曲仓壁偏小，因而先于屈曲。局部变形区域外的部位则基本保持原有形状。工况13代表了满仓工况，它的屈曲模态也间接印证了上述结论，不同之处在于，满仓工况时的局部屈曲可能在多处仓壁的底部发生，也不是所有工作基仓的仓壁均发生局部屈曲。

蜂窝形群仓结构在GMNA分析下的屈曲模态如图24所示，结构的屈曲模态也主要表现为仓壁壳单元和框架梁单元共同发生的整体弯曲变形，图中也仅给出了有代表性工况1、工况5、工况10、工况13时的屈曲模态。对工况1～工况6而言，它代表群仓中仅有一个工作基仓，而周围空仓对单个工作基仓的影响，由图可见，当工作基仓在群仓中所处位置不同时，结构的屈曲模态也变化较大；当工作基仓处于群仓的周边时，由于工作基仓存在多条仓壁未与其余基仓相连，因而这些仓壁的侧向刚度就弱很多，而工作基仓中与周围基仓相连仓壁的侧向刚度则大很多，表现在仓壁侧移上则是：未与周围基仓相连的工作基仓仓壁的平面外位移显著大于其余和周围基仓相连的工作基仓仓壁的平面外位移。如图中工况1所示工作基仓，其左侧平面外位移则显著大于右侧平面外位移，而对工况5而言，由于工作基仓周边均有其余空仓支撑，其六个仓壁的平面外位移几乎相同。另外，由于其余基仓对工作基仓产生一定的支撑作用，因而工作基仓也对周围与之相连的基仓的变形有一定影响，使相连的空仓仓壁产生附加变形。

工况7～工况12表示一个基仓为空仓而其余基仓为工作仓时，工作基仓对单个空仓的影响。这种情况下群仓的仓壁根据散料荷载的作用情况可分为两类，一类是公共仓壁，其两侧均有散料荷载作用，但由于两侧水平作用散料荷载方向相反，因而水平向的散料荷载理论上可以相互抵消，而仓壁两侧的竖向摩擦压力则由于叠加而成倍增大；另一类为单侧散料荷载作用的仓壁，在散料侧有水平散料压力和竖向摩擦压力同时存在。这两类仓壁的受力差异较大，对第一类仓壁而言，仓壁上主要存在竖向摩擦力，因而其平面外变形很小；对第二类仓壁而言，散料水平压力是影响结构屈曲的控制荷载。图24所示的屈曲模态表明，工作基仓的仓壁均发生整体弯曲变形，而与工作基仓相连的空仓仓壁也产生较大的附加变形，附加变形的大小和空仓在群仓中的位置密切相关。

工况13表示满仓工况，它的屈曲模态表现为群仓中周围各工作基仓共同发生弯曲变形；而公共仓壁由于两侧散料的水平压力基本相互抵消，因而其平面外侧移很小，群仓中处于中间位置的基仓变形则不明显，这也说明了对六边形蜂窝钢筒仓稳定性起控制作用的散料荷载为水平压力而不是竖向摩擦力。另外，蜂窝形群仓结构在几何非线性GNA分析下的屈曲模态基本与图24所示的同荷载工况的变形形状类似，此不赘述，该分析下的屈曲临界荷载系数见表1.7所示。

蜂窝形群仓结构各工况下非线性GMNA分析的荷载-位移全过程基本与图13类似，属于带肋平板的弯曲屈曲行为，但它的分析模型显得更加复杂，与上节研究的单仓结构和多仓组合结构相比，其曲线在第二阶段的荷载-位移响应的斜率变的更小，甚至难以追踪，数值模型分析的节点和单元显著增多，需要多次试算才能得到合理的结果。但蜂窝形筒仓荷载-位移曲线表示的屈曲过程仍属于平板弯曲屈曲的范畴。

4.2.2临界屈曲荷载系数

蜂窝形群仓结构在各分析工况下的线性和非线性屈曲临界荷载系数见表1.7所示，由表可见，线性屈曲LBA分析的临界屈曲荷载系数亦均远小于非线性屈曲分析，主要原因在于线性与非线性屈曲模态的显著差异，在线性屈曲中，结构的屈曲模态主要表现为单个或多个仓壁的局部屈曲，而群仓结构主要靠框架梁单元和壳体单元共同承受散料荷载的，因而结构的稳定承载力没有充分发挥，表现为临界屈曲荷载系数很小。非线性屈曲分析表明，几何非线性对结构的稳定承载力是有利的，与线性屈曲相比临界屈曲荷载系数约提高9～11倍；而GMNA分析时的材料非线性对结构的稳定承载力是显著不利的，与GNA分析相比，临界屈曲荷载系数约降低了约53％～54％。对蜂窝形钢筒仓而言，结构的屈曲分析应同时考虑几何非线性和材料非线性。

另外，蜂窝形群仓结构在各分析工况时的临界屈曲荷载系数也存在显著差别，对工况1～工况6，由于单个工作基仓受周围相连空仓的支撑作用，因而结构在这些工况下的GMNA屈曲临界荷载系数比上节研究的单仓一般要高80％以上；对工况6～工况12，多个工作基仓受单个空仓的支撑作用很小，而周围工作基仓对单仓的影响较大，因而这些工况在GMNA分析下的临界荷载屈曲系数与工况1～工况6相比小很多，其值一般约减小40％左右。工况13为满仓的情况，该工况在GMNA分析下的屈曲临界荷载系数最小，工况1～工况6时的临界荷载屈曲系数相比约减小45％～50％，亦即蜂窝形群仓时的最不利荷载工况为工况13，即满仓工况。

表1.7蜂窝形群仓结构的临界屈曲荷载系数λ_cr

5通过上述的分析得出本发明的有益效果是：

1)蜂窝形钢筒仓是一种新型的结构形式，它采用薄壳单元和框架梁单元共同抵抗散料荷载的结构体系-框壳结构。它与带加劲肋圆形钢筒仓有着本质的区别，带加劲肋的圆形钢筒仓中，仓壁壳单元为主要受力构件，而加劲肋仅是为了提高结构的整体或局部稳定承载力而设置的附加措施，因而本质上仍是薄壳结构。在框壳结构中，壳体单元与框架梁单元共同受力、协调变形，可以显著提高框架结构的整体刚度，特别是抗扭刚度，因而是一种可行的新型结构形式。

2)框壳结构的荷载-位移全过程与圆形钢筒仓结构的屈曲全过程有显著的差异，根据框壳结构荷载-位移全过程响应的特点，结构屈曲的过程可分为三个典型的阶段：线性阶段，强化阶段，衰减阶段。蜂窝形钢筒仓框壳结构的屈曲本质上属于平板结构的弯曲屈曲行为。

3)仓壁散料竖向摩擦力是引起圆形钢筒仓仓壁失稳的最主要因素，仓壁散料水平压力主要引起圆形钢筒仓仓壁周向拉应力，因而在弹性范围内它对结构的稳定是有利的。在六边形钢筒仓中，散料水平压力使仓壁产生较大的弯曲应力，水平压力对结构屈曲的影响一般比竖向摩擦力更为显著。对圆形钢筒仓稳定有利的散料水平内压，在六边形钢筒仓中成为最不利荷载且为稳定设计的主要控制荷载。

4)蜂窝形群仓的荷载工况不但随基仓个数的增加而显著增加，还与各基仓在群仓中排列的相对位置有关；群仓中基仓个数越多，结构分析应考虑的荷载工况越多。因而确定结构分析的控制工况是有必要且具有现实意义的。对组合群仓和蜂窝形群仓的分析表明，对结构的屈曲分析起控制的工况是满仓工况。

5)组合群仓和蜂窝形仓的屈曲承载力是由其组成单元，即六边形基仓的稳定承载力控制的。因而对组合群仓和蜂窝形群仓中的单仓可采用相同设计，并简化为单个六边形基仓的设计，然后再根据群仓和蜂窝仓的平面布置组合成设计形状。

6)与大直径圆形钢筒仓相比，六边形蜂窝仓可实现充分高效的利用土地。蜂窝形钢筒仓的最大优点是多个六边形钢筒仓的集束式建造，由于仓壁是平面的，因此不再需要钢板的弯曲。另外，仓壁所采用的钢板厚度多在20mm以内，与圆形钢筒仓相比其加工制作更加简单且施工质量更容易保证，施工更方便、建造周期缩短。

7)蜂窝形钢筒仓具有显著优于大直径圆形钢筒仓的特点：大直径圆形钢筒仓采用带仓底卸料口的多点卸料方式，因而它的稳定性主要是由大偏心卸料工况控制的。蜂窝形钢筒仓也可采用仓底的多点卸料方式，各基仓可同时或单独装卸料。基仓卸料时产生的散料荷载对蜂窝形群仓的影响范围十分有限。基仓卸料口与蜂窝仓形心之间的偏心甚至大偏心对蜂窝形钢筒仓的影响是很小的。