一种产生弯曲与轴向耦合振动带隙的周期梁的制作方法

本发明涉及振动控制领域，尤其涉及一种产生弯曲与轴向耦合振动带隙的周期梁。

背景技术：

振动对建筑结构、机械设备等的危害包括降低设备性能、缩短寿命、造成结构破坏等。至今人们仍在不断探索如何更有效的消除和控制有害振动。一般来说，要消除或减小振动，可以控制和减小振源的能量输出及频率范围，或改变和减少振动的传播途径，亦或改变受振动物体的动力特性。目前应用较多的减振和隔振技术，即分别针对振源和传播途径进行。这些技术一般依赖特别构造的阻尼器、隔振器、减振器等。但这些技术，由于大多不能精确针对实际需要控制的振动频率范围，其减振或隔振较为分散，效果并不理想。

近年来，声子晶体概念的出现为精确消除特定频率范围振动展现了新的策略。声子晶体是类比晶体、光子晶体提出的概念。它在宏观结构上具有类似晶体的周期性。特定的材料或几何的周期性排列，使弹性波或振动在其中传播的频散关系中在特定频率范围发生断裂，即出现了所谓的弹性波带隙或振动带隙。这意味着相应的弹性波或振动无法存在于该声子晶体中，理论上可实现带隙频率范围内振动的完美消除。

梁结构是极为重要的承载构件，在建筑结构、机械设备中均有普遍应用。梁可传递轴力、剪力、弯矩，故梁受到激励发生振动时，振动将以轴向振动、弯曲振动、扭转振动等的形式在其中传播，进而使振动波及与其相连的各处发生不同形式的振动甚至损坏。因此，若能利用声子晶体概念，使梁隔离激励的作用，将可极大减小结构、设备受振动发生破坏、缩短寿命、性能降低等危害。可实现对承载与消除振动的兼顾。

但对于梁而言，其中可传播的振动包括弯曲振动、轴向振动、扭转振动等，且一般声子晶体梁的弯曲振动带隙、轴向振动带隙、扭转振动带隙并不相关联。尤其是对梁影响最大的弯曲振动和轴向振动，相应的弯曲振动带隙与轴向振动带隙，频率范围相差很大，难以同时发挥作用。故一般声子晶体梁很难实现较好的实际减振效果。

技术实现要素：

发明目的：本发明的目的是提供一种通过产生弯曲与轴向耦合振动带隙，从而实现弯曲振动和轴向振动同时消除的周期梁。

技术方案：本发明所述的一种产生弯曲与轴向耦合振动带隙的周期梁，所述周期梁由多个相同的三折线梁在同一平面内首尾连接而成，所述三折线梁由首、中、末三段直线段梁在同一平面内首尾连接而成(类似Z形或者倒Z形)，其中，该三折线梁的首、末段平行且等长，中间段长度为首、末段长度的两倍，相邻的三折线梁的首、尾段连接成直线段。上述直线段梁在连接时的长度损耗误差忽略不计，所形成的周期梁以一个三折线梁为一周期，轴向延伸，周期数越多，其产生带隙效果越好。

进一步的，所述三折线梁的首尾端距离(即周期梁一周期的长度)为0.0001～5m。

进一步的，所述三折线梁的折点到首尾端连接线的距离比首尾端距离(即该周期梁的半高度比周期长度)为0.02～5:1。

进一步的，所述三折线梁的截面形状为圆形、矩形、圆环形和框形中的一种。

进一步的，所述三折线梁一体成型或者由直线段梁刚性连接而成，所述周期梁一体成型或者由三折线梁刚性连接而成，可以根据实际生产和后续安装的需要选择不同的形式。

进一步的，上述刚性连接为螺栓连接、焊接和粘结剂连接中的一种或多种。

进一步的，所述三折线梁采用金属或聚合物或者其他均质材料制成，由于声子晶体本身可依靠材料参数和结构参数的变化来调控振动带隙的频率范围，所以可以根据工程实际环境选用不同的材料和结构参数，使本发明的周期梁产生覆盖不同频率范围的弯曲与轴向耦合振动带隙，从而同时消除该频率范围内的弯曲振动与轴向振动。

工作原理：自低频到高频，均质直梁的平面内弯曲波与轴向波的频散曲线中有若干交点，代表两种波动的简并态，即同一频率对应一种弯曲波和一种轴向波。若将频率最低的简并态消除，即可打开一条同时对弯曲波与轴向波有效的带隙。但由于均质直梁的平面内弯曲波与轴向波是相互独立的，故虽然存在所述简并态，但绝无将其消除的可能。为了将所述兼并态消除，通过将梁设为特定形状(类似Z形或者倒Z形)，实现弯曲波与轴向波的耦合，由此，弯曲波与轴向波不再相互独立；进而，通过连接所述特定形状(类似Z形或者倒Z形)构造周期梁，使弯曲波与轴向波成为布洛赫波，由此，满足了通过消除弯曲波与轴向波简并态产生带隙的基本条件。该带隙即为弯曲与轴向耦合振动带隙。

有益效果：与现有技术相比，本发明的优点为：(1)通过将常规材料构成的直梁进行特定形状(类似Z形或者倒Z形)的周期性组合连接形成的周期梁，可以产生弯曲与轴向耦合振动带隙，从而实现对周期梁整体所在平面延伸方向上弯曲振动和轴向振动的共同控制与消除；(2)可以根据工程环境实际需求选择材料和结构参数产生特定频率范围内的弯曲与轴向耦合振动带隙，从而共同控制和消除该特定频率范围内的弯曲振动和轴向振动，且构造简单，易于实现。

附图说明

图1为本发明的周期梁立体结构示意图；

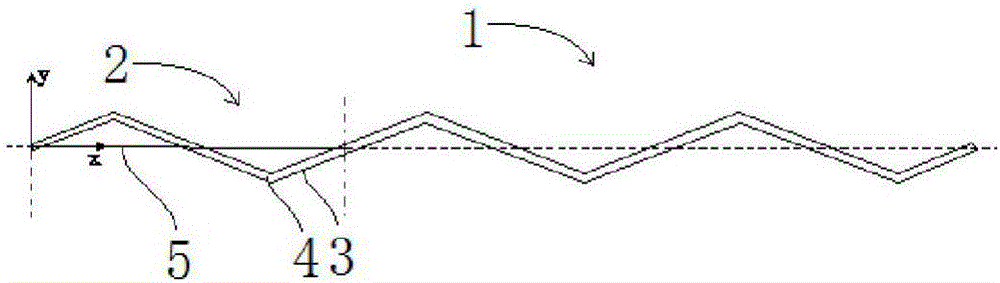
图2为本发明的周期梁平面结构示意图；

图3为本发明的三折线梁结构示意图；

图4为本发明的周期梁采用实施例1中的材料与结构参数，且为无限周期时，周期梁平面内弯曲与轴向振动的频散关系图；

图5为本发明的周期梁采用实施例1中的材料与结构参数，且周期数为16的情况下在周期梁所在平面内入射垂直于梁整体延伸方向振动的频率响应函数图；

图6为本发明的周期梁采用实施例1中的材料与结构参数，且周期数为16的情况下在周期梁所在平面内入射沿梁整体延伸方向振动的频率响应函数图；

图7为本发明的周期梁采用实施例2中的材料与结构参数，且为无限周期时，周期梁平面内弯曲与轴向振动的频散关系图；

图8为本发明的周期梁采用实施例2中的材料与结构参数，且周期数为20的情况下在周期梁所在平面内入射垂直于梁整体延伸方向振动的频率响应函数图；

图9为本发明的周期梁采用实施例2中的材料与结构参数，且周期数为20的情况下在周期梁所在平面内入射沿梁整体延伸方向振动的频率响应函数图；

图10为本发明的周期梁采用实施例3中的材料与结构参数，且为无限周期时，周期梁平面内弯曲与轴向振动的频散关系图；

图11为本发明的周期梁采用实施例3中的材料与结构参数，且周期数为25的情况下在周期梁所在平面内入射垂直于梁整体延伸方向振动的频率响应函数图；

图12为本发明的周期梁采用实施例3中的材料与结构参数，且周期数为25的情况下在周期梁所在平面内入射沿梁整体延伸方向振动的频率响应函数图。

具体实施方式

下面结合附图对本发明的技术方案作进一步说明。

实施例1

本发明的一种产生弯曲与轴向耦合振动带隙的周期梁，如图1所示，该周期梁1由16个相同的三折线梁2在同一平面内首尾连接而成(即该周期梁的周期数为16)，所述三折线梁2由首、中、末三段直线段梁3在同一平面内首尾连接而成，其中，该三折线梁2的首、末段平行且等长，中间段长度为首、末段长度的两倍，相邻的三折线梁2的首、尾段连接成直线段。如图2所示，所形成的周期梁以一个三折线梁为一周期，沿X轴方向延伸。

如图3所示，所述三折线梁2的首尾端距离(即该周期梁的周期长度)为0.1m，且其折点4到首尾端连接线5的距离比首尾端距离(即该周期梁的半高度比周期长度)为0.1:1。

所述三折线梁2的截面形状为矩形，该矩形长宽均为0.002m。

所述三折线梁2由直线段梁3焊接而成，所述周期梁1由三折线梁2螺栓连接而成。

所述三折线梁2采用密度为2730kg·m^-3,弹性模量为7.76×10¹⁰Pa的铝。

在对本实施例所限定的结构做数据模拟时，先将其周期数选为无限周期(此为理想情况)，再在0～5000Hz内进行弯曲与轴向振动频散关系模拟，模拟结果如图4所示，在776～1759Hz范围内出现了明显的弯曲与轴向耦合振动带隙，理想情况下，在此范围内，任何弯曲振动与轴向振动都是禁止的。

对本实施例周期梁周期数为16的情况下进行频率响应模拟，在周期梁所在平面内入射垂直于梁整体延伸方向的振动(即弯曲振动)得到频率响应函数图，如图5所示。

对本实施例周期梁周期数为16的情况下进行频率响应模拟，在周期梁所在平面内入射沿梁整体延伸方向的振动(即轴向振动)得到频率响应函数图，如图6所示。

如图5所示，16周期的梁结构的弯曲振动频率响应函数在777～1761Hz范围内衰减明显，最低接近-150dB，证明弯曲振动在此频率范围的传播收到了阻碍，几乎不能通过；如图6所示，16周期的梁结构的轴向振动频率响应函数在777～1759Hz范围内衰减明显，最低接近-150dB，证明轴向振动在此频率范围的传播受到了阻碍，几乎不能通过，所以显然，弯曲振动与轴向振动在几乎相同的频率范围受到了阻碍，且该范围与图4所示的理想情况下的带隙范围一致，及弯曲振动带隙与轴向振动带隙发生耦合，当该周期梁的周期数目足够时，其与理想情况下无限周期结构的振动特征十分接近，同时也验证了图4、图5和图6的正确性。

实施例2

该周期梁1由20个相同的三折线梁2在同一平面内首尾连接而成(即该周期梁的周期数为20)，所述三折线梁2由首、中、末三段直线段梁3在同一平面内首尾连接而成，其中，该三折线梁2的首、末段平行且等长，中间段长度为首、末段长度的两倍，相邻的三折线梁2的首、尾段连接成直线段。如图2所示，所形成的周期梁以一个三折线梁为一周期，沿X轴方向延伸。

如图3所示，所述三折线梁2的首尾端距离(即该周期梁的周期长度)为0.0001m，且其折点4到首尾端连接线5的距离比首尾端距离(即该周期梁的半高度比周期长度)为5:1。

所述三折线梁2的截面形状为圆形，该圆形直径为0.00001m。

所述三折线梁2由直线段梁3螺栓连接而成，所述周期梁1由三折线梁2焊接而成。

所述三折线梁2采用密度为1180kg·m^-3,弹性模量为0.435×10¹⁰Pa的环氧树脂。

在对本实施例所限定的结构做数据模拟时，先将其周期数选为无限周期(此为理想情况)，再在0～30000Hz内进行弯曲与轴向振动频散关系模拟，模拟结果如图7所示，在2676～16672Hz与17064～27231Hz范围内出现了明显的弯曲与轴向耦合振动带隙，理想情况下，在此范围内，任何弯曲振动与轴向振动都是禁止的。

对本实施例周期梁周期数为20的情况下进行频率响应模拟，在周期梁所在平面内入射垂直于梁整体延伸方向的振动(即弯曲振动)得到频率响应函数图，如图8所示。

对本实施例周期梁周期数为20的情况下进行频率响应模拟，在周期梁所在平面内入射沿梁整体延伸方向的振动(即轴向振动)得到频率响应函数图，如图9所示。

如图8所示，20周期的梁结构的弯曲振动频率响应函数在2670～16680Hz与17060～27200Hz范围内衰减明显，最低低于-60dB，证明弯曲振动在此频率范围的传播收到了阻碍，几乎不能通过；如图9所示，20周期的梁结构的轴向振动频率响应函数在2670～16670Hz与17090～27580范围内衰减明显，最低低于-120dB，证明轴向振动在此频率范围的传播受到了阻碍，几乎不能通过，所以显然，弯曲振动与轴向振动在几乎相同的频率范围受到了阻碍，且该范围与图7所示的理想情况下的带隙范围一致，及弯曲振动带隙与轴向振动带隙发生耦合。

实施例3

该周期梁1由25个相同的三折线梁2在同一平面内首尾连接而成(即该周期梁的周期数为25)，所述三折线梁2由首、中、末三段直线段梁3在同一平面内首尾连接而成，其中，该三折线梁2的首、末段平行且等长，中间段长度为首、末段长度的两倍，相邻的三折线梁2的首、尾段连接成直线段。如图2所示，所形成的周期梁以一个三折线梁为一周期，沿X轴方向延伸。

如图3所示，所述三折线梁2的首尾端距离(即该周期梁的周期长度)为5m，且其折点4到首尾端连接线5的距离比首尾端距离(即该周期梁的半高度比周期长度)为0.02:1。

所述三折线梁2的截面形状为环形，该环形外直径为0.0005m，内径为0.0003m。

所述三折线梁2一体成型，所述周期梁1一体成型。

所述三折线梁2采用密度为7800kg·m^-3,弹性模量为21.0×10¹⁰Pa的钢。

在对本实施例所限定的结构做数据模拟时，先将其周期数选为无限周期(此为理想情况)，再在0～2.5Hz内进行弯曲与轴向振动频散关系模拟，模拟结果如图10所示，在1.373～1.896Hz范围内出现了明显的弯曲与轴向耦合振动带隙，理想情况下，在此范围内，任何弯曲振动与轴向振动都是禁止的。

对本实施例周期梁周期数为25的情况下进行频率响应模拟，在周期梁所在平面内入射垂直于梁整体延伸方向的振动(即弯曲振动)得到频率响应函数图，如图11所示。

对本实施例周期梁周期数为25的情况下进行频率响应模拟，在周期梁所在平面内入射沿梁整体延伸方向的振动(即轴向振动)得到频率响应函数图，如图12所示。

如图11所示，25周期的梁结构的弯曲振动频率响应函数在1.380～1.905Hz范围内衰减明显，最低接近-90dB，证明弯曲振动在此频率范围的传播收到了阻碍，几乎不能通过；如图12所示，25周期的梁结构的轴向振动频率响应函数在1.375～1.904Hz范围内衰减明显，最低接近-90dB，证明轴向振动在此频率范围的传播受到了阻碍，几乎不能通过，所以显然，弯曲振动与轴向振动在几乎相同的频率范围受到了阻碍，且该范围与图10所示的理想情况下的带隙范围一致，及弯曲振动带隙与轴向振动带隙发生耦合。