一种六自由度机械臂考虑力约束的轨迹规划方法与流程

本发明属于机械臂迹规划领域，具体涉及一种六自由度机械臂考虑力约束的轨迹规划方法。

背景技术：

机械臂轨迹规划是指在规定时间内，机械臂按照一定的速度和加速度完成从初始位置姿态运动到期望位置姿态的运动。机械臂考虑力约束的轨迹规划是使得机械臂在期望力的约束下，让六自由度机械臂实现期望轨迹的规划。基于力约束的机械臂轨迹规划有很多方法，如4-3-4轨迹，3-5-3轨迹以及5段3次轨迹等，这些方法均可进行处理机械臂动力约束下的轨迹规划，但面向关节空间的笛卡尔路径会损失部分采样点。

本发明提出的方法针对一类典型的六自由度机械臂，工业机械臂大部分属于此类机械臂，因此对于这类机械臂考虑力约束的轨迹规划的研究具有很大的意义。

技术实现要素：

本发明的目的在于提供一种考虑接触形变基于不同接触边缘的六自由度机械臂考虑力约束的轨迹规划方法。

本发明的目的是这样实现的：

1.一种六自由度机械臂考虑力约束的轨迹规划方法，其特征在于，包括如下步骤：

(1)将力约束转化为接触形变和接触运动速度的约束；

根据接触模型将机械臂末端与环境的接触分为静态接触和动态接触；

(1.1)静态接触过程中，将力的约束转化为沿法线方向的接触位移的约束，即

$X_E=\sqrt{F/K_s}\≤\sqrt{F_{max}/K_s}=X_{Emax}$

其中，K_s是接触刚度；X_E是机械臂末端沿接触面法向的形变量；F表示机械末端力传感器测量的接触面法线方向上的接触力；

(1.2)动态接触也就是冲击，机械臂末端与外界环境的接触碰撞过程在极短的时间内完成，将力约束转化为接触速度的约束，来实现满足机械臂轨迹规划过程中冲击最优；

(2)优化动态接触冲击的机械臂运动速度；

(2.1)采用S型加减速曲线使加速度连续；

采用S型速度变化使得运动过程中加速度连续，减小各关节的冲击，使机械臂运动和作业满足力的约束；

优化后的S型速度曲线共分为七个过程：

(2.1.1)加加速度一定、加速度匀速增加过程，加速度从初始值加速到最大加速度；

(2.1.2)匀加加速度加速过程，保持最大加速度不变，速度匀速增加；

(2.1.3)减加速度加速过程，速度继续增加，加速度以恒定的加加速度减小直到速度加到最大速度值；

(2.1.4)匀速运动过程，保持最大速度运动，加速度为零；

(2.1.5)减减速度减速过程，速度减小，减速度以恒定的减减速度减小；

(2.1.6)匀减减速度减速过程，保持减速度不变，速度匀速减小；

(2.1.7)减减速度一定减速度匀速减小过程；

(2.2)归一化时间算子；

笛卡尔空间位置插补的表达式为：

P(t)＝P_s+l(t)(P_e-P_s)，

其中，P(t)表示插补点的坐标；l(t)为归一化时间算子；P_s为期望位置；P_e为初始位置；

要对时间算子进行平滑处理，使得速度曲线平滑，定义归一化时间算子的表达式为：

$l\left(t\right)=\frac{S\left(t_{i+1}\right)-S\left(t_i\right)}{L},$

其中，i＝0,1,2,3,4,5,6；l(0)＝0；l(T)＝1；l(t)在区间内单调递增；S(t)为各时间段内对应的总位移；

(3)基于力约束进行轨迹规划；

(3.1)基于规则接触边缘具有力约束的连续轨迹规划：

规则接触边缘具有力约束的连续轨迹采用圆弧过渡的方法代替直线-直线连续轨迹规划方法进行平滑处理，达到运动在接触临界接触面时不具有沿接触面法线方向的位移、速度和加速度分量，过渡圆弧的联结点分别选取在前一段直线的减速段和后一段直线的加速段；

(3.1.1)在接触模型有效的情况下，得到机械臂末端与外界环境的接触刚度为K，在已知约束力为F的情况下，可求得接触形变X_e：

X_e＝F/K；

(3.1.2)通过接触形变，得到临界接触点B点的空间位置坐标p₂：

p₂＝p_q+X_e；

轨迹终点M的空间位置坐标p₃为：

p₃＝p₂+L；

(3.1.3)过渡精度的确定，过渡精度决定过渡圆弧的大小，决定实际轨迹与期望轨迹逼近程度；设过渡力大小为F'，则过渡精度re为：

re＝F-F'

当力传感器示数时，进行空间直线轨迹运动；当力传感器示数时，为过渡圆弧的起点；当力传感器示数时，进行圆弧过渡运运动；当力传感器示数时，为过渡圆弧的终点，之后机械臂末端与外界环境保持力F进行沿接触面切平面方向的运动；

(3.1.4)确定过渡圆弧起始联结点p_e1和过渡圆弧终止联结点p_e2；

当力传感器示数到达过渡力F'时开始圆弧过渡运动，当力传感器示数到达约束力F时结束圆弧过渡运动；即过渡圆弧联结点为接触力为F'和F时机械臂末端的位置点；

当力传感器示数时，通过位置编码器可知当前机械臂六个关节关节角θ_e11～θ_e16，通过机械臂正运动学式得到此刻对应的机械臂末端实际位置即为过渡圆弧起始联结点p_e¹；当力传感器示数时，通过位置编码器可知当前机械臂六个关节关节角θ_e21～θ_e26，通过机械臂正运动学式得到此刻对应的机械臂末端实际位置即为过渡圆弧终止联结点p_e2；

(3.1.5)轨迹生成器通过路径点和过渡圆弧起始联结点p_e1和终止联结点p_e2的空间位置坐标，采用具有S型速度曲线拟合的空间直线和圆弧规划方法生成运动轨迹；

(3.1.6)运动过程中用力传感器进行监测，看整个运动过程是否满足期望力F的约束，如果时，重新规划。

(3.2)基于曲率接触边缘具有力约束的连续轨迹规划：

(3.2.1)机械臂实现沿接触面法线方向直线运动和沿临界安全接触面的接触运动和沿接触面法线方向远离临界安全接触面的直线运动，是一个直线-圆弧-直线连续的轨迹规划过程，确定运动过程中在安全接触圆柱面上的具有力约束运动中的特殊点M、N点；

(3.2.2)采用圆弧过渡来解决直线-圆弧连续运动时产生的尖角问题；使得末端在沿安全接触面的运动过程中只有沿接触面切线方向位移和速度，法线方向速度为零；

(3.2.3)通过调节过渡精度来调整实际轨迹与期望轨迹的精度，满足接触模型的基于圆柱接触面的连续轨迹规划方法与基于规则接触面连续轨迹规划方法中过渡圆弧联结点求取方法一致，过渡完后机械臂末端是在一定接触力下沿着接触面的圆弧轨迹。

本发明的有益效果在于：

本发明将机械臂力约束转化为接触形变和接触运动速度的约束，再根据接触运动学，提出了动态接触冲击的机械臂运动速度优化方法和考虑接触形变的基于不同接触边缘的连续轨 迹规划方法，此方法为考虑力约束的机械臂轨迹规划提供了新方法。此方法避免了机械臂末端与外界环境的接触碰撞过程在极短时间内完成，产生极大瞬间冲击，导致接触力超出安全范围。

附图说明

图1是机械臂具有力约束轨迹规划系统结构图；

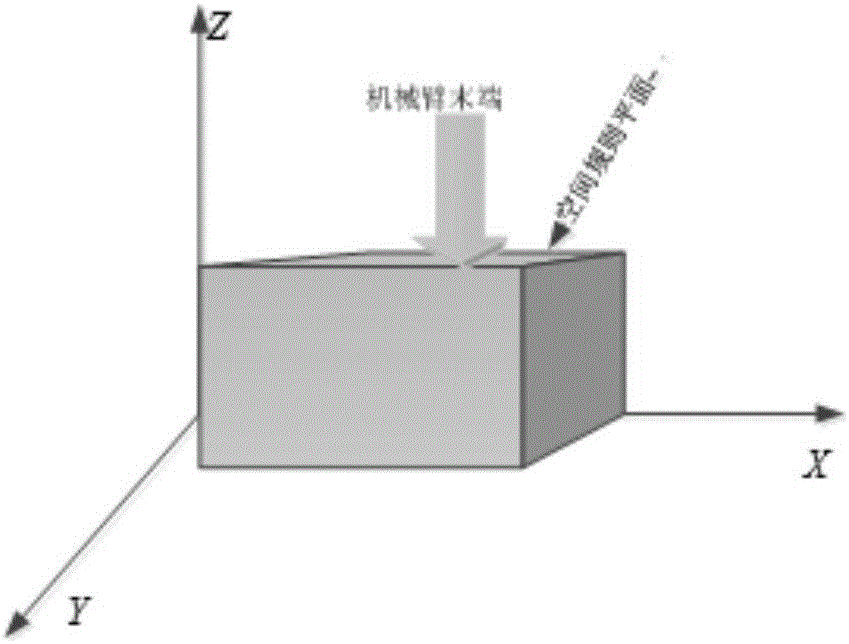
图2是机械臂末端与规则接触面示意图；

图3是基于规则接触面具有力约束轨迹规划示意图；

图4是机械臂末端与具有曲率接触面示意图。

具体实施方式

下面结合附图对本发明做进一步描述。

本发明提供的是一类六自由度机械臂考虑力约束的轨迹规划方法，属于机械臂轨迹规划领域。传统六自由度机械臂轨迹规划时，只考虑机械臂末端的位置而对力约束的轨迹规划研究很少，但此类问题尤为重要，针对这一现状，本发明提出一类六自由度机械臂考虑力约束的轨迹规划方法。本发明提出的机械臂考虑力约束的轨迹方法如下：首先利用接触模型和接触运动学将力约束转化为接触形变和接触运动速度的约束，然后在优化动态接触冲击的轨迹规划中，对运动速度进行S型曲线处理，最后提出对基于规则接触边缘和基于曲率接触边缘的具有力约束的连续轨迹规划方法，一种在力的过渡阈值范围内，采用法线方向接触运动向切线方向接触运动过渡的且具有S型速度曲线的连续轨迹规划方法。此方法避免机械臂与外界环境的接触过程中产生过大冲击造成超出约束要求，且适用于具有力约束的六自由度机械臂的轨迹规划，在不同接触边缘提出不同轨迹规划，更大程度的满足现代工程项目对工业机械臂轨迹规划的要求。

一类六自由度机械臂考虑力约束的轨迹规划方法，包括如下步骤：

1、将力约束转化为接触形变和接触运动速度的约束

接触力不仅与接触形变有关，还与接触过程中的冲击有关，于是接触模型可将机械臂末端与环境的接触分为静态接触和动态接触。

⑴静态接触作用时间较长，接触状态变化缓慢匀速或保持不变，接触过程中，可将力的约束转化为沿法线方向的接触位移的约束，即

$X_E=\sqrt{F/K_s}\≤\sqrt{F_{max}/K_s}=X_{Emax}$

其中，K_s是接触刚度，与材料有关；X_E是机械臂末端沿接触面法向的形变量；F表示机械末端力传感器测量的接触面法线方向上的接触力；

⑵动态接触也就是所说的冲击，机械臂末端与外界环境的接触碰撞过程在极短的时间内完成，在此过程中可将力约束转化为接触速度的约束，来实现满足机械臂轨迹规划过程中冲击最优。

2、优化动态接触冲击的机械臂运动速度

⑴采用S型加减速曲线

采用S型速度变化使得运动过程中加速度连续，进而减小各关节的冲击，使机械臂运动和作业满足力的约束。

优化后的S型速度曲线共分为七个过程：

①加加速度一定加速度匀速增加过程，加速度从初始值加速到最大加速度；

②匀加加速度加速过程，此过程中保持最大加速度不变，速度匀速增加；

③减加速度加速过程，此过程中速度继续增加，加速度以恒定的加加速度减小直到速度加到最大速度值；

④匀速运动过程，此过程中保持最大速度运动，加速度为零；

⑤减减速度减速过程，此过程中速度减小，减速度以恒定的减减速度减小；

⑥匀减减速度减速过程，此过程中保持减速度不变，速度匀速减小；

⑦减减速度一定减速度匀速减小过程；

⑵归一化时间算子

笛卡尔空间位置插补的表达式为：

P(t)＝P_s+l(t)(P_e-P_s)

其中，P(t)表示插补点的坐标；l(t)为归一化时间算子；P_s为期望位置；P_e为初始位置。

要对时间算子进行平滑处理，使得速度曲线平滑。定义归一化时间算子的表达式为：

$l\left(t\right)=\frac{S\left(t_{i+1}\right)-S\left(t_i\right)}{L}$

其中，i＝0,1,2,3,4,5,6；l(0)＝0；l(T)＝1；l(t)在区间内单调递增；S(t)为各时间段内对应的总位移；

3、基于力约束进行轨迹规划

⑴基于规则接触边缘具有力约束的连续轨迹规划：

规则接触边缘具有力约束的连续轨迹采用圆弧过渡的方法代替直线-直线连续轨迹规划方法进行平滑处理。达到运动在接触临界接触面时不具有沿接触面法线方向的位移、速度和加速度分量，过渡圆弧的联结点分别选取在前一段直线的减速段和后一段直线的加速段。

①在接触模型的有效的情况下，可得机械臂末端与外界环境的接触刚度为K，在已知约 束力为F的情况下，可求得接触形变X_e：

X_e＝F/K

②通过接触形变，可得临界接触点B点的空间位置坐标p₂：

p₂＝p_q+X_e

轨迹终点M的空间位置坐标p₃为：

p₃＝p₂+L

③过渡精度的确定，过渡精度决定过渡圆弧的大小，决定实际轨迹与期望轨迹逼近程度。设过渡力大小为F'，则过渡精度re为：

re＝F-F'

当力传感器示数时，进行空间直线轨迹运动；当力传感器示数时，为过渡圆弧的起点；当力传感器示数时，进行圆弧过渡运运动；当力传感器示数时，为过渡圆弧的终点，之后机械臂末端与外界环境保持力F进行沿接触面切平面方向的运动。

④确定过渡圆弧联结点p_e1和p_e2。

当力传感器示数到达过渡力F'时开始圆弧过渡运动，当力传感器示数到达约束力F时结束圆弧过渡运动。即过渡圆弧联结点为接触力为F'和F时机械臂末端的位置点。

当力传感器示数时，通过位置编码器可知当前机械臂六个关节关节角θ_e11～θ_e16，通过机械臂正运动学式可得此刻对应的机械臂末端实际位置即为过渡圆弧起始联结点p_e1。同理，当力传感器示数时，通过位置编码器可知当前机械臂六个关节关节角θ_e21～θ_e26，通过机械臂正运动学式可得此刻对应的机械臂末端实际位置即为过渡圆弧终止联结点p_e2。

⑤轨迹生成器通过路径点和过渡圆弧起始联结点p_e1和终止联结点p_e2的空间位置坐标，采用具有S型速度曲线拟合的空间直线和圆弧规划方法生成运动轨迹。

⑥运动过程中用力传感器进行监测，看整个运动过程是否满足期望力F的约束，如果 时，重新规划。

⑵基于曲率接触边缘具有力约束的连续轨迹规划：

①机械臂实现沿接触面法线方向直线运动和沿临界安全接触面的接触运动和沿接触面法线方向远离临界安全接触面的直线运动，是一个直线-圆弧-直线连续的轨迹规划过程，运动过程中M、N点在安全接触圆柱面上，是具有力约束运动中的特殊点。

②采用圆弧过渡来解决直线-圆弧连续运动时产生的尖角问题。使得末端在沿安全接触面 的运动过程中只有沿接触面切线方向位移和速度，法线方向速度为零，保证运动满足安全约束。

③通过调节过渡精度来调整实际轨迹与期望轨迹的精度。满足接触模型的基于圆柱接触面的连续轨迹规划方法与基于规则接触面连续轨迹规划方法中过渡圆弧联结点求取方法一致，不同的是过渡完后机械臂末端是在一定接触力下沿着接触面的圆弧轨迹。

1、具有接触形变约束的轨迹规划方法

接触模型的接触刚度稳定不变，将力约束转化为接触位移的约束来实现机械臂末端与外界环境之间的安全接触运动。具有力约束轨迹规划系统结构图如附1图所示，整个系统结构由接触模型、轨迹生成器、力位混合控制器及机械臂执行器组成。其中，F_d为期望力约束；X_e为通过接触模型得到的接触形变；Y为实际位置；F为机械臂腕部六维力传感器测量的机械臂末端施加的力。

1)、接触模型

将力约束转化为接触形变的约束进行机械臂与外界环境之间接触运动。由接触模型式得出，接触力不仅与接触形变有关还与接触刚度有关。机械臂末端与外界环境之间的接触刚度与机械臂自身末端刚度和环境刚度有关。对于机械臂末端的刚度与其姿态有关，在保持末端位置不变的情况下不同姿态所对应的末端刚度不同；环境刚度与接触环境的材料有关。对于刚度较大的接触，较小的形变就会产生较大的接触力。因此，要想实现力约束的转化就先要对接触模型进行验证。

本发明将采用实验测量的方法对接触模型进行验证，具体步骤如下：

(1)选运动方向沿接触面法线方向，设定机械臂末端起始位置X₀，通过角位移编码器反馈读取当前实际六个关节角角位移值θ₁～θ₆，根据机械臂正运动学可知机械臂末端实际位置

(2)保持其他方向位移不变，让机械臂沿接触面法线方向运动期望距离ΔX_i，与外界环境产生接触，读取当前力传感器示数F_i和当前实际六个关节角角位移值θ_i1～θ_i6，根据机械臂正运动学可知机械臂末端实际位置进行多组数据测量，每次的期望运动距离可不同。

(3)对采集到的F_i和进行数据处理，验证两者是否满足线性关系，若满足则证明接触模型正确，进而可以得到接触刚度值，实现力约束向接触形变约束的转化。

2)、轨迹生成器

轨迹生成器可以根据所给的路径点生成期望轨迹。对于不同的环境不同的作业任务，机械臂末端与外界物体之间接触运动的轨迹不同，所选用的轨迹生成方法也不同。若要实现接触运动直线轨迹，则选用轨迹生成器中直线插补方法；若要求在接触运动过程中实现圆弧轨迹，则选择圆弧插补方法；要若要在接触过程中实现自由曲线轨迹，则选用样条函数插值方法。

接触运动学，当接触运动过程是沿切线方向运动和法线方向运动的组合运动时，不仅需要考虑轨迹的连续性还要使得整个运动过程在力的安全约束范围内。对于此要求，本发明将采用运动过渡的方法实现具有力约束的轨迹规划。在接触模型成立的基础上，可以将接触力的约束转化为接触形变约束，进而可以将力安全阈值范围转化为过渡轨迹。在有力约束的情况下，对于沿接触面法线方向运动与沿接触面切平面方向运动轨迹的过渡过程中，解决轨迹尖角问题是实现满足要求运动的关键。对于连续轨迹中的尖角问题处理有圆弧过渡和样条函数二次插补过渡两种方法。根据过渡轨迹要求不同可采取不同的过渡方法，样条函数二次插补适合对过渡轨迹精度要求较高或过渡轨迹曲线不确定的运动，相比圆弧过渡，样条函数二次插补过渡方法计算量大，效率低。因此，本文将采用圆弧过渡的方法实现具有力约束的轨迹规划。

由于机械臂末端刚度与机械臂末端姿态有关，姿态的变化会影响接触刚度的变化，导致末端接触力变化，末端姿态的变化还会产生与接触面之间滚动接触运动，使得机械末端与外界环境之间不仅有力的作用还有力矩的作用，是一个十分复杂的问题。本文这里假设运动过程中机械臂末端相对于接触环境的姿态保持不变即保持接触刚度不变，只考虑具有沿接触面法线方向力约束情况和与接触面之间滑动接触运动。

3)、力位混合控制器

轨迹生成器根据给定的路径点生成笛卡尔空间期望轨迹，并通过机械臂逆运动学转化为关节空间轨迹。将对应的关节变量输入给力位混合控制器，通过控制器实现机械臂运动。

2、基于规则接触边缘具有力约束的连续轨迹规划方法

本发明选择空间平面为规则接触面进行研究，图3机械臂末端与接触面的空间示意图。运动情况描述为：机械臂末端从空间起始点沿接触面法线方向运动到规则接触面，在具有一定接触力情况下沿着接触面运动。为了方面研究，将机械臂末端与环境的接触看作为点接触，接触过程中假设接触刚度不发生变化，研究滑动接触运动过程中连续轨迹规划方法。

在接触模型成立的情况下，由赫兹接触理论接触力的计算公式可知，在接触刚度一定，力指数为1的情况下，接触形变与接触力成线性关系。对于具有规则接触面的平面，已知最大接触力约束，可得规则接触平面对应的临界安全接触面是一个与规则接触面平行的平面如 图2所示。图2中，A为起始点，Q为接触面上的点，B、M为临界安全接触面上的点，要求机械臂末端实现沿接触面法线和接触面切平面连续直线轨迹规划任务，即AB-BM连续直线轨迹。在AB-BM连续轨迹中B点在临界安全接触面上，是满足力约束运动中的一个特殊点。

对于空间连续直线运动，理论上可以采取单独规划每条独立直线的方法，但是这样会使得电机在各段直线间不停的启动和停止，实际中这种操作会产生较大的振动和摩擦[51]。若进行连续的规划，由图2可以看出，在直线与直线的联结处即B点处会有尖角产生，尖角的存在会使得位移、速度方向发生突变，不但轨迹不平滑而且会造成运动超出安全接触形变的约束。对于此种情况，本文将采用圆弧过渡的方法对直线-直线连续轨迹进行平滑处理，过渡圆弧的联结点分别在前一段直线的减速段和后一段直线的加速段，圆弧过渡示意图如图2中轨迹所示，这样不仅可以保证B点的特殊要求，并使得运动在接触临界接触面时不具有沿接触面法线方向的位移、速度和加速度分量。

对于图3中所描述的运动，满足接触模型的基于规则接触平面的连续轨迹规划方法如下：

已知起始点A的位置坐标为p₁，外界接触物体上一点Q坐标p_q，期望约束力为F，沿接触面切平面运动距离为L。

(1)在接触模型的有效的情况下，可得机械臂末端与外界环境的接触刚度为K，在已知约束力为F的情况下，可求得接触形变X_e：

X_e＝F/K

(2)通过接触形变，可得临界接触点B点的空间位置坐标p₂：

p₂＝p_q+X_e

轨迹终点M的空间位置坐标p₃为：

p₃＝p₂+L

(3)过渡精度的确定，过渡精度决定过渡圆弧的大小，决定实际轨迹与期望轨迹逼近程度。设过渡力大小为F'，则过渡精度re为：

re＝F-F'

当力传感器示数时，进行空间直线轨迹运动；当力传感器示数时，为过渡圆弧的起点；当力传感器示数时，进行圆弧过渡运运动；当力传感器示数时，为过渡圆弧的终点，之后机械臂末端与外界环境保持力F进行沿接触面切平面方向的运动。

(4)确定过渡圆弧联结点p_e1和p_e2。

当力传感器示数到达过渡力F'时开始圆弧过渡运动，当力传感器示数到达约束力F时结束圆弧过渡运动。即过渡圆弧联结点为接触力为F'和F时机械臂末端的位置点。

当力传感器示数时，通过位置编码器可知当前机械臂六个关节关节角θ_e11～θ_e16，通过机械臂正运动学式可得此刻对应的机械臂末端实际位置即为过渡圆弧起始联结点p_e1。同理，当力传感器示数时，通过位置编码器可知当前机械臂六个关节关节角θ_e21～θ_e26，通过机械臂正运动学式可得此刻对应的机械臂末端实际位置即为过渡圆弧终止联结点p_e2。

(5)轨迹生成器通过路径点A、Q、M和过渡圆弧起始联结点p_e1和终止联结点p_e2的空间位置坐标，采用具有S型速度曲线拟合的空间直线和圆弧规划方法生成运动轨迹。

(6)运动过程中用力传感器进行监测，看整个运动过程是否满足期望力F的约束，如果 时，重新规划。

需要说明的是，在机械臂末端接触运动过程中会产生摩擦力，本文暂不考虑摩擦力的影响；对于不同接触刚度的物体，力约束下的接触形变大小不同，运动中可以通过调整过渡精度来调整跟期望轨迹的逼近程度。

3.基于曲率接触边缘具有力约束的连续轨迹规划方法

本发明选择圆柱体为具有一定曲率的接触面进行研究，图4为机械臂末端与接触面的空间示意图。运动情况描述为：机械臂末端从空间中起始点沿接触法线方向运动到规则接触面，在具有一定接触力情况下沿着接触面运动。为了方面研究，将机械臂末端与环境的接触看作为点接触，接触过程中假设接触刚度不发生变化，研究滑动接触运动过程中连续轨迹规划方法。

由赫兹接触理论接触力的计算公式可知，在接触刚度一定，力指数为1的情况下，接触形变与接触力成线性关系。对于圆柱接触面，已知最大安全接触力，可知临界安全接触面也是一个与圆柱面通圆心的圆柱面投影图4所示。只要接触运动过程中产生的位移不超过临界安全接触面，即可使运动满足力的约束。图中A为起始点，Q为接触面上的点，M、U、N为临界安全接触面上的点，要求机械臂实现沿接触面法线方向直线运动和沿临界安全接触面的接触运动和沿接触面法线方向远离临界安全接触面的直线运动，即AM-MN-NB运动，是一个直线-圆弧-直线连续的轨迹规划过程，运动过程中M、N点在安全接触圆柱面上，是具有力约束运动中的特殊点。规划的关键是解决直线与圆弧连接时在接触点出现的尖角问题，进而解决特殊点位置、速度、加速度约束问题，使得运动满足安全要求。本发明采用圆弧过渡来解决直线-圆弧连续运动时产生的尖角问题，如图4中蓝色轨迹所示。这样使得末端在沿 安全接触面的运动过程中只有沿接触面切线方向位移和速度，法线方向速度为零，保证运动满足安全约束。可通过调节过渡精度来调整实际轨迹与期望轨迹的精度。满足接触模型的基于圆柱接触面的连续轨迹规划方法与基于规则接触面连续轨迹规划方法中过渡圆弧联结点求取方法一致，不同的是过渡完后机械臂末端是在一定接触力下沿着接触面的圆弧轨迹。