一种基于视觉辅助定位的机器人自标定方法与流程

本发明涉及一种机器人自标定方法，特别涉及一种基于平面约束以及视觉辅助定位的机器人自标定方法。

背景技术：

1.机器人定位精度是衡量其工作性能的一个重要指标，目前，国内外厂家生产出来的机器人由于制造、安装等因素，大多绝对定位精度不高，无法满足高精加工以及离线编程的需要，因此，对引起机器人定位误差的各种因素进行分析，最大可能地提高机器人绝对定位精度已经成为机器人技术研究中的核心内容。

2.目前，国内外常用的机器人标定方法通常需要借助于外界先进的测量设备，成本高，且测量过程复杂，需要专业人员进行操作；同时，由于涉及到测量坐标系与机器人基坐标系的转换过程，容易引入坐标系环误差，且该误差与机器人连杆参数误差不属于同类误差，需要单独处理，过程较复杂。

3.为了降低成本等因素，很多研究人员提出了闭环法标定，即给机器人末端附加一约束，用的较多的是面约束(平面或球面)，然而在对这些面进行接触式测量时，大多采用人工手动示教的方式，测量过程费时费力，效率很低。

4.针对上述技术情况，本发明在一般平面约束(手动示教进行接触式测量)的基础上，提出一种基于视觉辅助定位的机器人自标定方法。

技术实现要素：

针对上述现有技术存在的不足，本发明在一般平面约束(手动示教进行接触式测量)的基础上，提供一种基于视觉辅助定位的机器人自标定方法，该方法通过双目视觉定位约束平面的位置，输入到机器人控制系统，控制机器人自动对约束平面进行接触式测量，在继承一般平面约束标定方法优点的同时，又大大提高了标定效率，并且，可通过编程使约束点按一定规律有序排列，可为后期研究约束点对机器人标定结果的影响奠定基础。

本发明技术方案步骤如下：

(1)建立机器人运动学模型

建立d-h法与md-h法相结合的机器人运动学模型，将坐标系i-1到坐标系i的变换过程描述为ai，ai＝f(αi-1,ai-1,di,θi,βi)，则机器人末端坐标系n相对于基坐标系的位姿矩阵⁰tn为：

⁰tn＝a0·a1·...·an

(2)建立机器人末端位置误差模型

按照微分变换的思想对ai进行全微分，得到由连杆几何参数误差造成的相邻坐标系间的微分摄动齐次矩阵dai：

δai是关节坐标系i相对于坐标系i-1的微分变换，则机器人相邻两连杆之间的实际齐次坐标变换即ai+aiδai，那么机器人末端坐标系相对于基坐标系的实际齐次变换矩阵tr为：

将上式展开，并略去高阶摄动项，化简后得到下式：

其中，δp＝[dpxdpydpz]^t是机器人位置误差矩阵，j为3×(4n+1)连杆参数的微分变换雅可比矩阵，δx＝[δαδaδθδdδβ]^t为(4n+1)×1连杆参数误差矩阵；

(3)建立基于平面约束的机器人连杆参数误差模型

0为约束平面上第i个接触点的名义位置值，可通过机器人正运动学直接计算，ji为该位置处的雅克比矩阵，可通过关节角度值计算得到，实际位置pi^r＝piⁿ+jiδx，则相邻两接触点间的偏差向量：

其中，δji＝ji-ji-1；

同样地，那么由相邻的两个偏差向量可构建一垂直于平面的名义法向量：

同样地，那么：

(4)定位约束平面

对每个相机进行张正友内参标定及手眼标定，通过双目视觉获取约束平面在左右相机中的图像并提取单幅图像中的目标点信息，通过立体匹配即可定位约束平面在机器人基坐标系下的三维位置信息；

(5)驱动机器人对约束平面进行测量

将立体匹配后得到的约束平面位置值输入到机器人控制系统，驱动机器人对约束平面进行接触式测量，当测量头输出有接触信号时，立即记录当前各关节角度值，并对下一个约束点进行测量，若采集n+3个点：n0,n1,…,nn+2，则有：

hδx+s＝0

其中，则可产生3n个方程；

(6)机器人连杆参数辨识

通过改进的最小二乘法，对机器人运动学参数误差进行辨识，如下：

δx＝-(h^th+μi)^-1h^ts

约束点的数量要满足3n≥4n+1。

本发明的有益效果是：本发明提供的一种基于视觉辅助定位的机器人自标定方法，成本低、精度高、测量效率高。通过附加双目视觉系统，自动获取约束平面位置，从而避免手动示教测量；可以通过编程手段实现约束点按一定规律有序排列，为研究约束点对标定结果的影响奠定基础；标定的精度完全取决于平面度，与双目视觉定位精度无关；对大理石平面的摆放要求，只需要满足在机器人工作空间内同时测头可安全接触平面，不需要让约束平面与基坐标系的某个轴垂直。

本发明的其他特征和优点将在随后的说明书中阐述，部分地从说明书中变得显而易见，或者通过实施本发明，并与其他方法比较后而了解。

附图说明

下面结合附图对本发明的具体实施方式作进一步说明。

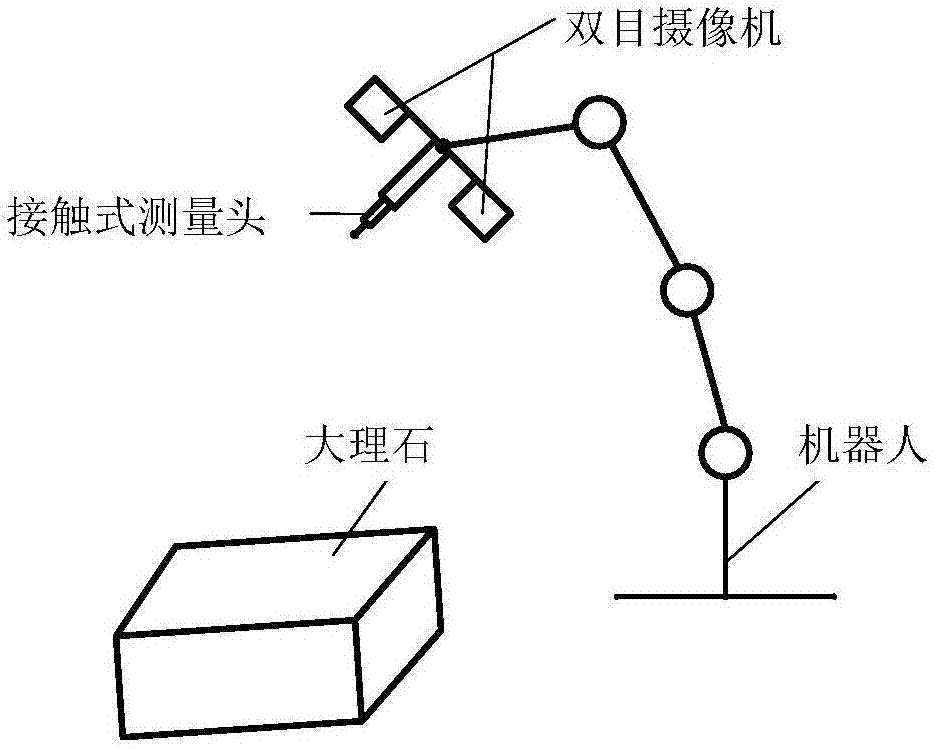
图1是标定现场简图；

图2是粘贴靶点后的平面示意图；

图3是基于视觉辅助定位的机器人自标定方法流程图。

具体实施方式

以下结合附图对本发明的优先实施例进行说明，应当理解，此处所描述的优选实施例仅用于说明和解释本发明，并不用于限定本发明。

参见附图1～3，本发明的基于视觉辅助定位的机器人自标定方法，包括以下几个步骤：

(1)建立机器人运动学模型

建立d-h法与md-h法相结合的机器人运动学模型，将坐标系i-1到坐标系i的变换过程描述为ai，ai＝f(αi-1,ai-1,di,θi,βi)，则机器人末端坐标系n相对于基坐标系的位姿矩阵⁰tn为：

⁰tn＝a0·a1·...·an

(2)建立机器人末端位置误差模型

按照微分变换的思想对ai进行全微分，得到由连杆几何参数误差造成的相邻坐标系间的微分摄动齐次矩阵dai：

δai是关节坐标系i相对于坐标系i-1的微分变换，则机器人相邻两连杆之间的实际齐次坐标变换即ai+aiδai，那么机器人末端坐标系相对于基坐标系的实际齐次变换矩阵tr为：

将上式展开，并略去高阶摄动项，化简后得到下式：

其中，δp＝[dpxdpydpz]^t是机器人位置误差矩阵，j为3×(4n+1)连杆参数的微分变换雅可比矩阵，δx＝[δαδaδθδdδβ]^t为(4n+1)×1连杆参数误差矩阵；

(3)建立基于平面约束的机器人连杆参数误差模型

设为约束平面上第i个接触点的名义位置值，可通过机器人正运动学直接计算，ji为该位置处的雅克比矩阵，可通过关节角度值计算得到，实际位置pi^r＝piⁿ+jiδx，则相邻两接触点间的偏差向量：

其中，δji＝ji-ji-1；

同样地，那么由相邻的两个偏差向量可构建一垂直于平面的名义法向量：

同样地，那么：

(4)定位约束平面

对左右两个相机分别进行张正友内参标定，得到四参数内参矩阵：

其中，fxi,fyi(i＝1,2)分别是x方向和y方向的尺度因子，[ui0,yi0](i＝1,2)分别是左右两相机的主点坐标；

对左右两个相机分别进行手眼标定，即确定摄像机坐标系相对于机器人末端法兰坐标系的齐次转换矩阵，利用传统手眼标定方法ax＝xb，至少使机器人运动到三个不同的姿态，分别计算获得左右两个相机的手眼矩阵x1,x2；

建立世界坐标系使之与机器人末端法兰坐标系重合，并令且

设目标点在末端法兰坐标系(世界坐标系)中的三维位置坐标为p＝[xwywzw]^t，可建立三维定位模型，如下：

zl,zr分别是目标点在摄像机坐标系下的深度信息，联立以上两个方程，可得：

其中，[ulvl]^t,[urvr]^t分别是目标点在左右两像素坐标系中的位置值，由此，可计算得到[xwywzw]^t，即通过立体匹配定位约束平面在机器人基坐标系下的三维位置信息；

(5)驱动机器人对约束平面进行测量

将立体匹配后得到的约束平面位置值输入到机器人控制系统，驱动机器人对约束平面进行接触式测量，当测量头输出有接触信号时，立即记录当前各关节角度值，并对下一个约束点进行测量，若采集n+3个点：n0,n1,…,nn+2，则有：

hδx+s＝0

其中，则可产生3n个方程；

(7)机器人连杆参数辨识

通过改进的最小二乘法，对机器人运动学参数误差进行辨识，如下：

δx＝-(h^th+μi)^-1h^ts

约束点的数量要满足3n≥4n+1。

由此，可辨识出机器人所有的连杆参数误差。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。