一种关节型机械臂逆运动学数值唯一解求取方法与流程

本发明属于现代智能制造技术领域，涉及工业机器人领域一种肩关节朝前偏置的关节型六自由度机械臂的逆运动学数值唯一解求解方法。

背景技术：

关节型机械臂的逆向运动学问题是在给定机械臂末端执行器坐标系相对于基坐标系的位置和姿态，以及所有机械臂关节几何参数的情况下，求取所有机械臂关节转动的角度值，是正向运动学的逆过程。正向运动学根据机械臂的结构几何参数可以得到前后相邻关节坐标系之间的齐次坐标变换矩阵t，也即两关节之间的位姿矩阵；若已知每个关节转动角度θ,通过将各关节齐次变换矩阵t依次连续右乘即可得到机械臂末端执行器坐标系的位姿矩阵，所得结果唯一。而逆向运动学的求解则相对复杂，且可能具有无解或多解情况，比如末端执行器坐标系在奇异点处无解，而反三角函数的周期性导致机械臂关节旋转角度解析解理论上的多解问题。

大多数关节型六自由度机械臂的腕部都是满足pieper准则的，即腕部相邻的三个关节旋转轴相交于一点，则腕部相邻的三个关节是解耦的。目前，机器人领域通用的坐标系建模方法多是denavit-hartenberg参数法,简称dh参数法，即一种为机械臂关节链中的每一个杆件建立坐标系的矩阵方法，该方法描述了相邻关节之间的坐标方向和几何参数，直观明了。例如，陶茂生等人公开的“用于六自由度的工业机器人的逆运动学求解方法”，专利号cn105573143a，需要根据求出的六个关节旋转轴转动角度对应的八组结果，解离上一关节空间所处位置对应的各个关节旋转轴角度差值范数总和最小的解。但是所求范数未能再次带入计算，只是作为在众多逆解中选择较优解的判断依据，其计算精度与计算速度不能满足现代生产的要求。朱齐丹等人公开的“一类六自由度机械臂运动学逆解的快速简便求法”，专利号cn103942427a，采用欧拉角变换矩阵进行求解，没有避免该方法的万向节锁问题。此外，田国会等人公开的“智能空间下的服务机器人逆运动学求解方法和装置”，以及吕亚辉等公开的“一种基于粒子群优化算法的机器人逆运动学求解方法”，采用了遗传算法和粒子群算法等智能算法进行逆运动学求解，程序复杂需要高性能的计算配置，且存在稳定性不足的问题。

技术实现要素：

本发明目的是针对现有机械臂的逆运动学求解存在的缺陷及不足：通用求解方法坐标系建模方法单一，求解过程复杂难懂，存在多解，且计算时间长求解速度慢。发明一种关节型机械臂逆运动学数值唯一解的求取方法，用于快速获取肩关节朝前偏置的关节型六自由度机械臂的唯一逆运动学解。方法按照改进的dh参数法建立机械臂关节坐标系,确定机械臂相邻关节之间的4个结构几何参数，计算相邻两坐标系的齐次坐标变换矩阵，并将齐次坐标变换矩阵依次右乘，得到末端坐标系o6对于基坐标系的位姿矩阵；整理位姿矩阵得到各关节转角θi、rpy转角rx,ry,rz和平移距离px,py,pz之间的关系式。再将关系式分别对关节转角θi求偏导数，得到6×6的雅可比矩阵j。最后，对于给定的末端坐标系o6的位姿矩阵，本方法采用一种改进的牛顿迭代法迭代法——levenberg-marquardt迭代算法，利用雅可比矩阵j计算关节坐标系逆运动学解，求得一组对应于位姿矩阵的满足精度要求的六个关节旋转角度值θi，克服了传统牛顿迭代法对雅可比矩阵j必须满秩的要求。本方法行之有效，过程简单明了。

本发明采用的技术方案是一种关节型机械臂逆运动学数值唯一解的求取方法，该方法按照改进的dh参数法建立机械臂关节坐标系,确定机械臂相邻关节之间的4个结构几何参数，计算相邻两坐标系的齐次坐标变换矩阵，并将齐次坐标变换矩阵依次右乘，得到末端坐标系o6对于基坐标系的位姿矩阵；整理位姿矩阵得到各关节转角θi,i＝1,2,3,4,5,6与rpy转角rx,ry,rz和平移距离px,py,pz之间的关系式；再将关系式分别对关节转角θi求偏导数，得到6×6的雅可比矩阵j；最后，对于给定的末端坐标系o6的位姿矩阵，采用一种改进的牛顿迭代法—levenberg-marquardt迭代算法，利用雅可比矩阵j计算关节坐标系逆运动学解，求得一组对应于位姿矩阵的满足精度要求的六个关节旋转角度值θi；方法的具体步骤如下：

步骤一，构建关节型机械臂及坐标系。

关节型机械臂由基座a、末端执行器g、5个连杆b、c、d、e、f和6个旋转关节1、2、3、4、5、6组成；基于改进的dh参数法建立机械臂各关节坐标系，坐标系包括：基坐标系o0，机械臂六个旋转关节对应坐标系o1～o6以及机械臂末端执行器的坐标系o6；各关节坐标系具体为：关节i的zi轴与关节i的轴线在同一直线上，而xi轴则在关节i和i+1轴线的公共法线上，其方向从i指向i+1；当两关节轴线相交时，xi-1的方向与两矢量的叉积zi-1×zi同轴、同向或反向，xi-1的方向总是沿着公共法线从轴i-1指向轴i；当两轴xi-1和xi平行且同向时，第i个转动关节的θi为零；yi轴由右手直角坐标系规则确定，其中，i＝1,2,3,4,5,6；将第一个关节坐标系的初始位置设置在机械臂的基座上与基坐标系{o0:x0,y0,z0}重合，基坐标系始终保持不变。

步骤二，建立机械臂关节相邻坐标系的齐次坐标变换矩阵。

根据机械臂相邻关节之间的4个结构几何参数：连杆夹角θi、连杆扭角αi、连杆长度ai、连杆距离di计算相邻坐标系的齐次坐标变换矩阵^i-1ti,i＝1,2,...6；各几何参数的定义：相邻关节i和i+1之间的连杆转角θi为xi轴与xi-1轴之间的夹角，绕zi轴从xi-1轴到xi轴，符合右手规则时为正，对于转动关节，θi为变量；连杆扭角αi为zi轴与zi+1轴之间的夹角，绕xi轴从zi轴到zi+1轴，符合右手规则时为正，当两关节轴线平行时，αi＝0，当两关节轴线垂直时，αi＝-90°或90°；连杆长度ai为zi轴与zi+1轴的公垂线长度，沿xi轴方向测量，当两关节轴线平行时，ai＝li，li为连杆的长度，当两关节轴线垂直时，ai＝0；相邻关节之间的连杆距离di为xi轴与xi-1轴之间的距离，在zi轴上测量，对于转动关节，di为常数。

按照关节坐标系之间的齐次变换规则计算出相邻坐标系的各齐次变换矩阵^i-1ti；机械臂的相邻关节坐标系间的齐次坐标变换矩阵^i-1ti为：

其中，θi为连杆夹角、αi为连杆扭角、ai为连杆长度、di为连杆距离。

步骤三，建立机械臂逆运动学求解的齐次坐标变换矩阵。

将机械臂关节相邻坐标系的各齐次变换矩阵^i-1ti依次右乘得到：

其中，等式右边矩阵：⁰t1、¹t2、²t3、³t4、⁴t5、⁵t6分别为第一、第二、第三、第四、第五、末端坐标系相对于前一坐标系的齐次坐标变换矩阵。

等式左边矩阵⁰t6为末端坐标系o6相对于基坐标系o0的齐次坐标变换矩阵；其中，nx,ny,nz分别为末端坐标系{o6:x6,y6,z6}的x6轴与基坐标系的x0,y0,z0轴的夹角余弦值；ox,oy,oz分别为末端坐标系的y6轴与基坐标系的x0,y0,z0轴的夹角余弦值；ax,ay,az分别为末端坐标系的z6轴与基坐标系的x0,y0,z0轴的夹角余弦值；px,py,pz为末端坐标系原点o6在基坐标系中的笛卡尔坐标。

⁰t6还可以用rpy组合变换表示：

其中，分别是的简写，trans(px,py,pz)代表末端坐标系沿着基坐标系的x,y,z轴平移px,py,pz距离；表示末端坐标系先绕着基坐标系z轴旋转角，再绕新的y轴旋转θ角，再绕新的z轴旋转φ角，即rpy转角rx,ry,rz。

联立公式(2)和(3)，得到各关节转角θi(i＝1,2,3,4,5,6)、rpy转角rx,ry,rz和平移距离px,py,pz之间的关系式：

步骤四，建立机械臂逆运动学求解的雅可比矩阵。

根据公式(4)中的rx,ry,rz,px,py,pz与θi,i＝1,2,3,4,5,6之间的关系式，将fi,i＝1,2,3,4,5,6分别对θi,i＝1,2,3,4,5,6求偏导数得到关节坐标系的雅可比矩阵：

步骤五，关节型机械臂逆运动学数学唯一解求取。

对于给定的机械臂末端坐标系o6的位姿矩阵，使用经典牛顿迭代算法，计算关节坐标系逆运动学数值解时，由于雅可比矩阵j是与关节转角θi有关的矩阵，在某些特殊的情况下，j^tj是奇异的，此时牛顿迭代法无解。所以，求解关节坐标系逆运动学数值解时，采用一种改进的牛顿迭代法迭代法——levenberg-marquardt迭代算法，lm迭代法克服了牛顿迭代法对雅可比矩阵j必须满秩的要求。

当使用lm迭代法计算给定的机械臂末端坐标系o6的位姿矩阵tend对应的逆运动学数值解θend时，记录下当前末端坐标系o6的位姿矩阵tcur以及对应的各关节转角θcur。由tend和tcur计算微分算子δ：

由微分算子δ可以得到微分运动向量d＝[dxdydzδxδyδz]^t。

对于当前迭代点θcur，lm迭代法的搜索方向为：

dθ＝(j^tj+μi)^-1j^td(7)

其中，μ为正参数，是为了防止当j^tj接近奇异时dθ过大。将θcur与dθ相加得到新的迭代点θnew，再利用正运动学模型计算新的迭代点对应的机械臂末端坐标系位姿矩阵tnew，将其带入公式(5)和公式(6)，更新雅可比矩阵jnew和微分运动向量dnew。

为保证lm迭代法全局收敛，在每一次迭代后比较dnew和d的二范数。若||dnew||2<||d||2，则令将μnew,dnew,jnew带入下一次迭代。若||dnew||2≥||d||2，则令μnew＝2μ，将μnew,d,j带入下一次迭代。直到||dnew||2小于迭代精度时，结束迭代过程；此时，θnew即为关节坐标系逆运动学数值解。

本发明的有益效果是该方法采用levenberg-marquardt迭代算法快速求取肩关节朝前偏置的关节型六自由度机械臂的唯一逆运动学解，克服了传统牛顿迭代法对雅可比矩阵j必须满秩的要求，对该类构型的机械臂，坐标系建模方法简单，并且数值解精度高。本发明中提出的逆运动学求解过程更加行之有效，具有求解精度高、求解速度快、求解过程更加简单易行的特点。

附图说明

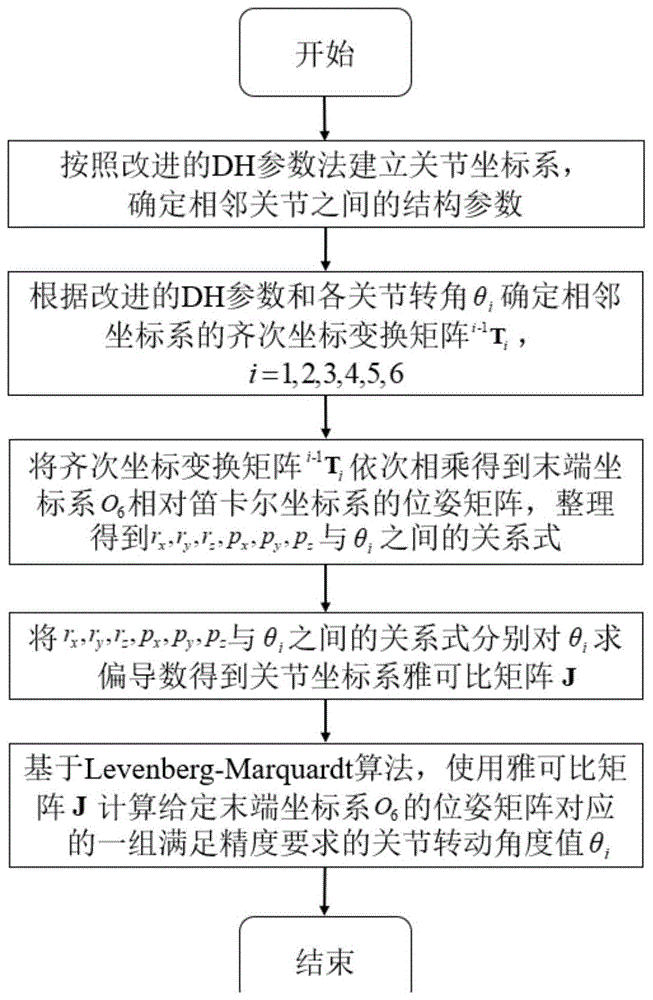
附图1—关节型机械臂逆运动学数值唯一解的求取方法流程图。

附图2—关节型六自由度机械臂的结构图。其中，a-基座，b-连杆1，c-连杆2，d-连杆3，e-连杆4，f-连杆5，g-末端执行器，a2-连杆2的长度，a3-连杆3的长度，a4-连杆4的长度，d4-连杆3与连杆4的距离，d6-连杆5与末端执行器之间的距离。

附图3—关节型六自由度机械臂的结构简图及各关节坐标系。其中，1-关节1，2-关节2，3-关节3，4-关节4，5-关节5，6-关节6；各坐标系的确定方法采取改进的dh参数法，各关节均绕着该关节坐标系的z轴旋转，具体的，zi轴沿第i+1关节的轴线，xi沿zi轴和zi-1轴的公垂线，指向背离zi-1轴的方向，yi轴由右手直角坐标系规则确定，oi为第i个坐标系的原点；实施例将第一个关节坐标系的初始位置设置在机械臂的基座上与基坐标系{o0:x0,y0,z0}重合，基坐标系始终保持不变。

具体实施方式

下面结合附图和技术方案详细叙述本发明的具体实施方式。

附图1为本发明关节型机械臂逆运动学数值唯一解的求取方法流程图；附图2为关节型六自由度机械臂结构图，机械臂由基座a、末端执行器g、5个连杆b、c、d、e、f和6个旋转关节1、2、3、4、5、6组成。机械臂各关节坐标系如附图3所示，方法流程的具体步骤如下：

步骤一,基于改进的dh参数法，建立机械臂各关节坐标系,如附图3所示。

步骤二，给定初始机械臂相邻关节之间的4个结构几何参数：连杆转角θi、连杆扭角αi、连杆长度ai、连杆距离di。本实施例中，机械臂各连杆的dh参数为：i＝1时，连杆转角为θ1，连杆距离为0，连杆长度为0，连杆扭角为0；i＝2时，连杆转角为θ2+90°，连杆距离为0，连杆长度为a2，连杆扭角为90°；i＝3时，连杆转角为θ3，连杆距离为0，连杆长度为a3，连杆扭角为0；i＝4时，连杆转角为θ4，连杆距离为d4，连杆长度为a4，连杆扭角为90°；i＝5时，连杆转角为θ5，连杆距离为0，连杆长度为0，连杆扭角为-90°；i＝6时，连杆转角为θ6+90°，连杆距离为d6，连杆长度为0，连杆扭角为90°。在本实施例中，d6包含工具长度。

基于改进的dh参数法，求出实施例中各结构的参数值如下：

a2＝160,a3＝790,a4＝155,d4＝795,d6＝145

计算机械臂关节相邻坐标系的齐次坐标变换矩阵^i-1ti,i＝1,2,...6；利用公式(1)机械臂的相邻关节坐标系间的齐次坐标变换矩阵^i-1ti，本实施例中各变换矩阵如下：

步骤三，将公式(2)与(3)联立得到各关节转角θi,i＝1,2,3,4,5,6与rpy转角rx,ry,rz和平移距离px,py,pz之间的关系式(4)。

步骤四，根据机械臂的实际工作范围，本实施例给定一组关节转角θ1＝30°,θ2＝-20°,θ3＝40°,θ4＝-40°,θ5＝20°,θ6＝50°通过正运动学计算得到末端坐标系相对于基坐标系的位姿矩阵tend，

令当前末端坐标系o6的位姿矩阵tcur，

以及对应的各关节转角θcur＝[000000]^t。通过公式(5)计算此时迭代点θcur对应的雅可比矩阵j，

步骤五，设正参数μ＝0.1，将μ,j,tcur,θcur,tend带入lm迭代算法，得到机械臂关节坐标系逆运动学数值解θend，

θ1＝30.000000000007°,θ2＝-19.999999999997°,θ3＝39.999999999986°,θ4＝-39.999999999747°,θ5＝20.000000000004°,θ6＝49.999999999744°

由此得到唯一的一组机械臂关节旋转角度表达式，计算结果误差小于1×10^-7°，利用已确定的表达式再进行几组正逆运算，结果同样满足误差小于1×10^-7°的结论。

本发明对于关节型六自由度机械臂逆运动学数值唯一解求取方法，对此类构型的机械臂关节坐标系建模方法简单易行，能够迅速获得唯一解，并且结果误差小于1×10^-7°。