一种机器人零位和工具坐标标定方法与流程

本发明涉及机器人控制领域，尤其涉及机器人零位和工具坐标标定方法。

背景技术：

机器人是一种开环的运动学结构，通过角度测量装置(通常是增量式码盘)得到关节转动的角度值，通过机器人运动学模型得到当前机器人末端执行器的空间位姿。由于在机器人生产过程中机械制造与装配、编码器、运动控制等环节均不可避免地存在各种误差，在机器人的使用过程中的重力形变、热变形、间隙和磨损以及其他随机误差等，因此机器人末端的实际空间位姿与理想值相比通常存在较大偏差，从而影响机器人的运动精度。通过对机器人进行标定，获取机器人准确的结构与位姿参数，可以将机器人的位姿误差大幅度降低，进而将机器人的绝对精度提高到重复精度的水平。

机器人在实际应用过程中，由于关节零位和工具坐标不够精确，导致机器人末端走直线轨迹和圆弧轨迹时路径偏差较大，影响实际应用的效果。现有的标定方法，在测量设备上需要高精密设备，比如激光跟踪仪。这种设备价格昂贵，操作复杂，机器人精度标定成本较高。需要一种标定算法快速实现机器人关节零位和工具坐标的标定，得到实际机器人关节零位和理论关节零位之间的误差，将误差补偿到控制器中，提高机器人的精度。

技术实现要素：

本发明的主要目的在于提供一种高效便捷的机器人零位和工具坐标标定方法，解决了现有标定过程中采用高精度设备成本高，操作复杂的缺点，依靠软件算法提高了机器人精度。

本发明采用的技术方案如下：一种机器人零位和工具坐标标定方法，包括如下步骤：

步骤一：对关节角数据进行记录测量；

步骤二：对机器人的正运动学进行分析：

步骤三：建立机器人关节零位和工具坐标的误差模型；

步骤四：对误差模型进行计算；

步骤五：更新误差模型；

步骤六：计算位置误差；

步骤七：补偿误差。

所述步骤一具体做法为：分别在机器人末端法兰和机器人工作区域一固定点安装测量针尖；保持两个测量尖点始终相对，变换机器人姿态，读取机器人关节角度数据。

所述步骤三的具体步骤为：建立机器人关节零位和工具坐标的误差模型：δ＝[δq2，δq3，δq4，δq5，δpx，δpy，δpz]，在不改变机器人零位和工具安装位置的情况下，误差δ为常量；

所述步骤四的具体步骤为：据机器人正运动学算法，机器人工具末端的位置和机器人关节角q＝[q1，q2，q3，q4，q5，q6]和工具坐标tool＝[px，py，pz]的关系为p＝f(q，tool)；测量的实际位置和名义位置的误差p^c-pⁿ＝j*δ，则实际位置p^c＝pⁿ+j*δ，其中j为雅可比矩阵；

所述步骤五的具体步骤为：取两次测量结果，由于针尖始终相对，认为两次测量的实际位置相同，则由此可得和可以由公式p＝f(q，tool)得到；利用测量n＝20次的关节数据构造末端名义位置误差模型：其中由最小二乘法得到误差δ＝(b^t*b)^-1*b^t*y；

所述步骤七的具体步骤为：将误差补偿到机器人关节和工具坐标后，计算δp是否满足误差要求，如果满足，则误差得到；如果不满足，重复步操作，操作步骤迭代计算；将步骤计算的关节零位误差补偿到控制器中，提高机器人的精度。

本发明的有益效果为：本发明解决了现有标定过程中采用高精度设备成本高，操作复杂的缺点，依靠软件算法提高了机器人精度。本发明根据机器人末端点位误差计算出关节零位误差和工具坐标误差，测量设备简单，成本低，可广泛与用于中小企业。本发明系统整体结构设计合理，整个系统体积小、重量轻、高度集成，且通过控制器整体控制，使用简单方便、对机器人本体性能没有影响，既可以适合新机器人设计、又可以满足在役机器人需要。

附图说明

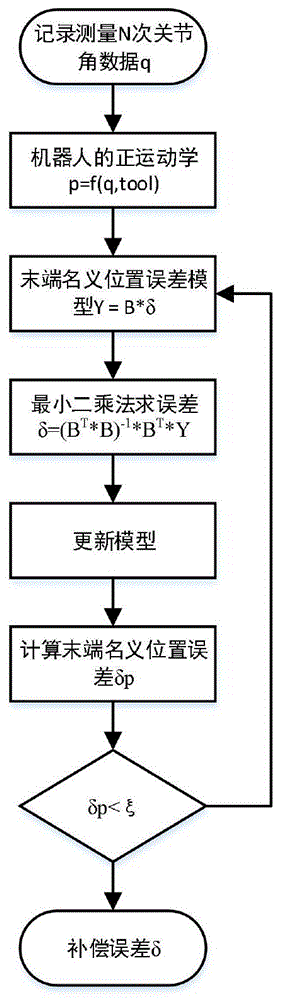
图1为本发明流程示意图。

图2为本发明标定示意图。

具体实施方式

实施例1

本发明采用的技术方案如下：一种机器人零位和工具坐标标定方法，包括如下步骤：

步骤一：对关节角数据进行记录测量；

步骤二：对机器人的正运动学进行分析：

步骤三：建立机器人关节零位和工具坐标的误差模型；

步骤四：对误差模型进行计算；

步骤五：更新误差模型；

步骤六：计算位置误差；

步骤七：补偿误差。

实施例2

一种机器人零位和工具坐标标定方法，包括如下步骤：

1)分别在机器人末端法兰和机器人工作区域一固定点安装测量针尖。

2)保持两个测量尖点始终相对，变换机器人姿态，读取机器人关节角度数据。

3)建立机器人关节零位和工具坐标的误差模型

δ＝[δq2，δq3，δq4，δq5，δpx，δpy，δpz]，在不改变机器人零位和工具安装位置的情况下，误差δ为常量。

4)根据机器人正运动学算法，机器人工具末端的位置和机器人关节角q＝[q1，q2，q3，q4，q5，q6]和工具坐标tool＝[px，py，pz]的关系为p＝f(q，tool)。

5)测量的实际位置和名义位置的误差p^c-pⁿ＝j*δ，则实际位置p^c＝pⁿ+j*δ，其中j为雅可比矩阵。

6)取两次测量结果.由于针尖始终相对.认为两次测量的实际位置相同，则由此可得和可以由公式p＝f(q，tool)得到。

7)利用测量n＝20次的关节数据构造末端名义位置误差模型：

其中

8)由最小二乘法得到误差δ＝(b^t*b)^-1*b^t*y。

9)将误差补偿到机器人关节和工具坐标后，计算δp是否满足误差要求，如果满足，则误差得到；如果不满足，重复步骤8，步骤9迭代计算。

10)将步骤9计算的关节零位误差补偿到控制器中，提高机器人的精度。

以上显示和描述了本发明的基本原理和主要特征和本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。