一种使用机械臂完成不可重复覆盖任务抬起次数最少的方法与流程

本发明涉及机械臂路径规划技术领域，具体地说，是一种使用机械臂完成不可重复覆盖任务抬起次数最少的方法。

背景技术：

物体表面的覆盖任务是工业应用中的常见任务，被广泛应用于物体表面的近距离建模、喷漆、抛光等工作中。为了满足对三维空间中一般形状的物体进行加工的需求，覆盖任务通常由机械臂完成。

一方面，机械臂的运动学问题是几十年来一直被研究的热门问题。机械臂运动学的实质是寻找机械臂的各个关节角度组成的关节空间到机械臂的末端执行器的位姿空间的映射。当机械臂中具有旋转关节时，这种映射关系是非线性的。另一方面，曲面的覆盖问题是机器人路径规划任务中的覆盖路径规划问题，针对给定的待覆盖空间，设计出一条路径，使得机器人沿着路径运行后可以经过待覆盖空间上的每一个点，在此过程中机器人视作一个质点。

在物体表面的覆盖问题中，机械臂末端安装的末端执行器沿着设定好的覆盖路径运行，即可经过物体表面的每一个点。然而，由于机械臂存在运动学约束，它不能使得末端执行器完整跟踪整条覆盖路径。在这种情况下，覆盖工作被迫中断，且机械臂需要调整其姿态来完成后续的跟踪任务。传统的覆盖路径规划算法是在被覆盖区域上进行路径生成的算法，在机械臂的覆盖路径规划问题中相当于在物体表面直接生成覆盖路径。然而由于机械臂的正运动学是非线性的，工作空间中的覆盖路径很容易因为机械臂的运动学约束而被截断。机械臂需要将末端执行器抬起，在空中完成机械臂位姿的变换，再重新接触。末端执行器的“脱离-重新接触”的过程需要复杂的控制策略，浪费额外的时间和能量，降低工业生产效率。

技术实现要素：

为了克服现有技术的不足，本发明的目的在于提供一种使用机械臂完成不可重复覆盖任务抬起次数最少的方法，在完全已知环境下、对物体表面进行覆盖任务的方法。该方法在整个覆盖任务执行过程中，机械臂的末端执行器只需要与物体表面解除接触最少次数。

本发明的目的是通过以下技术方案来实现的：

一种使用机械臂完成不可重复覆盖任务抬起次数最少的方法，所述机械臂的末端执行器与待覆盖物体表面间的接触为点接触，且待覆盖物体、机械臂以及环境中的障碍物的相对位置关系已知，且在覆盖任务执行过程中保持不变。

所述使用机械臂完成不可重复覆盖任务抬起次数最少的方法具体包括以下步骤：

步骤一、对待覆盖物体的曲面m上所有的点进行机械臂逆运动学求解，获得覆盖此点时机械臂的位姿，对于曲面m上的任一点p，所有的可行位姿记为{jp1，jp2，…，jpn}，若待覆盖物体表面被完整覆盖，则所有的点均对应一组可行的位姿；否则，待覆盖物体表面上不能覆盖到的点没有对应的位姿。曲面m上的所有点的可行位姿构成机械臂的关节空间，所述机械臂的关节空间包括奇异位姿和非奇异位姿。

步骤二、除去所有奇异位姿后，所述机械臂的关节空间被分割成若干不相交的集合，每个集合中存储能被机械臂连续执行的位姿，将相同集合中的位姿标注相同的编号，不同集合中的位姿标注不同的编号，将不同的集合编号设置为c1，…，cn，曲面m上的每一点根据其可行位姿对应的编号获得点p对应的编号组合。

步骤三、根据待覆盖物体的曲面m上的点的连通性，把具有相同编号组合、且在待覆盖物体的曲面m上连通的点划分为同一个胞腔。两个胞腔之间的交界处记为一条拓扑边。每个胞腔具有唯一的编号，记为第一胞腔、第二胞腔……、第n胞腔，且在后文被称为第一胞腔、第二胞腔等。每个胞腔可覆盖此胞腔的不同种机械臂位姿(即前述的编号组合)，还按顺序存储与之邻接的胞腔的编号。

步骤四、对于单连通的胞腔，用二进制数编码其所有不同的切割方式：二进制数的数字个数就是此胞腔的拓扑边个数。根据二进制数中对应数位是1还是0，0表示这条拓扑边会被保留，即拓扑边两侧的两个胞腔最终会是不同的编号，在机械臂执行时末端执行器抬起一次；1表示这条拓扑边会被删除，即拓扑边两侧的区域最终是相同的编号，在机械臂执行时被末端执行器连续、无抬起地覆盖。对于拓扑边数为1、2、3的胞腔，直接使用枚举方法获得最优解。然而，对于拓扑边数超过3的胞腔，经过分解后可能形成子胞腔，而子胞腔的拓扑边数少于原胞腔，通过递归求解出所有出现的子胞腔，获得所有可能的解。

步骤五、对于n连通胞腔，n连通胞腔内部有n-1个内部边界。我们使用递归的方法求解n连通胞腔。n连通胞腔的分解方法步骤如下：

(5.1)当n＝1时，所述胞腔即为步骤四中的单连通胞腔，使用步骤四求解即可。

(5.2)当n＝2时，所述胞腔有两条边界，记为内边界和外边界。每条边界都由若干拓扑边组成，其中每个拓扑边都会连接至另一个胞腔。我们使用如下方法将二连通胞腔的所有可能解法进行完整的分类：

(5.2.1)考虑不存在内外边界相连通的切割路径的情况，将内外边界分开，视作两个单连通胞腔各自求解；

(5.2.2)考虑内外边界相连通的切割路径，先设计两条连接内、外边界的切割路径，将二连通胞腔的分解问题转化为两个单连通胞腔的分解问题，而后使用步骤四中单连通胞腔的求解方法进行求解。

(5.3)当n＞2时，将n连通胞腔的n-1个内边界编号，其中外边界和第i个内边界包含的拓扑边分别用如下符号表示：

ω＝(α1，…，αk)

其中，αk表示该胞腔与它的第k个外部邻接胞腔之间的拓扑边，表示该胞腔与它的第i个内部边界上编号为ji的胞腔之间的拓扑边。

(5.3.1)只考虑外边界ω和第一条内边界ω¹，根据步骤五中二连通胞腔的求解过程可知，由ω和ω¹构成的二连通胞腔中设计两条切割路径使之成为两个单连通胞腔。

(5.3.2)再将第二条内边界ω²放入(5.3.1)中生成的两个单连通子胞腔之一。则这个被放入了ω²的那个单连通子胞腔成为了一个二连通子胞腔。将该二连通子胞腔使用(5.2)所述步骤求解，最终将其再分为两个单连通子胞腔。经过此步骤后，原先的n连通胞腔包含了ω，ω¹，ω²，且已经被分为了三个单连通子胞腔。

(5.3.3)对于后续的每个内边界ω³，…，ω^n-1，均依次执行以下步骤：将ω³，…，ω^n-1放入已经生成好的某个单连通子胞腔中使之变为二连通胞腔，并再切分为两个单连通子胞腔。在放入第i个内边界时，原胞腔已经被分为了i份。将n-1个内边界都放入胞腔中后，原胞腔被切分为n个单连通子胞腔，将这n个单连通子胞腔通过步骤四进行求解。

步骤六、根据步骤四、五的求解过程，使用迭代方式求解待覆盖物体表面上机械臂的运动学模型生成的拓扑图：

(6.1)对待覆盖物体表面上的第一胞腔，遍历所述第一胞腔的所有可能的切割方法并设置编号，即完成所述第一胞腔的所有解法。对所有解法中的每一个，执行步骤(6.2)；

(6.2)对待覆盖物体表面上的第二胞腔，遍历所述第二胞腔的所有可能的切割方法并设置编号，即完成所述第二胞腔的所有解法。将第二胞腔的所有解法与第一胞腔设定有矛盾的解删掉。对第二胞腔中剩下的可行解法中的每一个，执行步骤(6.3)；

(6.3)依次对待覆盖物体表面上的第三胞腔至第n胞腔执行步骤(6.2)，使得每个胞腔都被设置切割方法，且每个切出的子胞腔均为唯一的编号，即获得机械臂覆盖子胞腔的方式。

进一步地，所述待覆盖物体表面的点只能被覆盖一次。

相比于现有技术，本发明的有益效果在于：本发明公开了一种使用机械臂完成不可重复覆盖任务抬起次数最少的方法，可以保证机械臂的末端执行器在覆盖任务执行过程中离开物体表面的次数最少。由于机械臂的力/力矩-位置切换控制策略公认是复杂的，且在末端执行器与物体表面不接触时机械臂的运动不会导致物体的任何区域被覆盖，在机械臂覆盖任务中将末端执行器抬起额外的、非最少的次数会造成大量的时间、能量损失。本发明旨在提高在工业应用中机械臂完成覆盖任务的效率，其直接应用场景包括物体表面的近距离建模、喷漆、抛光等工作。

首先，本发明方法对机械臂选择的限制仅为非冗余。非冗余机械臂的工作意味着可以最大化机械臂的效率。现有工业应用中由于缺少本发明提供的最小化抬起次数的覆盖路径设计方法，若选择非冗余机械臂，则末端执行器需要频繁抬起，极大地降低了工作效率。因此现有的工业应用中的相同问题的解决方案仅是使用冗余机械臂，例如，任务本可以使用五自由度机械臂完成，但因抬起次数过多，效率太低，只能使用六自由度或七自由度机械臂完成相同工作，或使用多机械臂，例如，两个五自由度机械臂。因此，本发明具有实际的工业应用价值。

其次，本发明只要求机械臂、待覆盖物体和周围障碍物的相对位置关系在覆盖任务执行过程中是不变的，而对他们的实际空间位置没有约束，可以是不固定的。例如，被工业流水线承载的待覆盖物体停在固定的机械臂前，由机械臂完成其表面的覆盖任务后再继续移动。又例如，移动机械臂平台(机械臂安装在可移动的底盘平台上)移动至待覆盖物体周围的某处，并使用传感器感知了周围环境后，执行覆盖任务，而在机械臂完成覆盖任务的过程中底盘不移动。综上，本发明在实际工业应用中具有广泛的应用场景。

本方法使用枚举的方法遍历编号({c1，…，cn})的所有可能组合，因此可以求解出在给定机械臂构型、物体模型、障碍物模型及它们之间的相对位置关系情况下，机械臂使用最少抬起次数完成覆盖任务的所有最优解。可以证明，任何一种满足最少抬起次数的机械臂覆盖方案都是本方法给出的某个最优解的同胚变形。(同胚变形是指将不同的区域之间的边界连续地变化成其它形状或连续地挪至其它位置，不改变每个区域的连通性。)

因此，本发明的方法具有使得机械臂的末端执行器抬起次数最少的特点。又考虑到在末端执行器抬离物体表面的过程中，机械臂的运动不会覆盖物体表面的任何区域，所以，本发明的方法间接地最小化了机械臂在覆盖任务中的能量损耗。

附图说明

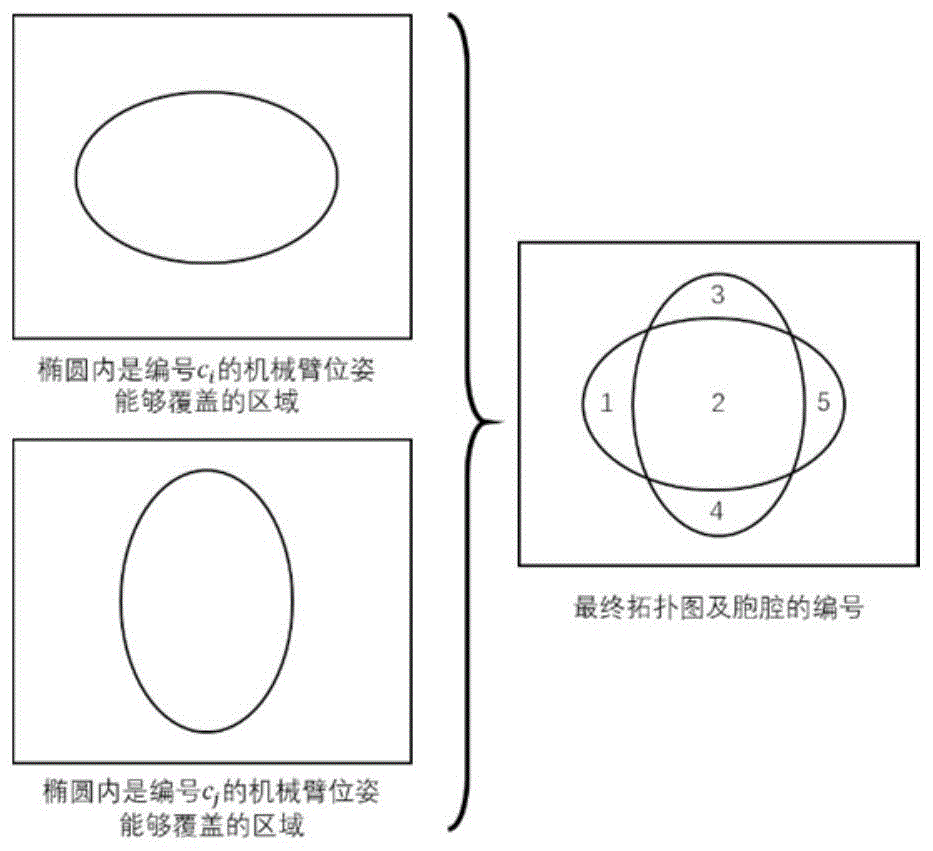
图1是拓扑图的建立过程的示意图；

图2是对单连通胞腔进行分解时，三类等价的区域分解方法；

图3是对具有三条拓扑边的单连通胞腔进行分解时的所有可能解法；

图4是对具有四条拓扑边的单连通胞腔进行分解时的所有可能解法，以及生成子胞腔的示意图；

图5是对二连通胞腔进行求解时，在内边界与外边界之间不存在切割路径连通的情况下，“直接求解二连通胞腔”和“先将内边界去掉，将外边界构成的单连通胞腔求解后，再将内边界放置于外边界中任意位置”这两种方法的等价性的示意图；

图6是二连通胞腔中内边界和外边界的等价性的示意图；

图7是二连通胞腔中的循环切割路径和非循环切割路径的示意图；

图8是二连通胞腔中循环切割路径和非循环切割路径的等价性的示意图；

图9是二连通胞腔中不连接内、外边界的切割路径可以看成是在已经切分为两个单连通子胞腔中再进行分解的切割路径的示意图；

图10是二连通胞腔中，多于两个的连接内、外边界的切割路径，可以看成是在已经切分为两个单连通子胞腔中再进行分解的切割路径的示意图；

图11是将n连通胞腔迭代地求解的流程示意图；

图12是在三连通胞腔中，在已经放入一个内边界并且完成切分的情况下，将第二个内边界放入胞腔中时，不将其放在已有的切割路径上的最优性示意图。

具体实施方式

本发明公开了一种使用机械臂完成不可重复覆盖任务抬起次数最少的方法。机械臂的末端执行器对每个区域都可以保证连续地完成覆盖，即，不需要解除末端执行器与物体表面的接触。本方法保证将物体表面只分解为最少块区域，进而保证了末端执行器在完成物体表面覆盖任务的过程中只需要抬起最少次数。

本发明使用非冗余机械臂完成覆盖任务，所述机械臂的末端执行器与待覆盖物体表面间的接触为点接触，且待覆盖物体、机械臂以及环境中的障碍物的相对位置关系已知，且在覆盖任务执行过程中保持不变。点接触是灵活的，只要在规划具体覆盖路径时，该方法不考虑末端执行器与被覆盖物体表面的接触面积，即认为是点接触。所述待覆盖物体表面的点只能被覆盖一次。

所述使用机械臂完成不可重复覆盖任务抬起次数最少的方法具体包括以下步骤：

步骤一、对待覆盖物体的曲面m上所有的点进行机械臂逆运动学求解，获得覆盖此点时机械臂的位姿，对于曲面m上的任一点p，所有的可行位姿记为{jp1，jp2，…，jpn}，若待覆盖物体表面被完整覆盖，则所有的点均对应一组可行的位姿；否则，待覆盖物体表面上不能覆盖到的点没有对应的位姿。曲面m上的所有点的可行位姿构成机械臂的关节空间，所述机械臂的关节空间包括奇异位姿和非奇异位姿。

步骤二、因为机械臂处于奇异位姿时，机械臂的雅克比矩阵不满秩，使得机械臂的末端执行器不能抵抗来自某个方向的力或力矩，所以在末端执行器与待覆盖物体有力接触的任务中，奇异位姿都是不能被使用的，除去所有奇异位姿后，所述机械臂的关节空间被分割成若干不相交的集合，每个集合中存储能被机械臂连续执行的位姿，将相同集合中的位姿标注相同的编号，不同集合中的位姿标注不同的编号，将不同的集合编号设置为c1，…，cn，曲面m上的每一点根据其可行位姿对应的编号获得点p对应的编号组合。

步骤三、如图1所示，根据待覆盖物体的曲面m上的点的连通性，把具有相同编号组合、且在待覆盖物体的曲面m上连通的点划分为同一个胞腔。两个胞腔之间的交界处记为一条拓扑边。每个胞腔具有唯一的编号，记为第一胞腔、第二胞腔……、第n胞腔。每个胞腔可覆盖此胞腔的不同种机械臂位姿，还按顺序存储与之邻接的胞腔的编号。

步骤四、对于单连通的胞腔，给出三个等价关系，将胞腔进行分解的方法，具有相同的抬起次数。对于任意两种等价的将胞腔进行分解的方法，只需要考虑其中一个分解方法，而一个分解方法因为具有相同的抬起次数，并不会更少，所以不会导致这个分解方法失去最优性。显然，对物体表面的某个单连通区域进行划分的方法有无穷多种，通过给出的三个等价关系排除大多数分解方法，最终使得需要考虑的不等价的分解方法只有有限多个。如图2所示，在图2中虚线表示的是拓扑边，设计切割路径使得胞腔被分成多个部分，其中可以发现：(1)将拓扑边的任何非端点处设置为切割路径的起点或终点是没有意义的，因为可以将端点连续地移动至它所在的拓扑边的端点上，而不会增加抬起次数；(2)切割路径没有必要穿过其它拓扑边，因为它可能会导致不必要的额外抬起次数；(3)切割路径之间没有必要交叉，因为这种切割方式等价于将胞腔沿着拓扑边切割，而不会增加抬起次数。对于某一个胞腔，用二进制数编码其所有不同的切割方式：二进制数的数字个数就是此胞腔的拓扑边个数。根据二进制数中对应数位是1还是0，0表示这条拓扑边会被保留，即拓扑边两侧的两个胞腔最终会是不同的编号，在机械臂执行时末端执行器抬起一次；1表示这条拓扑边会被删除，即拓扑边两侧的区域最终是相同的编号，在机械臂执行时被末端执行器连续、无抬起地覆盖。图3和图4给出了具有三条拓扑边的胞腔和具有四条拓扑边的胞腔的所有不同的区域分解。在图3中，最左侧为由三条虚线作为边界的具有三条拓扑边的单连通胞腔的示意图，其存储的邻接胞腔的顺序为逆时针(左上、左下、右)。在图3右侧给出了使用二进制数表示的8种不同的切割方法，其中0表示对应的拓扑边在胞腔分解方法中是保持的，即从虚线变成实线，而1表示对应的拓扑边的两侧的胞腔是连在一起的，中间的拓扑边会被删除，即删除虚线。

对于拓扑边数为1、2、3的胞腔，直接使用枚举方法获得最优解。然而，对于拓扑边数超过3的胞腔，经过分解后可能形成子胞腔，此时，子胞腔的拓扑边仍然是待定的，例如图4中编码为xx11、x11x、1xx1、11xx这四种情形，4-胞腔被分解后生成了一个3-胞腔，这个子胞腔的一条边是指定的切割路径，另外两条边是待确定保留或者移除的拓扑边。注意到，因为生成的切割路径一定是保留的，所以对整个求解过程而言，生成子胞腔并不会导致问题求解具有更多的分支。而子胞腔的拓扑边数少于原胞腔，通过递归求解出所有出现的子胞腔，获得所有可能的解。对于某一个胞腔，指定了它的分解方法后，只要在枚举过程当中出现矛盾，那么这个枚举分支就被删除。

步骤五、对于二连通胞腔，它有两条边界，一条为内边界，另一条为外边界，每条边界都是由若干拓扑边组成的。为了求解二连通胞腔，有以下五个分析：

(1)若二连通胞腔的内外边界是不会被切割路径连接的，则可以分开求解。

如图5所示情形中，该方法希望通过中间的二连通胞腔(用同心圆表示)连接它邻接的第一胞腔和第二胞腔，使它们可以被末端执行器无抬起地执行。图5左侧部分是直接求解二连通胞腔，一共有五种可能的情况，图5右侧部分是先将内边界拿掉，然后对仅有外边界的胞腔(此时成为单连通胞腔)应用步骤四中所述的方法求解，最后再将内边界任意放置于求解后的胞腔中。容易看出图5的左右两侧是等价的。因此，对于二连通胞腔，若内边界是不被切割路径截断的，则可以先把内边界去掉，仅对外边界形成的单连通胞腔进行求解，而后再将内边界任意配置在胞腔中。

下面说明内外边界的地位是相同的。如图6所示，使用球极投影来展现内外边界的等价性。不妨将一个投影球放置在内边界中，则内边界在球面上的像为南极附近的一个圈，外边界在球面上的像也是一个圈，但是更靠近北极。将投影球的半径缩小至趋近于零，可以看到内、外边界的像分别成为了新的外、内边界，因此它们的角色可以互换。

综上，当二连通胞腔的切割路径不连接它的内、外边界时，二连通胞腔可以被分成两个单连通胞腔求解。

(2)如图7所示的循环切割路径是不需要被考虑的，因为它们等价于不循环的切割路径的解。如图8所示，将二连通胞腔的内边界连续地旋转，从而很容易看到循环切割路径和不循环切割路径的等价性。

(3)二连通胞腔的所有切割路径可以分为两种，一种是将二连通胞腔转化为单连通胞腔的切割路径，另一种可以看成是已经将二连通胞腔转化为单连通胞腔后，又在新生成的单连通胞腔中指定的切割路径。如图9中二连通胞腔的分解方法(图9左)可以看成是通过两步生成的：首先，通过上方和右侧的连接内、外边界的切割路径将二连通胞腔转化为单连通胞腔(图9中)，再在单连通胞腔中添加一条切割路径(图9右)。

(4)在(3)中所述的两种切割路径里，第一种切割路径的数量一定是两条，原因如下：首先，单条切割路径不能将二连通胞腔转化为单连通胞腔，而是只会导致矛盾，因为切割路径的存在意味着它的两侧胞腔最终会被指定为不同的编号，而连接二连通胞腔的内、外边界的切割路径的两侧是同一个胞腔，不可能指定为不同的编号；其次，若有两条以上连接内、外边界的切割路径(如图10左图所示)，则可以看成是先使用两条切割路径将二连通胞腔划分为两个单连通胞腔(图10中图)，再在某一个单连通胞腔内指定第三条切割路径(图10右图)。因此，二连通胞腔求解时一定是先切分为两个单连通胞腔，而后再进一步地分解。

(5)在二连通胞腔中设计两条连接内、外边界的切割路径，等价于在内、外边界上分别选出一列连续的拓扑边，并且指定它们为某一个生成出的单连通胞腔的边界。二连通胞腔的内、外边界上未被选中的拓扑边成为另一个生成出的单连通胞腔的拓扑边。假设二连通胞腔的内、外边界ω，ω′分别是由j，k个拓扑边按顺序排列的，拓扑边的编号分别为：

ω＝(α1，…，αj)

ω′＝(α′1，…，α′k)

其中，括号表示其中的元素排序是有顺序的。从这两个括号中分别选出一些连续排列的元素，并且为了避免循环选取，要求α1所在的子胞腔为第一个单连通胞腔。容易看出，在ω中一共有如下取法(在公式中，第i行中是选出i个元素的所有可能情况)：

同理，在ω′中一共有如下取法(在公式中，第i行中是选出i个元素的所有可能情况)：

因此，二连通胞腔的所有分解方法步骤如下：

(5.1)考虑不存在内外边界相连通的切割路径的情况，将内外边界分开，视作两个单连通胞腔各自求解；

(5.2)考虑内外边界相连通的切割路径，先设计两条连接内、外边界的切割路径，将二连通胞腔的分解问题转化为两个单连通胞腔的分解问题，而后使用步骤四中单连通胞腔的求解方法进行求解。

步骤六、对于n连通胞腔，n连通胞腔内部有n-1个内部边界，首先，由步骤五中的分析(1)可知，若这n-1个内边界中有任何一个是不被切割路径连接的，则可以先不考虑这个内边界，等到将剩下的部分分解完后，将这个边界放置到任意位置。又因为剩下的部分只有n-2个内边界，所以是一个n-1连通胞腔。由归纳假设，n-1连通胞腔的解法是已经给出的。因此，在有某一个内边界是不被任何切割路径连接的情况下的n连通胞腔可以如上求解。以下只需考虑“所有内边界都被切割路径连接”的情况。

因为在n连通胞腔中，只需要将任何一个内边界与外边界相连通，它就可以变成n-1连通胞腔，从而可以被求解，所以，考虑“将内边界一个一个放入外边界中”的策略，n连通胞腔的分解方法步骤如下：

(6.1)将n连通胞腔的n-1个内边界编号，其中外边界和第i个内边界包含的拓扑边分别用如下符号表示：

ω＝(α1，…，αk)

其中，αk表示该胞腔与它的第k个外部邻接胞腔之间的拓扑边，表示该胞腔与它的第i个内部边界上编号为j的胞腔之间的拓扑边。

(6.2)只考虑外边界ω和第一条内边界ω¹，根据步骤五中二连通胞腔的求解过程可知，由ω和ω¹构成的二连通胞腔中设计两条切割路径使之成为两个单连通胞腔。

(6.3)再将第二条内边界ω²放入(6.2)中生成的两个单连通子胞腔之一。

(6.4)对于(6.3)放置了ω²的那个单连通子胞腔成为了一个二连通子胞腔，将该二连通子胞腔重复步骤五，将其分为两个单连通子胞腔。此时，包含ω，ω¹，ω²的胞腔被分为了三个单连通子胞腔。

(6.5)对于后续的每个内边界ω³，…，ω^n-1，均依次执行(6.3)-(6.4)：将ω³，…，ω^n-1放入已经生成好的某个单连通子胞腔中使之变为二连通胞腔，并再切分为两个单连通子胞腔。在放入第i个内边界时，原胞腔已经被分为了i份。

(6.6)将n-1个内边界都放入胞腔中后，原胞腔被切分为n个单连通子胞腔，将这n个单连通子胞腔通过步骤四进行求解。

n连通胞腔的分解方法示意图如图11所示，遍历上述(1)～(5)中的所有不同情形，可以获得对单个胞腔的所有可能解，是因为有如下的等价关系：在将新的内边界插入至已有的边界以及已指定的切割路径中时，不需要考虑已有的切割路径穿过新的内边界的情形，而只需要将新的内边界放入已经生成好的子胞腔的内部，此等价关系的示意图如图12所示。

步骤七、根据步骤四-六的求解过程，使用迭代方式求解待覆盖物体表面上机械臂的运动学模型生成的拓扑图：

(7.1)对待覆盖物体表面上的第一胞腔，遍历所述第一胞腔的所有可能的切割方法并设置编号，即完成所述第一胞腔的所有解法。对所有解法中的每一个，执行步骤(7.2)；

(7.2)对待覆盖物体表面上的第二胞腔，遍历所述第二胞腔的所有可能的切割方法并设置编号，即完成所述第二胞腔的所有解法。将第二胞腔的所有解法与第一胞腔设定有矛盾的解删掉。对第二胞腔中剩下的可行解法中的每一个，执行步骤(7.3)；

(7.3)依次对待覆盖物体表面上的第三胞腔至第n胞腔执行步骤(7.2)，使得每个胞腔都被设置切割方法，且每个切出的子胞腔均为唯一的编号，即获得机械臂覆盖子胞腔的方式。

本方法的编号({c1，…，cn})指定策略是基于机械臂关节空间中的连续性构造出来的。当使用不同构型、不同维度的机械臂处理不同的物体表面时，连续性的定义可能会有变形。凡是根据机械臂关节空间的连续性对机械臂在覆盖任务中的可行位姿进行划分、目的是实现最少抬起次数的其它方法，均等价于指定了某种编号。所以这种变形应认为是本发明的保护范围。

本方法使用枚举遍历的方法获得非冗余机械臂接触覆盖任务中使得机械臂与物体表面解除接触次数最少的所有最优解。但是当仅对所有可能组合中的某一些进行检查时，也可以获得一些最优解，或者一些近似最优解。因此，不使用枚举策略，最终目的是为了获取此机械臂接触覆盖任务的一个最优解或者近似最优解的其它方法，也应认为是本发明的保护范围。

典型的机械臂的非冗余情形的工作场景举例如下：(1)使用五自由度机械臂覆盖三维物体表面区域，且末端执行器垂直于物体表面，如金属零件表面精加工，汽车表面抛光等(2)使用二自由度机械臂覆盖平面区域，如桌面擦拭等(3)使用四自由度机械臂完成三维物体表面区域喷漆(4)使用六自由度机械臂完成三维物体表面区域近距离观察。

实施例

非冗余机械臂需要覆盖形如“+”的区域，通过本发明方法步骤一求得机械臂覆盖物体表面每个点的逆运动学，得到的一组连续的位姿可以覆盖“-”，而另一组连续的位姿可以覆盖“|”。通过本发明方法步骤二的过程将所有位姿进行编号，将能够覆盖“-”的所有位姿编号为1，将能够覆盖“|”的所有位姿编号为2。通过步骤三进行胞腔的构建，构建出的拓扑图与图1相同，即可使用与图1中相同的胞腔编号。第一胞腔的可被覆盖的机械臂位姿为{1}，其中花括号表示其中元素的顺序没有特定含义；其邻接胞腔为(2)，其中小括号表示其中元素是按顺序排列的，可知第二、三、四、五胞腔的可被覆盖的机械臂位姿依次为{1，2}，{2}，{2}，{1}，其邻接胞腔依次为(1，4，5，3)，(2)，(2)，(2)。通过步骤四所述的求解方法，可知第一、三、四、五胞腔分别只有唯一一种选择编号的方法和切割方法，因此只需要对第二胞腔进行求解。经过求解，可知第二胞腔的(1)切割方式为1010且编号设置为1，或者(2)切割方式为0101且编号设置为2时，该问题可以取得最优解。这两个解的物理含义分别为(1)先使用编号为1的位姿覆盖第一、二、五胞腔所在区域，而后抬起一次，使用编号为2的位姿覆盖第三胞腔所在区域，而后再抬起一次，最终使用编号为2的位姿覆盖第四胞腔所在区域。(2)先使用编号为2的位姿覆盖第二、三、四胞腔所在区域，而后抬起一次，使用编号为1的位姿覆盖第一胞腔所在区域，而后再抬起一次，最终使用编号为1的位姿覆盖第五胞腔所在区域。通过上述两种方法求得最少抬起次数均为2。

最后，还需要注意的是本发明不限于以上实施例，还可以有许多变形。本领域的普通技术人员能从本发明公开的内容直接导出或联想到的所有变形，均应认为是本发明的保护范围。