一种基于人工SPP波导的可调二次谐波激发结构及方法与流程

本发明涉及一种基于人工spp波导的可调二次谐波激发结构及方法，属于通信和新型人工电磁材料领域。

背景技术：

表面等离极化激元(spps)是由外界电磁场与金属电子在光学频率下的振荡耦合而产生的。它是沿金属和电介质界面传播的表面电磁波，具有慢波特性，进而导致了较强的场束缚能力。然而，spps不能传播在微波频段，由于金属的电导体特性。在2004年j.b.pandry教授证明了一种二维通孔阵列形式的结构，可使电磁波束缚在结构表面，构成类似spps的表面波即人工spps。为了便于使其应用到集成电路，东南大学的崔铁军课题组在2013年提出了一种具有共性特性的表面等离激元结构。近年来，基于人工spps的传输线结构被研究，并且和传统的微带线相比，它具有低弯折损耗、抗干扰、低串扰和小型化等优势。

由于spps的场增强作用，基于人工spp结构的非线性效应得到了广泛的关注。在2011年，d.r.smith教授提出了在开口谐振环的缝隙处加载非线性器件，进而提高二次谐波的产生，但是上述的非线性波导不易于集成。此后，场效应管和变容二极管被引入到一维的人工spp波导上，进而激发正向的二次谐波，然而这些情况下激发的二次谐波的传输是单方向的，此限制了一些潜在的应用。

技术实现要素：

技术问题：为实现动态可调的二次谐波产生，本发明提供一种在正向/反向相位匹配的条件下，通过在人工spp波导中加载有源器件的实现最大转化效率的正向/反向二次谐波的技术方法。

技术方案：本发明的传输线平面以介质基板为载体，由人工spp波导和变容二极管构成。特殊开口谐振环结构单元中加载的变容二极管是不同的，结构上方的两个变容二极管(c1)是线性的，而结构下方的变容二极管(c2)是非线性的。在开口谐振环结构参数不变的情况下，人工spp结构单元的色散特性由变容二极管的电容值决定，因此，正向和反向相位匹配可实现，最大转化效率的二次谐波产生。

有益效果：与现有技术相比，本发明的优势：

1.本发明仅通过在人工spp波导加载有源器件即可实现非线性二次谐波的产生，操作简单，节省空间，便于小型化。

2.本发明通过调节有源器件的电容值进而改变人工spp波导的色散特性，实现在同一频段内的正向和反向相位匹配，进而激发最大效率的正向和反向二次谐波。

3.本发明解决了在同一人工spp波导情况下，通过调节变容二极管上的偏压可实现正向和反向二次谐波的产生，可较好地应用于集成电路，通信系统和非线性spp系统。

附图说明

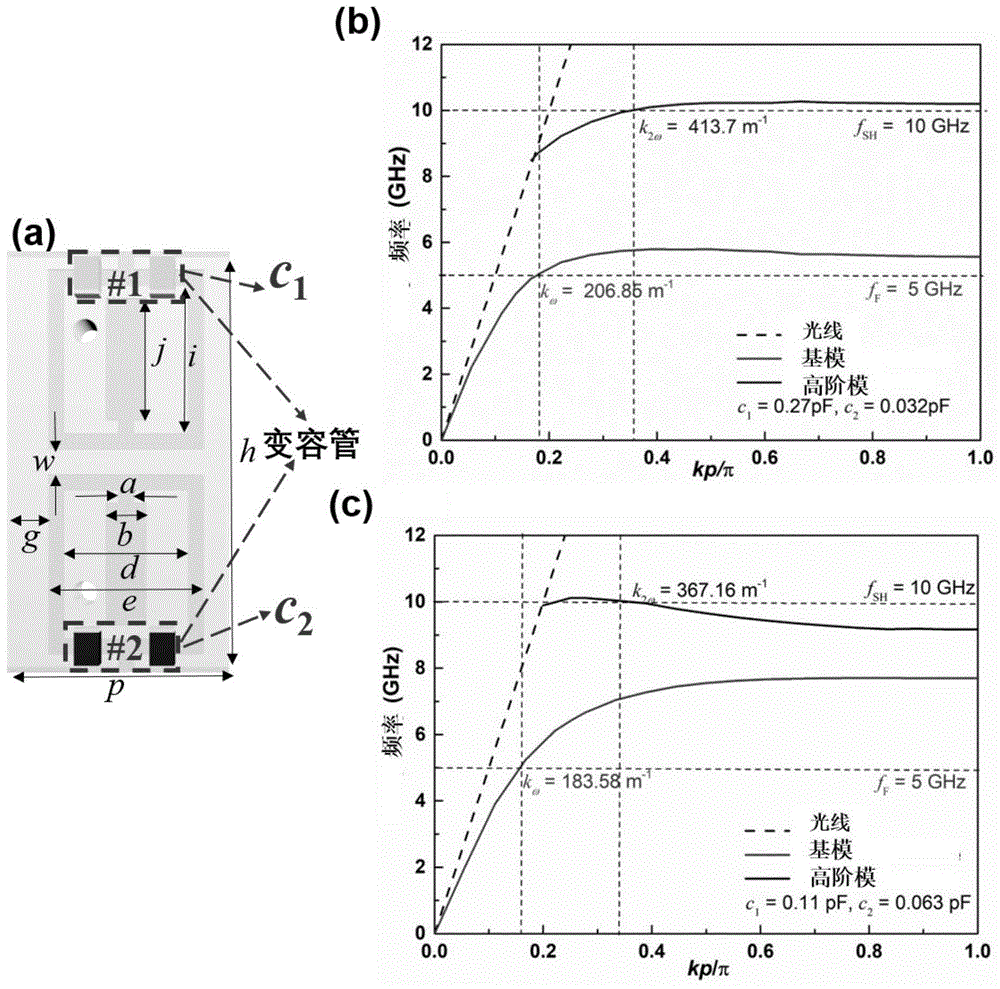
图1是非线性人工spp波导的单元结构示意图及其色散曲线，其中，图1(a)是加载变容管的几何单元结构，图1(b)和图1(c)是不同电容值对应的色散曲线；

图2是非线性人工spp波导中二次谐波激发的正向和反向相位匹配条件，其中，图2(a)是正向相位匹配条件下二次谐波产生(k2ω＝2kω,n2ω＝nω)，图2(b)是反向相位匹配条件下二次谐波产生(k2ω＝-2kω,n2ω＝nω)，其中nω，n2ω分别为基模和高阶模的折射率；

图3是在不同偏压下正向和反向相位匹配的二次谐波产生，其中，图3(a)是正向二次谐波的转化效率，图3(b)是反向二次谐波的转化效率。

具体实施方式

下面结合附图和具体实施例对本发明的技术方案进行详细的说明。

本发明利用人工spps的场增强作用，并把引入的变容二极管作为非线性器件,进而通过调节加载在变容二极管的偏压，实现在正向/反向相位匹配条件下最大效率的正向/反向二次谐波产生。

非线性人工spp波导的单元结构如图1(a)所示。其中单元周期p＝2mm，宽度h＝5mm，a＝0.2mm,b＝0.5mm,d＝1.5mm,e＝1.9mm,g＝0.5mm,p＝2.7mm,w＝0.3mm,i＝1.8mm,j＝1.5mm，介质基板f4b的介电常数为2.65，厚度为0.813mm，损耗正切角为0.001。用商业软件cst进行本征模仿真可得其色散曲线如图1(b)和图1(c)所示，通过改变变容二极管的电容值，可以实现在相同的频率下改变高阶模下群速度的方向(群速度的方向与电磁能量传播的方向一致)。当c1＝0.27pf和c2＝0.032pf时，正向的相位匹配条件为kω＝206.85m^-1(ff＝5ghz)andk2ω＝413.7m^-1(fsh＝10ghz)。改变变容管的电容值，当c1＝0.11pf和c2＝0.063pf时，反向的相位匹配条件为kω＝183.58m^-1(ff＝5ghz)andk2ω＝367.16m^-1(fsh＝10ghz)。另外，正向和反向的相位匹配可在一点频段范围内实现。

如图3(a)和3(b)所示，在相位匹配频点，二次谐波产生的效率最高。转化效率可由得到

式中，i2ω和iω为二次谐波和基波的能量密度，l为非线性区域的长度，deff为有效的非线性极化率，nω和λω为基波下的折射率和波长，υ和ε0为自由空间中的传播速度和介电常数，δk为相位失配。从式中可以看出，当其他参数为定值时，二次谐波的转化效率仅与δk有关，因此二次谐波的转化效率如图3。