编码器、解码器以及用于编码和解码的方法与流程

本发明的实施例涉及用于对音频信号进行编码以获得数据流的编码器以及用于对数据流进行解码以获得音频信号的解码器。其他实施例涉及用于对音频信号进行编码以及用于对数据流进行解码的对应方法。又一实施例涉及进行用于编码和/或解码的方法的步骤的计算机程序。

背景技术：

待被编码的音频信号可以，例如，为语音信号；即编码器与语音编码器相对应且解码器与语音解码器相对应。语音编码中最常用的范例为用于诸如AMR-家族、G.718以及MPEG USAC的标准中的代数码激励线性预测(ACELP)。它基于使用源模型的建模语音，由用于对频谱包络进行建模的线性预测器(LP)、用于对基频进行建模的长期预测器(LTP)以及用于残差的代数码本组成。在感知加权合成域中，码本参数被优化。感知模型基于滤波器，由此，通过线性预测器和加权滤波器的组合描述从残差至加权输出的映射。

ACELP编解码器中的计算复杂度的最大部分花费在选择代数码本条目上，其基于残差的量化。从残差域至加权合成域的映射本质上是乘以大小为N×N的矩阵，其中N为向量长度。由于此映射，就加权输出SNR(信噪比)而言，残差样本是相关的且无法被独立地量化。由此得出结论，在加权合成域中，需要明确地评估每个可能的码本向量以确定最佳条目。此方法被称为合成-分析算法。仅利用码本的暴力搜索，最优性能是可能的。码本大小取决于比特率，但考虑B的比特率，存在2^B个条目需要评估，总复杂度为O(2^BN²)，当B大于或等于11时，这明显是不切实际的。在实际中，编解码器因此利用在复杂度和质量之间权衡的非最优量化。已存在一些用于找到以准确率为代价限制复杂度的最佳量化的迭代算法。为了克服此限制，需要新方法。

技术实现要素：

本发明的目的在于提供一种用于编码和解码音频信号同时避免上述缺陷的概念。

通过独立权利要求实现此目的。

第一实施例提供一种用于将音频信号编码为数据流的编码器。该编码器包括：(线性或长期)预测器、因子分解器(factorizer)、变换器、以及量化的编码阶段。预测器用于分析音频信号以获得描述音频信号的频谱包络或音频信号的基频的(线性或长期)预测系数并用于使得音频信号服从取决于预测系数的分析滤波函数以输出音频信号的残差信号。因子分解器用于将矩阵因子分解应用于由预测系数定义的合成滤波函数的自相关或协方差矩阵以获得经因子分解的矩阵。变换器用于基于经因子分解的矩阵对残差信号进行变换以获得变换的残差信号。量化和编码阶段用于对变换的残差信号进行量化以获得量化后的变换的残差信号或经编码的量化后的变换的残差信号。

另一实施例提供一种用于将数据流解码为音频信号的解码器。该解码器包括：解码阶段、再变换器以及合成阶段。解码阶段用于基于入站的量化后的变换的残差信号或基于入站的经编码的量化后的变换的残差信号输出变换的残差信号。再变换器用于基于从合成滤波函数的自相关或协方差矩阵的矩阵因子分解产生的经因子分解的矩阵，从变换的残差信号再变换为残差信号，合成滤波函数由描述音频信号的频谱包络或音频信号的基频的预测系数定义。合成阶段用于通过使用由预测系数定义的合成滤波函数基于残差信号合成音频信号。

正如基于这两个实施例可见的，编码和解码为使得此概念可比拟于ACELP的两阶段过程。第一步骤使能关于频谱包络或基频的合成的量化，其中第二阶段能够实现残差信号(也称为激励信号并表示在利用音频信号的频谱包络或基频对信号进行滤波之后的信号)的(直接)量化或合成。同样，类似于ACELP，残差信号或激励信号的量化遵守优化问题，其中与ACELP相比，根据本文中所公开的教示的优化问题的目标函数存在本质区别。详细地，本发明的教示基于矩阵因子分解用于对优化问题的目标函数进行去相关，由此可避免计算昂贵的迭代并保证最优性能的原理。作为所附实施例的一个核心步骤的矩阵因子分解包括于编码器实施例中，且优选地而非必须地可包括于解码器实施例中。

矩阵分子分解可基于不同技术，例如特征值分解、范德蒙因子分解或任何其他因子分解，其中，对于每种所选的技术，因子分解进行因子分解的是矩阵，如由编码或解码的第一阶段(线性预测器或长期预测器)中的第一音频检测到的(线性或长期)预测系数定义的合成滤波函数的自相关或协方差矩阵。

根据另一实施例，因子分解器对包括使用矩阵存储的预测系数的合成滤波函数进行因子分解，并对合成滤波函数矩阵的加权形式进行因子分解。例如，可通过使用范德蒙矩阵V、对角矩阵D以及范德蒙矩阵的共轭变换形式V^＊进行因子分解。可使用公式R＝V^*DV或C＝V^＊DV对范德蒙矩阵进行因子分解，其中自相关矩阵R或协方差矩阵C由合成滤波函数矩阵的共轭变换形式H^＊以及合成函数矩阵H的正则形式定义，即R＝H^＊H或C＝H^*H。

根据又一实施例，变换器，从先前确定的对角矩阵D的和先前确定的范德蒙矩阵V，使用公式y＝D^1/2Vx或公式y＝DVx将残差信号x变换为变换的残差信号y。

根据又一实施例，量化和编码阶段此刻能够对变换的残差信号y进行量化以获得量化后的变换的残差信号此变换为优化问题，如上所论述，其中使用目标函数此处，有利的是，与用于不同的编码或解码方法的目标函数(如，ACELP编码器中使用的目标函数)相比，此目标函数具有减小的复杂度。

根据实施例，解码器从编码器接收经因子分解的矩阵，如和数据流一起。或根据另一实施例，解码器包括进行矩阵因子分解的可选的因子分解器。根据优选实施例，解码器直接接收经因子分解的矩阵并从这些经因子分解的矩阵得到预测系数，因为矩阵都源于预测系数(参看编码器)。此实施例能够实现进一步地减小解码器的复杂度。

又一实施例提供用于将音频信号编码为数据流以及用于将数据流解码为音频信号的对应方法。根据附加实施例，用于编码的方法以及用于解码的方法可由或至少部分地可由诸如计算机的CPU的处理器进行。

附图说明

将参考所附附图论述本发明的实施例，其中

图1a显示根据第一实施例的用于对音频信号进行编码的编码器的示意性框图；

图1b显示根据第一实施例的用于对音频信号进行编码的对应方法的示意性流程图；

图2a显示根据第二实施例的用于对数据流进行解码的解码器的示意性框图；

图2b显示根据第二实施例的用于对数据流进行解码的对应方法的示意性流程图；

图3a显示示出对于不同量化方法的作为每帧比特数的函数的平均感知信噪比的示意图；

图3b显示示出作为每帧比特数的函数的不同量化方法的归一化运行时间的示意图；以及

图3c显示示出范德蒙变换的特征的示意图。

具体实施方式

随后以下将参考所附附图详细地论述本发明的实施例。此处，为具有相同或相似功能的对象提供相同的附图标记，以使得其描述为可互换或互相适用的。

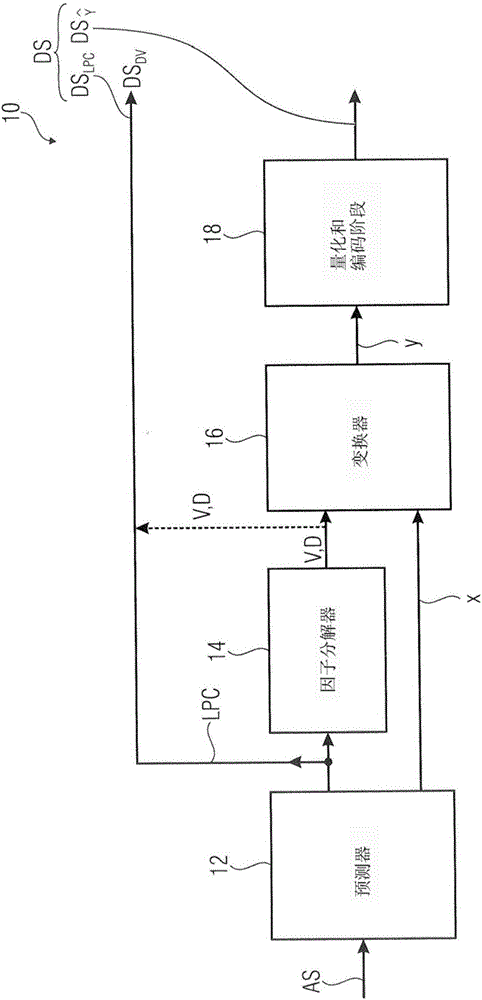
图1显示基本配置中的编码器10。编码器10包括：此处被实施为线性预测器12的预测器12、以及因子分解器14、变换器16以及量化和编码阶段18。

线性预测器12布置于输入处以接收音频信号AS，优选地，数字音频信号，如脉冲码调制信号(PCM)。线性预测器12经由所谓的LPC信道LPC连接至因子分解器14和编码器的输出处，参看附图标记DS_LPC/DS_DV。更进一步地，线性预测器12经由所谓的残差信道连接至变换器16。反之亦然，变换器16在其输入侧(除残差信道之外)连接至因子分解器14。在其输出侧，变换器连接至量化和编码阶段18，其中量化和编码阶段18连接至输出(参看附图标记)。两个数据流DS_LPC/DS_DV和形成待被输出的数据流DS。

以下将论述编码器10的功能，其中额外参考描述用于编码的方法100的图1b。如根据图1b可见的，用于将音频信号AS编码为数据流DS的基本方法100包括由单元12、14、16和18进行的四个基本步骤120、140、160和180。在第一步骤120中，线性预测器12分析音频信号AS以获得线性预测系数LPC。之后，描述音频信号AS的频谱包络的线性预测系数LPC使得能够使用所谓的合成滤波函数H去基本地合成音频信号。合成滤波函数H可包括由LPC系数定义的合成滤波函数的加权值。使用LPC信道LPC，线性预测系数LPC被输出至因子分解器14，以及被转发至编码器10的输出处。线性预测器12更进一步地使得音频信号AS服从由线性预测系数LPC定义的分析滤波函数H。此过程为由解码器进行的基于LPC系数的音频信号的合成的对应部分。此子步骤的结果是被输出至变换器16的残差信号x，而没有由滤波函数H可描述的信号部分。请注意，此步骤是逐帧进行的，即，具有振幅和时域的音频信号AS被划分或采样至如具有5毫秒的长度的时窗(样本)，并在频域中被量化。

随后的步骤为由变换器16进行的残差信号x的变换(参看方法步骤160)。变换器16用于对残差信号x进行变换以获得被输出至量化和编码阶段18的变换的残差信号y。例如，变换160可基于公式y＝D^1/2Vx或公式y＝DVx，其中矩阵D和V由因子分解器14提供。因此，残差信号x的变换基于至少两个经因子分解的矩阵V(示例性地被称为范德蒙矩阵)和D(示例性地被称为对角矩阵)。

所应用的矩阵因子分解可被自由地选作，例如，特征值分解、范德蒙因子分解、乔里斯基(Cholesky)分解或类似。范德蒙因子分解可用作对称、正定的托普利兹(Toeplitz)矩阵(如自相关矩阵)至范德蒙矩阵V和V^＊的乘积的因子分解。对于目标函数中的自相关矩阵，此与通常称作范德蒙变换的翘曲离散傅立叶变换相对应。在论述量化和编码阶段18的功能之后，将详细论述由因子分解器14进行的表示本发明的基础部分的矩阵因子分解的此步骤140。

量化和编码阶段18对从变换器16接收的变换的残差信号y进行量化，以获得量化后的变换的残差信号此变换的量化后的残差信号作为数据流的部分被输出。请注意，整个数据流DS包括由DS_LPC/DS_DV指示的LPC-部分以及由指示的部分。

例如，使用目标函数，例如，依据可进行变换的残差信号y的量化。与ACELP编码器的典型目标函数相比，此目标函数具有减小的复杂度，以使得编码关于其性能被有利地改进。此性能改进可用于对具有较高分辨率的音频信号AS进行编码或用于减少所需资源。

应注意的是，信号可为经编码的信号，其中编码由量化和编码阶段18进行。因此，根据其他实施例，量化和编码阶段18可包括可用于算术编码的编码器。量化和编码阶段18的编码器可使用线性量化步骤(即，等距离)或诸如对数的、可变的量化步骤。可选地，编码器可用于进行其他(无损)熵编码，其中码长度随着奇异(singular)输入信号AS的概率的函数而改变。因此，为了获得优选码长度，作为可选选项，可以基于合成包络以及因此基于LPC系数检测输入信号的概率。因此，量化的编码阶段还可具有用于LPC信道的输入。

以下，将论述能够实现目标函数η(y)的复杂度减小的背景。如以上所提及的，改进的编码基于由因子分解器14进行的矩阵因子分解的步骤140。因子分解器14对诸如由线性预测系数LPC(参看LPC信道)定义的滤波合成函数H的自相关矩阵R或协方差矩阵C的矩阵进行因子分解。此因子分解的结果为两个经因子分解的矩阵，例如，表示包括奇异LPC系数的原始矩阵H的范德蒙矩阵V和对角矩阵D。由于此，残差信号x的样本为去相关的。由此得出结论，变换的残差信号的直接量化(参看步骤180)为最优量化，由此计算复杂度几乎独立于比特率。相比之下，用于ACELP码本的优化的传统方法必须在计算复杂度和准确率之间进行权衡，尤其是在高比特率处。因此，实际上从传统ACELP进程开始论述背景。

ACELP的传统目标函数采用协方差矩阵的形式。根据改进的方法，存在应用加权合成函数的自相关矩阵的可选目标函数。基于ACELP的编解码器优化感知加权合成域中的信噪比(SNR)。目标函数可被表示为：

其中，x是目标残差，为量化后的残差，H为与加权合成滤波相对应的卷积矩阵，以及γ为比例增益系数。为了找到最优量化标准方法为在η(x，γ)的导数为0处找到由γ^＊指示的γ的最优值。通过将最优γ^＊插入等式(1)，获得新的目标函数：

其中，H^*是合成函数H的共轭变换形式。

请注意，传统方法H是下三角方卷积矩阵，由此，协方差矩阵C＝H^＊H为对称的协方差矩阵。以全尺寸卷积矩阵对下三角矩阵的替代(由此，自相关矩阵R＝H^＊H为对称的自相关矩阵)与加权合成滤波的其他相关相对应。此替代给出显著减小的复杂度，而对质量的影响最小。

线性预测器14可使用协方差矩阵C或自相关矩阵R用于矩阵因子分解。以下论述针对这样的假设作出：自相关R用于通过取决于LPC系数的矩阵的因子分解修改目标函数。通过包括特征值分解的一些方法，诸如R的对称正定定义的托普利兹矩阵可被分解为：

R＝V^＊DV (3)

此处，V^*为范德蒙矩阵V的共轭变换形式。在使用协方差矩阵C的传统方法中，可应用其他因子分解，如奇异值分解C＝USV。

对于自相关矩阵，还可使用以等式(3)的形式的可选因子分解，此处可被称为范德蒙因子分解。范德蒙因子分解为能够实现因子分解/变换的新概念。范德蒙矩阵具有|v_k|＝1的值以及

的V。并且，D为具有严格正条目的对角矩阵。可以以复杂度为O(N³)的任意精度计算分解。直接分解具有为O(N^3)的典型计算复杂度，但在此处计算复杂度可被降低至O(N^2)，或如果近似因子分解是足够的，则复杂度可降低至O(N log N)。对于所选中的分解，可被定义为：

其中，x＝V^-1D^-1/2_y，且将其插入等式(2)可得到：

请注意，此处，y的样本并非是彼此相关的，且以上的目标函数不过是目标与量化后的残差之间的归一化相关。由此可得出结论，y的样本可被独立地量化，且如果所有样本的准确率是相等的，则此量化引致最佳的可能准确率。

在范德蒙因子分解的情况下，由于V具有|v_k|＝1的值，它与翘曲离散傅立叶变换相对应，且y的元素与残差的频率分量相对应。更进一步地，乘以对角矩阵D与频带的比例缩放相对应，且由此可得出结论，y为残差的频域表示。

与此相反，当特征值分解与傅立叶变换一致时，特征值分解仅在窗口长度接近无穷时具有物理解释。有限长度的特征值分解因此松散地与信号的频率表示相关，但将分量标记至频率是困难的。再者，已知特征值分解是优化基础，由此它可在某些情况下给出最佳性能。

始于这两个经因子分解的V和D，变换器16进行变换160，以便使用由等式(5)定义的去相关的向量而对残差信号x进行变换。

假定x是非相关的白噪声，则Vx的样本也将具有相等的能量期望。据此，可使用算术编码器或使用代数码本来对值进行编码的编码器。然而，Vx的量化并非是关于目标函数最优的，因为它忽略了对角矩阵D^1/2。另一方面，全变换y＝D^1/2Vx包括通过对角矩阵D的比例缩放，这改变了y的样本的能量期望。创建具有非均匀方差的代数码本并非是无关紧要的。因此，可将使用算术码本而非获得最优比特消耗作为一种选项。然后可定义算术编码，正如[14]中所披露的。

请注意，如果使用分解，如范德蒙变换或其他复杂变换，则实部和虚部为独立的随机变量。如果复变量的方差为σ²，则实部和虚部具有σ²/2的方差。诸如特征值分解的实值分解仅提供实值，由此实部和虚部的分离并非必须的。为了利用复值变换的更高性能，可应用用于复值的算术编码的传统方法。

根据以上实施例，预测系数LPC(参看DS_LPC)被输出为LSF信号(线谱频率信号)，其中，输出经因子分解的矩阵V和D(参看DS_DV)内的预测系数LPC是可选选项。此可选选项通过由V、D标记的虚线以及DS_DV是由因子分解器14的输出产生的指示暗示。

因此，本发明的另一实施例涉及包括两个经因子分解的矩阵(DS_VD)的形式的预测系数LPC的数据流(DS)。

关于图2，将论述解码器20和用于解码的对应方法200。

图2a显示包括解码阶段22、可选的因子分解器24、再变换器26以及合成阶段28的解码器20。解码阶段22以及因子分解器24被布置于解码器20的输入处，且因此用于接收数据流DS。详细地，数据流DS的第一部分，即线性预测系数，被提供至可选的因子分解器24(参看DS_LPC/DS_DV)，其中第二部分，即量化后的变换的残差信号或经编码的量化后的变换的残差信号被提供至解码阶段22(参看)。合成阶段28被布置于解码器20的输出处，并用于输出类似但不等于音频信号AS的音频信号AS’。

音频信号AS’的合成基于LPC系数(参看DS_LPC/DS_DV)且基于残差信号x。因此，合成阶段28连接至输入以接收DS_LPC信号以及连接至提供残差信号x的再变换器26。再变换器26基于变换的残差信号y且基于至少两个经因子分解的矩阵V和D计算残差信号x。因此，再变换器26具有至少两个输入，即用于(例如)从因子分解器24接收V和D的第一输入，以及用于从解码器阶段接收变换的残差信号y的一个输入。

以下将参考图2b示出的对应方法200详细地论述解码器20的功能。解码器20(从编码器)接收数据流DS。此数据信号DS使得解码器20能够合成音频信号AS’，其中由DS_LPC/DS_DV指示的数据流的部分能够实现基本信号的合成，其中由指示的部分能够实现音频信号AS’的细节部分的合成。在第一步骤220中，解码器阶段22对入站的信号进行解码，并将变换的残差信号y输出至再变换器26(参看步骤260)。

并行的或串行的，因子分解器24进行因子分解(参看步骤240)。如关于步骤140所论述的，因子分解器24将矩阵因子分解应用于合成滤波函数H的自相关矩阵R或协方差矩阵C，即，解码器20所使用的因子分解类似或接近类似于在编码的上下文中描述的因子分解(参看方法100)，且因此可为如上所论述的特征值分解或Cholesky因子分解。此处，合成滤波函数H得自入站的数据流DS_LPC/DS_DV。更进一步地，因子分解器24将两个经因子分解的矩阵V和D输出至再变换器26。

基于两个矩阵V和D，再变换器26从变换的残差信号y再变换为残差信号x并将x输出至合成阶段28(参看步骤280)。合成阶段28基于残差信号x以及基于作为数据流DS_LPC/DS_DV接收的LPC系数LPC合成音频信号AS’。应注意的是，音频信号AS’类似但不等于音频信号AS，因为由编码器10进行的量化并非是无损的。

根据另一实施例，经因子分解的矩阵V和D可被从另一实体(例如，直接从编码器10)提供至再变换器26(作为数据流的部分)。因此，解码器20的因子分解器24以及矩阵因子分解的步骤240为可选的实体/步骤，且因此由虚线示出。此处，作为可选的选项，预测系数LPC(合成280基于此进行)可得自入站的经因子分解的矩阵V和D。换句话说，这意味着数据流DS包括和矩阵V和D(即DS_DV)而非和DS_LPC。

以下关于图3a和3b论述以上所述的编码(以及解码)的性能改进。

图3a显示示出作为用于对可接收长度并等于64帧进行编码的比特的函数的平均感知信噪比的示意图。在图中，示出用于五个不同量化方法的5条曲线，其中两个方法即最优量化和逐对迭代量化为传统方法。公式(1)形成此对比的基础。作为所提议的去相关方法的量化性能与残差信号的传统时域表示的对比，ACELP编解码器已被实施如下。输入信号被再采样至12.8kHz，且利用在每一帧中心的长为32毫秒的汉明(Hamming)窗口估计线性预测器。然后，对于长为5毫秒并与AMR-WB编解码器的子帧相对应的帧，计算预测残差。利用穷举搜索，以32至150个样本之间的整数滞后对长期预测器进行优化。最优值用于未量化的LTP增益。

以(1-0.68z^-1)滤波的预加重被应用于输入信号，且像在AMR-WB中一样应用于合成中。所应用的感知加权为A(0.92z^-1)，其中A(z)为线性预测滤波。

为了评估性能，需要对比所提议的量化与传统方法(最优量化和逐对迭代量化)。最常用的方法将长为64帧的帧的残差信号划分至4个交错的通道。利用两种方式即以穷举搜索尝试所有组合的最优量化(参看Opt)方法或通过在每个可能位置尝试两个脉冲以连续地添加两个脉冲的逐对迭代量化(参看，Pair)，应用此方法。

前者对于每帧大于15个比特数的比特率变得计算上不可行且复杂的，而后者为次优的。请注意，后者也比应用于诸如AMR-WB的编解码器中的现有技术水平的方式更复杂，但因此也更有可能引致较佳的信噪比。将传统方式与以上论述的用于量化的算法进行对比。

范德蒙量化(参看Vand)通过y＝D^1/2Vx对残差向量x进行变换，其中从范德蒙因子分解获得矩阵V和D并使用算术编码器进行量化。特征值量化(参看Eig)类似于范德蒙量化，但矩阵V和D是通过特征值分解获得的。更进一步地，还可应用FFT量化(参看FFT)，即根据另一实施例，在y＝D^1/2Vx的变换处使用滤波的加窗的组合可被用于代替信号处理算法中的离散傅立叶变换(DFT)、离散余弦变换(DCT)、修正型离散余弦变换(MDCT)或其他变换。采取残差信号的FFT(快速傅立叶变换)，其中应用关于范德蒙量化的相同算术编码器。FFT方法将明显地给出低下质量，因为众所周知将等式(2)中的样本之间的相关考虑在内是很重要的。此量化因此为较低的参照点。

所述方法的性能的展示由评估如等式(1)所定义的平均长感知信噪比和方法复杂度的图3a示出。可清楚地看出，如所预期的，FFT域中的量化给出最差的信噪比。低下的性能可归因于此量化未将残差样本之间的相关考虑在内的事实。更进一步地，可声明的是，时域残差信号的最优量化等于以每帧5个和10个比特的逐对优化，因为在这些比特率下，存在仅1或2个脉冲，由此这些方法恰好是相同的。正如所预期的，对于每帧15个比特，最优方法稍微优于逐对优化。

在每帧10个比特或以上处，范德蒙域中的量化优于时域量化且特征值域为优于范德蒙域的一个步骤。在每帧5个比特处，算术编码器的性能更有可能迅速地降低，因为已知对于非常稀疏的信号它是次优的。

还观察到，在每帧80个比特以上，逐对方法开始偏离逐对方法。非正式实验显示，此趋势在更高比特率处增大，以使得最终FFT和逐对方法达到远低于特征值和范德蒙方法的类似信噪比。与此相反，特征值和范德蒙值继续为比特率的大约线性函数。特征值方法始终近似优于范德蒙方法0.36dB。假设此差值的至少部分由算术编码器中实部和复部的隔离解释。为了最优性能，实部和复部应被联合地编码。

图3b显示用于示出不同算法的复杂度的估计的以每比特率的每个方法的运行时间的测量。可看出，在低比特率处，最优时域方法的复杂度(参看Opt)已激增。时域残差的逐对优化(参看Pair)反而作为比特率的函数线性地增大。请注意，现有技术水平的方法限制逐对方法的复杂度，以使得该复杂度对于高比特率变成常数，虽然在此种限制下仍无法达到图3a示出的实验的有竞争性的信噪比结果。进一步地，两种去相关方法(参看Eig和Vand)以及FFT方法(参看FFT)对全体比特率近似地为恒定的。范德蒙变换在以上实施中具有比特征值分解方法高大体50％的复杂度，但对于此的原因可由MATLAB提供的特征值分解的高度优化版本的使用来解释，然而，范德蒙因子分解并非最优实施。然而，重要地，在每帧100个比特的比特率处，逐对优化的ACELP的复杂度分别相当于基于范德蒙算法的大体30倍和50倍。仅FFT快于特征值分解方法，然而由于FFT的信噪比是低下的，它并非可行的选项。

总之，以上所述的方法具有两个显著的益处。首先，通过在感知域中应用量化，感知信噪比被改进。其次，由于残差信号为去相关的(关于目标函数)，可直接地应用量化而无需高度复杂的合成分析环。由此得出结论，所提议的方法的计算复杂度关于比特率是几乎不变的，然而传统方法随着增大比特率而变得愈加复杂。

以上提出的方法完全不可利用传统语音和音频编码方法操作。具体地，目标函数的去相关可被应用于诸如MPEG USAC或AMR-WB+的编解码器的ACELP模式，而不限于编解码器中存在的其他手段。其中应用核心带宽或带宽扩展方法的方式将保持相同，且无需改变ACELP中的长期预测、共振峰增强、低音后置滤波等的方式以及实施此种不同编码模式(如ACELP和TCX)以及在这些模式之间切换的方式将不会受到目标函数的去相关的影响。

另一方面，明显的是，可轻松地重新用公式表示使用相同目标函数(参看公式(1))的所有手段(即，至少所有的ACELP实施)以利用去相关。因此，根据又一实施例，例如，可应用对长期预测贡献的去相关，且因此可使用去相关的信号计算增益因子。

此外，由于所提出的变换域为频域表示，根据其他实施例，可将频域语音和音频编解码器的典型方法应用至此新域。根据特定实施例，在频谱线的量化中，可应用死区以增大效率。根据另一实施例，可应用噪声填充以避免频谱缺陷。

尽管已经使用线性预测器在编码器的上下文中论述编码的以上实施例(参看图1a和图1b)，应当注意的是，预测器还可用于包含长期预测器以确定描述音频信号AS的基频的长期预测系数并基于由长期预测系数定义的滤波函数对音频信号AS进行滤波，以及输出残差信号x用于进一步处理。根据又一实施例，预测器可为线性预测器和长期预测器的组合。

清楚的是，可轻松地将所提议的变换应用至语音和音频处理中的其他任务，如语音增强。首先，基于子空间的方法基于信号的特征值分解或奇异值分解。由于所提出的方法基于类似分解，基于子空间分析的语音增强方法可适于根据又一实施例所提议的域。与传统子空间方法的不同在于，基于线性预测和残差域中的加窗的信号模型在何时被应用，如被应用于ACELP中。与此相反，传统子空间方法应用随时间固定(非适应性)的重叠窗口。

其次，基于范德蒙去相关的去相关提供类似于由离散傅立叶、余弦或其他类似变换所提供的频域。因此也可将常常在傅立叶、余弦或类似变换域中进行的任何语音处理算法以最小的修改应用于以上所述方法的变换域中。因此，可应用在变换域中使用频谱减法的语音增强，即这意味着，根据其他实施例，所提议的变换可用于语音或音频增强，例如，利用频谱减法、子空间分析的方法或它们的衍生或变型。此处，益处在于，此方法使用与ACELP相同的加窗，以便语音增强算法可紧紧地集成于语音编解码器中。更进一步地，ACELP的窗口具有比用于传统子空间分析中的那些窗口低的算法延迟。因而，加窗因此基于更高性能的信号模型。

参考用于变换器14中(即步骤140内)的等式(5)，应注意的是，它们的产物也可是不同的，例如，以y＝DVx的形状。

根据又一实施例，编码器10可包括位于输出处的用于将两个数据流DS_LPC/DS_DV和封包至共同封包DS的封包器。反之亦然，解码器20可包括用于将数据流DS分成两个包DS_LPC/DS_DV和的解封包器。

尽管已在装置的上下文中描述一些方面，显然的是，这些方面也表示对应方法的描述，其中区块或装置对应于方法步骤或方法步骤的特征。类似地，在方法步骤的上下文中所描述的方面也表示对应装置的对应区块或项目或特征的描述。方法步骤中的一些或所有可由(或使用)像诸如微处理器、可编程计算机或电子电路的硬件装置执行。在一些实施例中，最重要方法步骤的某个或某些可由此装置执行。

本发明的经编码的信号可储存在数字存储介质上或可在传输介质上(例如无线传输介质或有线传输介质(例如因特网))上传输。

取决于特定的实施要求，本发明的实施例可以以硬件或软件实施。可使用具有存储于其上的电子可读控制信号的数字存储介质，例如软性磁盘、DVD、蓝光、CD、ROM、PROM、EPROM、EEPROM或闪存，执行实施方案，这些电子可读控制信号与可编程计算机系统协作(或能够协作)以使得执行各个方法。因此，数字存储介质可为计算机可读的。

根据本发明的一些实施例包括具有电子可读控制信号的数据载体，这些电子可读控制信号能够与可编程计算机系统协作，使得执行本文中所描述的方法中的一个。

通常，本发明的实施例可被实施为具有程序代码的计算机程序产品，当计算机程序产品运行于计算机上时，程序代码操作性地用于执行这些方法中的一个。程序代码可(例如)储存于机器可读载体上。

其他实施例包括储存于机器可读载体上的用于执行本文中所描述的方法中的一个的计算机程序。

换言之，因此，本发明方法的实施例为具有程序代码的计算机程序，当计算机程序运行于计算机上时，该程序代码用于执行本文中所描述的方法中的一个。

因此，本发明方法的另一实施例为包括记录于其上的，用于执行本文中所描述的方法中的一个的计算机程序的数据载体(或数字存储介质，或计算机可读介质)。数据载体、数字存储介质或记录的介质通常为有形的和/或非暂时性的。

因此，本发明方法的另一实施例为表示用于执行本文中所描述的方法中的一个的计算机程序的数据流或信号序列。数据流或信号序列可例如用于经由数据通信连接(例如，经由因特网)而被传送。

另一实施例包括用于或适于执行本文中所描述的方法中的一个的处理构件，例如，计算机或可编程逻辑器件。

另一实施例包括安装有用于执行本文中所描述的方法中的一个的计算机程序的计算机。

根据本发明的另一实施例包含用以将用于执行本文中所描述的方法中的一个的计算机程序(例如电性或光学)传输到接收器的装置或系统。例如，接收器可为计算机、移动装置、存储器装置或类似。例如，此装置或系统可包含用于将计算机程序传输至接收器的文件服务器。

在一些实施例中，可编程逻辑器件(例如，现场可编程门阵列)可用于执行本文中所描述的方法的功能性中的一些或所有。在一些实施例中，现场可编程门阵列可与微处理器协作，以便执行本文中所描述的方法中的一个。大体而言，优选地由任何硬件装置执行这些方法。

以下将利用不同的措辞以及可助于阐明本发明背景的更多细节论述以上所述的教示。近来，范德蒙变换作为时频变换被提出，不同于离散傅立叶变换，范德蒙变换还对信号进行去相关。尽管傅立叶提供的近似或渐近去相关在一些情况下是足够的，其性能在利用短窗口的应用中是不足的。因此，在由于输入信号随时间迅速地改变而需要使用短分析窗口的语音和音频处理应用中，范德蒙变换将是有用的。此种应用常用在具有有限计算能力的移动设备上，由此高效的计算具有卓越的重要性。

然而，范德蒙变换的实施变成相当大的工作量：它要求其性能对于复杂度和准确率已被优化的先进数值计算工具。此贡献提供解决包括性能评估的此任务的基准方案。索引词-时频变换、去相关、范德蒙矩阵、托普利兹矩阵、翘曲离散傅立叶变换。

离散傅立叶变换为数字信号处理中的最基本手段中的一种。它提供频率分量形式的输入信号的物理激励再现。由于快速傅立叶变换(FFT)也以非常低的计算复杂度O(N log N)计算离散傅立叶变换，它已变成数字信号处理的最重要手段中的一种。

尽管有名的，离散傅立叶变换具有如此瑕疵：它未完全地对信号分量进行去相关(对于数值示例，参见部分4)。仅当变换长度收敛至无穷时，分量变成正交的。此近似去相关在许多应用中是足够良好的。然而，对于利用诸如许多语音和音频处理算法的相对小变换的应用，此近似的准确率限制算法的总体效率。例如，语音编码标准AMR-WB利用长为N＝64的窗口。实践已证明，离散傅立叶变换的性能在此情况下是不足的，且因而大多数主流语音编解码器使用时域编码。

图3c显示范德蒙变换的特征，由51标记的粗线示出信号的(非翘曲)傅立叶频谱，以及线52、53和54为利用输入信号进行滤波的、三个选中频率的带通滤波器的响应。范德蒙因子分解大小为64。

自然地，存在提供输入信号的去相关的大量变换，如卡洛南-洛伊(Karhunen-Loève)变换(KLT)。然而，KLT的分量为不具有像傅立叶变换一样简单的物理解释的抽象实体。另一方面，物理激励域允许物理激励标准简单明了地实施于处理方法中。因此期望提供物理解释和去相关二者的变换。

近来，我们已提出具有两种优选特征的被称为范德蒙变换的变换。它基于将埃尔米特托普利兹(HermitianToeplitz)矩阵分解为对角矩阵和范德蒙矩阵的乘积。此因子分解实际上也被称作协方差矩阵的卡拉西奥多礼(Carathéodory)参数化，且类似于汉克尔(Hankel)矩阵的范德蒙因子分解。

对于正定的埃尔米特托普利兹矩阵的特定情况，范德蒙因子分解将与频率-翘曲离散傅立叶变换相对应。换句话说，它是提供采样于并非必须均匀分布的频率处的信号分量的时频变换。范德蒙变换因此提供两种期望特性：去相关和物理解释。

当已分析地展示范德蒙变换的存在和特性时，当前工作的目的在于，首先，收集用于范德蒙变换的现有实际算法并形成文档。这些方法已在包括数值代数学、数值分析、系统识别、时频分析和信号处理的非常不同的领域中显现，由此它们常难以被发现。此文件因此是提供用于结果的分析和论述的联合平台的方法的回顾。其次，我们提供作为基准的数值示例以用于不同方法的性能的进一步评估。

此部分提供对范德蒙变换的简要介绍。对于关于应用的更全面的诱因和论述，请参考。

范德蒙矩阵V由标量vk定义为：

如果标量vk为不同的(对于)且它的逆具有显式公式，它是满秩的。

对称的托普利兹矩阵T由标量T_k定义为：

如果T为正定的，则它可被因子分解为：

T＝V^*∧V， (3z)

其中，∧为具有实数和严格正条目λ_kk＞0的对角矩阵，且指数级数V全部在单位圆v_k＝exp(iβ_k)上。此形式还被称为托普利兹矩阵的卡拉西奥多礼参数化。

在此我们提出范德蒙变换的两种使用：用作去相关变换或用作卷积矩阵的替代。首先考虑具有自相关矩阵E[xx^*]＝R_x的信号x。由于自相关矩阵是正定、对称的且是托普利兹，我们可将它因子分解为R＝V*∧V。由此得出结论，如果我们应用变换

y_d＝V^-*x (4z)

其中V^-*是V的逆埃尔米特，则y_d的自相关矩阵为

变换的信号y_d因此为不相关的。逆变换为

x＝V*y_d. (6z)

作为启发式描述，我们可说，正变换V^-*在其第k行包含滤波器，该滤波器的带通处于频率-β_k处且用于x的阻带输出具有低能量。具体地，输出的频谱形状接近于在单位圆上具有单极的AR滤波器的频谱形状。请注意，由于此滤波器组为信号自适应的，此处我们考虑滤波器的输出而非基本函数的频率响应。

反变换V^*反而在其列中具有指数级数，以使得x为指数级数的加权和。换句话说，变换为翘曲时频变换。图3c展示输入信号x的离散(非翘曲)傅立叶频谱以及V^-*的选中行的频率响应。

用于卷积域中的信号的评估的范德蒙变换可构造如下。令C为卷积矩阵且x为输入信号。考虑我们的目标为评估卷积信号y_c＝C_x的情况。例如，此评估在利用ACELP的语音编解码器中显现于在感知域中评估量化误差能量之处以及通过滤波描述至感知域的映射之处。

y_c的能量为：

||y_c||²＝||Cx||²＝x*C*Cx＝x*R_cx＝x*V*ΛVx＝||Λ^1/2Vx||² (7z)

y_c的能量因此等于变换且缩放的信号的能量：

y_v＝Λ^1/2Vx (8z)

因此，我们能等效地评估卷积或变换域中的信号能量||y_c||²＝||y_v||²。逆变换明显地为

x＝V^-1∧^-1/2y_v. (9z)

正变换V在其行中具有指数级数，由此它是翘曲傅立叶变换。它的逆V^-1在其列中具有在β_k处具有带通的滤波器。以此形式，滤波器组的频率响应等于离散傅立叶变换。它是利用常被看作为混叠分量以能够实现完美的重建的仅有的逆变换。

为了使用范德蒙变换，我们需要用于确定以及应用变换的高效算法。在此部分中，我们将论述可用的算法。让我们以变换的应用开始，因为它是更简单明了的任务。

V和V^＊的乘积是简单明了的，且可以复杂度O(N²)实施。为了减小存储需求，我们在此显示对于h＞1无需明确地评估指数的算法。即，如果y＝Vx且x的元素为ξ_k，则可利用循环确定y的元素η_k：

此处，T_h，k为临时标量，仅需要存储其当前值。对于N个分量，总体循环具有N个步骤，由此总体复杂度为O(N²)且存储需求为常量。对于y＝V*x可轻松地写出类似算法。

逆范德蒙矩阵V^-1和V^-*的乘积是稍微复杂的任务，但幸运的是，已可从文献中得到相对高效的方法。算法易于实施且对于x＝V^-1y和x＝V^-*y，复杂度为O(N²)且存储需求为线性的O(N)。然而，算法在每个步骤包括除法，这在许多架构中具有高常量代价。

尽管用于乘以逆的以上算法在分析的意义中是精确的，实际的实施对于大数N为数值上不稳定的。在我们的经验中，利用大小上达N～64的矩阵的计算有时是可能的，但除此之外，数值不稳定性致使这些算法就其本身而言是无用的。实际的方案为根V_k的Leja-排序，其相当于利用部分主元消元的高斯消元法。Leja-排序的主要思想为以根V_k距前面的0...(k-1)的根的距离被最大化的方式对根进行重排序。通过此重排序，显现于算法中的分母被最大化且中间变量的值被最小化，由此截断误差的贡献也被最小化。Leja-排序的实施是简单的且可以以复杂度O(N²)和存储需求O(N)实现。

然后，最终障碍是获得因子分解，即，根V_k以及需要时的对角线值λ_kk。就我们所知，可通过求解

Ra＝[11...1]^T， (11z)

获得根。其中，a具有元素α_k。然后v₀＝1和剩余根V₁...V_N为多项式的根。我们可轻松地显示，这相当于求解汉克尔系统

其中，然后根V_k为的根。

由于原始托普利兹系统的因子分解等式(11z)与等式(12z)等效，我们可使用用于汉克尔矩阵的因子分解的快速算法。此算法返回三对角矩阵，其特征值与的根相对应。然后可以通过应用LR算法以O(N²)或通过标准的非对称QR算法以O(N²)获得特征值。此种方式获得的根为近似值，由此它们可能会稍微脱离单位圆。然后，将根的绝对值归一化至统一单位并利用牛顿方法的2或3次迭代进行精炼是有用的。完整的过程具有O(N²)的计算代价。

因子分解中的最后步骤为获得对角线值∧。请观察，

Re＝V*∧Ve＝V*λ (13z)

其中，e＝[10...0]^T且λ为包含∧的对角线值的向量。换句话说，通过计算

λ＝V^-*(Re)， (14z)

我们获得对角线值λ_kk。利用以上论述的方法可计算此逆，由此以复杂度O(N²)获得对角线值。

总之，矩阵R的因子分解所需的步骤为：

1、使用莱文森一德宾(Levinson-Durbin)或其他经典方法，求解等式(11z)。

2、通过扩展自相关序列。

3、对序列T_k应用三对角化算法。

4、使用LR或对称的QR算法，求解特征值vk。

5、通过将v_k缩放至统一单位以及牛顿方法的数次迭代，对根的位置进行精炼。

6、使用等式(14z)确定对角线值λ_kk。

让我们以展示所使用的概念的数值示例开始。此处，矩阵C为与简单滤波器1+z^-1相对应的卷积矩阵，矩阵R为它的自相关，矩阵V为利用部分3中的算法获得的对应范德蒙矩阵，矩阵F为离散傅立叶变换矩阵且矩阵∧_V和∧_F展示两个变换的对角化准确率。因此，我们可定义

由此我们可利用

评估对角化。

此处，我们可看到，利用范德蒙变换，我们获得完美地对角化的矩阵∧_V。离散傅立叶变换的性能远非最优的，因为对角线外的值明显地是非零。作为性能的度量，我们可计算对角线外的值的绝对和与对角线上的值的绝对和之比，其对于范德蒙因子分解为0，而对于傅立叶变换为0.444。

然后，我们可进行对部分3中描述的实施的评估。在提供性能基准的目的下，我们已在MATLAB中实施每个算法，基于该性能基准，未来的工作可进行对比并找到最终的性能瓶颈。我们将考虑关于复杂度和准确率的性能。

为了确定因子分解的性能，我们将范德蒙因子分解与离散傅立叶和卡洛南-洛伊变换进行对比，利用特征值分解应用后者。我们已使用两种方式应用范德蒙因子分解，第一，在此论文中描述的算法(V₁)以及第二，在使用由MATLAB提供的内置寻根函数(V₂)中描述的方法。由于此MATLAB函数为经细致调整的一般算法，我们预期将以比我们为特定目的而创建的算法高的复杂度获得准确的结果。

作为用于我们的实验的数据，我们使用以12.8kHz的采样率用于MPEG USAC标准的评估中的语音、音频和混合音样本的集合。利用汉明窗口，对音频样本加窗至期望长度，并计算它们的自相关。为了确保自相关矩阵为正定的，主对角线乘以(1+10^-5)。

对于性能度量，我们使用关于归一化运行时间的计算复杂度和关于由对角线外的元素的绝对和与对角线上的元素的绝对和之比度量的距对角矩阵有多近的准确率。结果被列出在表1和2中。

表1、关于归一化运行时间的因子分解算法对于不同窗口长度N的复杂度

表2、关于的对角线外的值的绝对和与对角线上的值的绝对和之比的log₁₀的因子分解算法对于不同窗口长度N的准确率

请注意，此处，对比算法之间的运行时间是不明智的，仅是作为帧大小的函数的复杂度的增大，因为内置MATLAB函数已以不同于我们自己算法的语言实施。我们可看到，所提议的算法V₁的复杂度随可比拟于KLT的比率增大，而应用MATLAB的寻根函数V₂的算法增大更多。所提议的因子分解算法V₁的准确率尚非最优的。然而，由于MATLAB的寻根函数V₂引致可比拟于KLT的准确率，我们得到结论，通过算法改进的改进是可能的。

第二个实验是变换的应用以确定准确率和复杂度。首先，我们应用等式(4z)和(9z)，其复杂度在表3中列出。此处，我们可看到，KLT的矩阵乘法以及MATLAB的矩阵系统的内置方案V₂具有大体相同的复杂度增大比率，而用于等式(4z)和(9z)的所提议的方法具有更小的增大。自然地，FFT快于所有其他方法。

最后，为了获得范德蒙方案的准确率，我们依次应用正变换和反变换。在表4中列出了原始向量和重构建向量之间的欧氏(Euclidean)距离。我们可观察到，首先，正如所预期的，FFT和KLT算法为最准确的，因为它们基于正交变换。其次，我们可看到，所提议的算法V₁的准确率稍微低于MATLAB的内置方案V₂，但两个算法均提供足够的准确率。

我们已在回顾可用算法以及提供用于进一步开发的性能基准的目的下，提出使用范德蒙因子分解对时频变换进行去相关的实施细节。而原则上可从先前工作得到算法，它结果是使得系统按需求运行。

表3、关于归一化运行时间的范德蒙方案对于不同的窗口长度N的复杂度。此处，v₁^-*和V₁^-1预示利用各个所提议的算法的等式(4z)和(9z)的方案。

表4、如通过测量的正变换和反变换的准确率，其中x和为原始向量和重构建向量。

相当大的工作量。主要挑战为数值准确率和计算复杂度。实验证实，可得到以O(N2)复杂度的方法，尽管获得低复杂度同时具有数值稳定性是个挑战。然而，由于一般MATLAB实施提供准确的方案，我们断定利用实施的进一步调整，获得高准确率是可能的。

总之，我们的实验显示，对于范德蒙方案，所提议的算法具有良好的准确率和足够低的复杂度。对于因子分解，为特定目的而创建的因子分解的确以合理的复杂度给出比FFT更优的去相关，而对于准确率，仍存在改进空间。MATLAB的内置实施给出令人满意的准确率，这将我们引向如此结论：可实施准确的O(N²)算法。

上文所描述的实施例仅仅说明本发明的原理。应理解，对本文中所描述的配置及细节的修改及变型对本领域技术人员而言将是显而易见。因此，仅意欲由待决专利的权利要求的范围限制，而不由通过本文的实施例的描述及解释而提出的特定细节限制。

参考文献

[1]B.Bessette，R.Salami，R.Lefebvre，M.Jelinek，J.Rotola-Pukkila，J.Vainio，H.Mikkola，and K.“The adaptive multirate wideband speech codec(AMR-WB)，″Speech and Audio Processing，IEEE Transactions on，vol.10，no.8，pp.620-636，2002.

[2]ITU-T G.718，“Frame error robust narrow-band and wideband embedded variable bit-rate coding of speech and audio from8-32kbit/s，″2008.

[3]M.Neuendorf，P.Gournay，M.Multrus，J.Lecomte，B.Bessette，R.Geiger，S.Bayer，G.Fuchs，J.Hilpert，N.Rettelbach，R.Salami，G.Schuller，R.Lefebvre，and B.Grill，“Unied speech and audio coding scheme forhigh quality at low bitrates，″in Acoustics，Speech and Signal Processing.ICASSP 2009.IEEE Int Conf，2009，pp.1-4，

[4]J.-P.Adoul，P.Mabilleau，M.Delprat，and S.Morissette，“Fast CELP coding based on algebraic codes，″in Acoustics，Speech，and Signal Processing，IEEE International Conference on ICASSP′87.，vol.12.IEEE，1987，pp.1957-1960.

[5]C.Laamme，J.Adoul，H.Su，and S.Morissette，“On reducing computational complexity of codebook search in CELP coder through the use of algebraic codes，″in Acoustics，Speech，and Signal Processing，1990.ICASSP-90.，1990International Conference on.IEEE，1990，pp.177-180.

[6]F.-K.Chen and J.-F.Yang，“Maximum-take-precedence ACELP：a low complexity search method，″in Acoustics，Speech，and Signal Processing，2001.Proceedings.(ICASSP′01).2001 IEEE International Conference on，vol.2.IEEE，2001，pp.693-696.

[7]K.J.Byun，H.B.Jung，M.Hahn，and K.S.Kim，“A fast ACELP codebook search method，″in Signal Processing，2002 6th International Conference on，vol.1.IEEE，2002，pp.422-425.[8]N.K.Ha，\A fast search method of algebraic codebook by reordering search sequence，″in Acoustics，Speech，and Signal Processing，1999.Proceedings.，1999 IEEE International Conference on，vol.1.IEEE，1999，pp.21-24.

[9]M.A.Ramirez and M.Gerken，“Efficient algebraic multipulse search，″in Telecommunications Symposium，1998.ITS′98 Proceedings.SBT/IEEE International.IEEE，1998，pp.231-236.

[10]T.“Computationally efficient objective function for algebraic codebook optimization in ACELP，″in Interspeech 2013，August 2013.

[11]|“Vandermonde factorization of Toeplitz matrices and applications in filtering and warping，″IEEE Trans.Signal Process.，vol.61，no.24，pp.6257-6263，2013.

[12]G.H.Golub and C.F.van Loan，Matrix Computations，3rd ed.John Hopkins University Press，1996.

[13]T.J.Fischer，and D.Boley，“Implementation and evaluation of the Vandermonde transform，″in submitted to EUSIPCO 2014(22^nd European Signal Processing Conference 2014)(EUSIPCO 2014)，Lisbon，Portugal，Sep.2014.

[14]T.G.Fuchs，M.Multrus，and M.Dietz，“Linear prediction based audio coding using improved probability distribution estimation，″US Provisional Patent US 61/665 485，6，2013.

[15]K.Hermus，P.Wambacq et al.，\A review of signal subspace speech enhancement and its application to noise robust speech recognition，″EURASIP Journal on Applied Signal Processing，vol.2007，no.1，pp.195-195，2007.