道路交通工具行驶控制方法和装置与流程

本发明涉及道路交通信息技术领域，特别是涉及行驶控制领域，尤其涉及一种道路交通工具行驶控制方法和装置。

背景技术：

随着道路交通工具的普及以及互联网技术的发展，道路交通工具行驶控制成为一种新的需求，可用于导航提示或者无人驾驶等。目前道路交通工具行驶控制主要是通过计算机视觉识别出障碍物，并基于地图数据所记载的道路信息规划行车路线，从而依据规划的行车路线进行行驶控制。

然而，目前的道路交通工具行驶控制方式，依赖于地图数据所记载的道路信息，而地图数据的更新是滞后的，当道路信息发生改变时并不能及时更新，这就导致无法准确地进行行驶控制；而且还会带来驾驶安全问题，尤其是应用于无人驾驶时问题更为严重。

技术实现要素：

基于此，有必要针对目前的道路交通工具行驶控制方式依赖于地图数据导致行驶控制不准确的问题，提供一种道路交通工具行驶控制方法和装置。

一种道路交通工具行驶控制方法，所述方法包括：

获取道路交通环境的实时感知结果；

根据所述实时感知结果得到多种道路元素相应的当前道路元素参数；

根据因子图模型和所述当前道路元素参数预测道路场景参数；所述因子图模型用于表达道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数；

根据预测的道路场景参数生成行驶控制指令并输出。

一种道路交通工具行驶控制装置，所述装置包括：

数据获取模块，用于获取道路交通环境的实时感知结果；根据所述实时感知结果得到多种道路元素相应的当前道路元素参数；

预测模块，用于根据因子图模型和所述当前道路元素参数预测道路场景参数；所述因子图模型用于表达道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数；

输出模块，用于根据预测的道路场景参数生成行驶控制指令并输出。

上述道路交通工具行驶控制方法和装置，利用实时感知结果的当前道路元素参数来预测道路场景参数，从而根据预测的道路场景参数来进行行驶控制，不再依赖于地图数据，交通工具行驶控制的准确性得以增强。而且，通过因子图来表达道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数，因子图用图结构描述全局目标函数的因式分解形式，将大规划的全局运算划分为简单的局部运算，提高了行驶控制的效率。再者，通过因子图模型可以将多种道路元素融合，可以考虑到道路元素参数之间的相关性，而不是假设彼此独立，使得交通工具行驶控制符合真实道路场景，控制准确。

附图说明

图1为一个实施例中道路交通工具行驶控制系统的应用环境图；

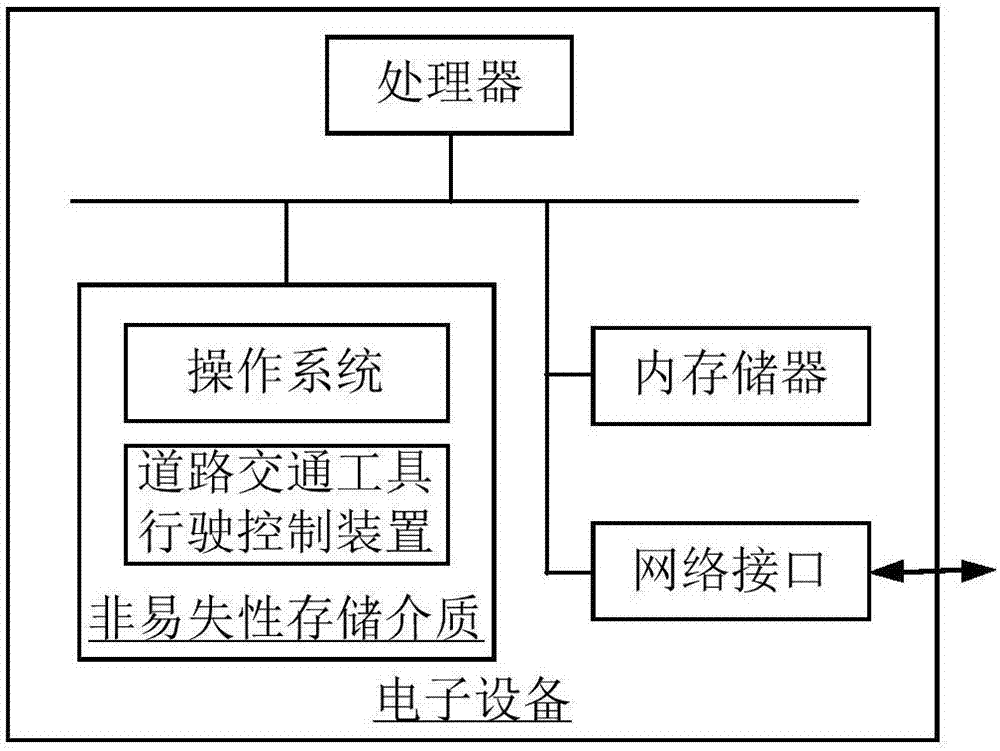
图2为一个实施例中电子设备的内部结构示意图；

图3为一个实施例中道路交通工具行驶控制方法的流程示意图；

图4为一个实施例中训练因子图模型的步骤的流程示意图；

图5为一个实施例中将复合概率图模型转化为因子图模型的过程示意图；

图6为一个实施例中因子图模型的建模、学习及推理过程示意图；

图7为一个实施例中因子图模型的结构学习过程示意图；

图8为一个实施例中道路交通工具行驶控制装置的结构框图；

图9为另一个实施例中道路交通工具行驶控制装置的结构框图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

图1为一个实施例中道路交通工具行驶控制系统的应用环境图，该系统包括感知设备110、电子设备120和道路交通工具130。其中感知设备110可以是摄像头或者雷达；电子设备120可以置于交通工具130内部直接控制交通工具130，也可以是通过网络远程向交通工具130发送行驶控制指令。道路交通工具130是可沿道路行驶的交通工具，比如小汽车、货车、客车、摩托车或者电动自行车等。

图2为一个实施例中电子设备120的内部结构示意图。如图2所示，该电子设备包括通过系统总线连接的处理器、非易失性存储介质、内存储器和网络接口。其中，电子设备的非易失性存储介质存储有操作系统，还包括一种道路交通工具行驶控制装置，该道路交通工具行驶控制装置用于实现一种道路交通工具行驶控制方法。电子设备的处理器用于提供计算和控制能力，支撑电子设备的运行。电子设备的内存储器为非易失性存储介质中的道路交通工具行驶控制装置提供运行环境。该内存储器中可存储有计算机可读指令，该计算机可读指令被处理器执行时，可使得处理器执行一种道路交通工具行驶控制方法。网络接口用于连接到网络。该电子设备可以是手机、车载电脑或者服务器等。本领域技术人员可以理解，图2中示出的结构，仅仅是与本申请方案相关的部分结构的框图，并不构成对本申请方案所应用于其上的电子设备的限定，具体的电子设备可以包括比图中所示更多或更少的部件，或者组合某些部件，或者具有不同的部件布置。

如图3所示，在一个实施例中，提供了一种道路交通工具行驶控制方法，本实施例以该方法应用于上述图1和图2中的电子设备120来举例说明。该方法具体包括如下步骤：

步骤302，获取道路交通环境的实时感知结果。

道路交通环境是指道路交通工具行驶时所处的环境，实时感知结果则是通过感知设备实时感知的用于描述道路交通环境中的道路元素的数据。电子设备 可通过感知设备采集道路交通环境的图像，对道路交通环境进行语义分割，区分出各种道路元素，得到实时感知结果。

实时感知结果包括道路信息，还可以包括交通标志信息、车辆信息、行人信息以及场景光流等中的至少一种。其中，道路信息可包括车道线信息和道路灭点信息。车道线是道路路面上用于对道路交通工具的行驶进行指示的形状规则的线状标示，车道线信息比如车道线位置或车道线类型或车道线所属道路。道路灭点是道路在远处消失的点，道路灭点以上一般是天空部分，道路灭点信息比如道路灭点位置或者道路灭点所属的道路。

进一步地，车辆和行人是道路交通环境中的动态道路元素，可采用目标跟踪方式得到车辆信息和/或行人信息。车辆信息比如行驶速度、行驶方向、车辆位置以及车辆所在道路等，行人信息比如行走速度、行走方向、行人位置以及行人所在道路等。场景光流也可以表达道路交通环境中运动目标的信息。

步骤304，根据实时感知结果得到多种道路元素相应的当前道路元素参数。

其中，道路元素是指道路交通环境中对道路交通工具在道路上行驶状态造成影响的因素，比如车道线、道路灭点、交通标志、车辆或者行人等。道路元素参数是将相应道路元素的感知结果参数化表达后得到的表征该道路元素特征的参数。在一个实施例中，道路元素参数包括车辆跟踪参数、行人跟踪参数、车道线检测结果、道路灭点检测结果以及交通标志检测结果中的至少一种。这里将实时感知结果参数化为相应道路元素在当前的道路元素参数。多种道路元素的种类数是确定的。

步骤306，根据因子图模型和当前道路元素参数预测道路场景参数；因子图模型用于表达道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数。

其中，因子图是贝叶斯网络和马尔科夫网络的统一表示，通过引入因子节点来明确地描述因子图上联合概率分布的分解。进一步地，因子图引入了一个因子节点集合，相当于定义在通常节点子集上的目标函数。因子图是一个二部图，用来描述某个变量集上的局部函数的乘积。

因子图模型是采用因子图的原理训练得到的数学模型，表达了道路场景参 数和多种道路元素相应的道路元素参数间的联合分布概率密度函数，电子设备根据该联合分布概率密度函数以及当前道路元素参数，估计道路场景参数取值的概率，从而将概率最大的取值作为预测的道路场景参数。估计道路场景参数取值的概率时可采用最大后验概率估计方法(map)或者最大似然估计方法。

道路场景参数是对道路交通工具进行行驶控制时所依据的参数，在一个实施例中，道路场景参数包括道路拓扑关系、路口中心位置、道路宽度、即将驶入的道路与车头方向夹角以及当前道路与即将驶入的道路之间的夹角中的至少一种。其中道路拓扑关系比如直行道路、左转道路、右转道路、t型道路或者十字路口等。路口中心位置可以是路口中心在车体坐标系下的坐标。

在一个实施例中，因子图模型所表达的道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数即目标函数可用如下公式(1)表示：

其中，θ表示因子图模型中的所有参数。r＝{k,c,w,r,a}表示道路场景参数，是用来描述道路拓扑关系和几何结构的随机变量；其中k表示道路拓扑关系，c＝(x,z)表示路口中心在车体坐标系下的坐标，w表示道路宽度，r表示即将驶入的道路与车头方向夹角，a表示当前道路与即将驶入的道路之间的夹角。

t＝{t1,...,tnt}表示车辆跟踪参数，共有nt个参数；p＝{p1,...,pnp}表示行人跟踪参数，共有np个参数；l＝{l1,...,lnl}表示道路灭点检测结果，共有nl个参数；v＝{v1,...,vnv}表示车道线检测结果，共有nv个参数；s＝{s1,...,sns}表示交通标志检测结果，共有ns个参数。e＝{t,p,l,v,s}构成因子图模型的观测变量，也叫作数据证据。{e-t}是集合{p,l,v,s}的简化表达，类似的，{e-p}表示集合{t,l,v,s，}{e-l}表示集合{t,p,v,s}，{e-v}表示集合{t,p,l,s}，{e-s}表示集合{t,p,l,v}。

在一个实施例中，电子设备具体可以根据以下公式(2)采用最大后验概率估计方法预测道路场景参数r：

r＝argmaxrp(r|e,θ)公式(2)

其中，这里e表示当前道路元素参数，θ表示因子图模型中的所有参数，r表示预测的道路场景参数，公式(2)表示预测的道路场景参数r使得概率p(r|e,θ)最大化。

步骤308，根据预测的道路场景参数生成行驶控制指令并输出。

其中，行驶控制指令是可控制道路交通工具行驶的指令，比如控制道路交通工具的行驶方向、行驶速度或者刹车等。电子设备可直接将行驶控制指令输出给道路交通工具的控制器，使得道路交通工具实现自动驾驶；电子设备也可以将行驶控制指令以可视提示方式或者语音播放方式输出，比如提示改变行驶方向、提示改变行驶速度或者提示刹车等，以实现道路交通工具的导航。

上述道路交通工具行驶控制方法，利用实时感知结果的当前道路元素参数来预测道路场景参数，从而根据预测的道路场景参数来进行行驶控制，不再依赖于地图数据，交通工具行驶控制的准确性得以增强。而且，通过因子图来表达道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数，因子图用图结构描述全局目标函数的因式分解形式，将大规划的全局运算划分为简单的局部运算，提高了行驶控制的效率。再者，通过因子图模型可以将多种道路元素融合，可以考虑到道路元素参数之间的相关性，而不是假设彼此独立，使得交通工具行驶控制符合真实道路场景，控制准确。

在一个实施例中，道路元素参数包括跟踪目标参数；该方法还包括：根据因子图模型和预测的道路场景参数预测跟踪目标相对于道路位置；步骤308包括：根据预测的道路场景参数和预测的跟踪目标相对于道路位置生成行驶控制指令并输出。

其中，跟踪目标比如车辆或者行人等运动目标，跟踪目标参数比如上述的车辆跟踪参数t或者行人跟踪参数p。跟踪目标相对于道路位置是指车辆或者行人等跟踪目标相对于道路的位置关系。根据预测的道路目标相对于道路位置，电子设备可确定行驶的道路上存在的障碍物，与预测的道路场景参数结合，便可以确定可行的行进路线，从而生成相应的行驶控制指令并输出。

在一个实施例中，电子设备具体可以根据以下公式(3)采用最大后验概率估计方法预测车辆在道路中的位置：

其中，l表示当前所在道路的标识，lnt表示车辆tnt所在道路的标识，snt表示车辆跟踪参数中的车辆位置的样条模型的表达；t表示当前车辆的车辆跟踪参数；r表示预测的道路场景参数；vl表示预测得到的车辆在道路中的位置的集合；vl表示预测的各个追踪车辆在道路中的位置。对于行人也可以采用相同的方法求得行人在道路中的位置，具体将公式(3)中跟踪车辆的信息替换为跟踪行人的信息。

本实施例中，通过预测跟踪目标相对于道路位置，在生成行驶控制指令时不仅考虑预测的道路场景参数，还会考虑预测的跟踪目标相对于道路位置，这样可以使得道路交通工具行驶更加智能化，应用于无人驾驶场景时会更加安全。

如图4所示，在一个实施例中，在步骤302之前，该道路交通工具行驶控制方法还包括训练因子图模型的步骤，具体包括如下步骤：

步骤402，将多种道路元素进行参数化表达，得到相应的道路元素参数。

电子设备将各种道路元素进行坐标系的统一以及参数化表达，得到相应的道路元素参数。具体对于车道线可采用通过若干点的样条模型表达，将样条模型表达中的参数作为车道线相应的道路元素参数。道路灭点的道路元素参数可采用道路灭点在道路鸟瞰图中的坐标位置。交通标志的道路元素参数可采用交通标志的位置及其语义表示。行人和车辆等跟踪目标是动态数据，可采用每一帧视频图像中跟踪目标的位置及其跟踪模型的参数作为跟踪目标的道路元素参数。

步骤404，根据各道路元素对应的道路元素参数分别构建概率图模型。

具体地，由于道路交通环境中存在静态的道路元素，比如车道线或者交通标志；也存在动态的道路元素，比如光流、行人或者车辆，这里对于静态和动态的道路元素可分别采用不同类型的概率图模型建模。具体对于静态的道路元素可采用贝叶斯网络(bn)模型建立概率图模型，对于动态的道路元素可采用隐马尔科夫(hmm)模型或者多重参考(mrf)模型建立概率图模型。

步骤406，根据道路交通先验知识将各概率图模型连接，得到因子图模型。

其中，道路交通先验知识是已知的在道路交通环境中存在的信息，比如红灯时车辆多数减速或者停车，道路路口处车辆速度较慢，车辆在左侧道路超车，行人在道路两旁，两辆车不可能在相同位置等。道路交通先验知识可以反映出各个道路元素参数之间的关联，因此可利用交通先验知识，将各概率图模型连接中相关联的节点连接，并标记相应的概率，从而将各概率图模型统一起来形成复合概率图模型。电子设备根据因子图的表达规则，将复合概率图模型重表达，以将有向图模式的概率图模型转化为无向图模式的因子图模型。如图5所示，将复合概率图模型中的贝叶斯网络模型和隐马尔科夫模型分别进行因子图表达，得到因子图模型。

概率图模型是对复杂不确定性问题进行建模、推理的重要工具之一，常用的概率图模型主要包括贝叶斯网络模型、马尔科夫网络模型以及因子图模型等。其中因子图模型是一种表示多元函数因式分解结构的二分图，具有很强的表达能力。因子图模型不仅可以表示贝叶斯网络模型和马尔科夫网络模型所能够表示的所有独立性关系，还能够表示她们所不能表示的独立性关系。而且，贝叶斯网络模型和马尔科夫网络模型只需经过简单的步骤就可以转化为因子图模型。

步骤408，根据道路数据样本训练因子图模型。

具体地，因子图模型的训练包括结构学习和参数学习。结构学习包括确定因子图模型的节点和边，以及节点与边的连接方式，以及是否存在反馈回路等。电子设备可根据标记道路数据样本进行各种道路场景下的道路场景参数及相应道路元素参数之间的依赖性聚类分析，确定因子图模型中存在关联的因子，从而学习因子图模型的结构，将层次因子图模型转化为标准因子图。进而通过一些bp(errorbackpropagation,误差反向传播)算法学习因子图模型中的参数。

其中道路数据样本可以是标记道路数据样本，标记道路数据样本是已标注预测结果和观测变量的样本。依赖性聚类分析具体可依据欧氏距离或者马氏距离通过聚类算法(如k-means等非监督方法)进行聚类分析。层次因子图模型是在标准因子图模型基础上增加了有关复合变量和复合因子，其中复合变量和 复合因子是在建模过程中可获得的中间结果，将层次因子图模型转化为标准因子图模型，可使得建模过程更加条理有序，也可以简化因子图模型的推理过程。

对因子图模型的参数学习，具体可采用置信传播(beliefpropagation)机制利用和积算法(sum-productalgorithm)。和积算法是常用的因子图模型推理算法，采用和积算法训练因子图模型时，通过在因子图模型相邻结点间进行消息传递来实现边缘概率分布函数的计算，边缘概率是指某一组概率的加和。

在一个实施例中，电子设备可根据道路数据样本载入根据道路交通先验知识得到的先验的因子图模型，采用置信传播机制并利用和积算法进行边缘概率分布函数的计算，并验证因子图模型中节点之间的依赖关系，根据依赖关系进行减枝，逐步形成一个标准因子图模型，实现因子图模型的结构学习，进而根据道路数据样本进行参数学习。

具体地，电子设备可对因子图模型的两两道路元素的相应道路元素参数的节点，比如交通标志和车辆，道路和行人等，进行依赖关系的分析，这种依赖关系表示节点之间的相关性。如果因子间关系比较小就直接切掉因子图模型中相应节点之间的边关联。对因子图模型进行结构学习时可构建因子图模型的观测变量和关联矩阵的代价函数，通过求取最小代价函数求得关联矩阵，从而根据关联矩阵进行减枝，其中关联矩阵表示因子图模型中节点之间的依赖关系。求取最小化代价函数是一个np-hard(非确定性多项式困难)问题，可采用模拟退火方式实现。

本实施例中，将各种道路元素进行参数化表达得到道路元素参数并构建概率图模型，根据道路交通先验知识将概率图模型连接得到因子图模型，可得到符合道路交通先验知识的因子图模型，进而利用道路数据样本训练因子图模型，可使得因子图模型能够准确描述道路交通环境，使得电子设备可准确理解道路交通环境，进而准确地对道路交通工具的行驶进行控制。

在一个实施例中，道路数据样本包括标记道路数据样本和未标记道路数据样本；步骤408具体包括：根据标记道路数据样本和未标记道路数据样本，采用半监督学习方式对因子图模型进行结构学习和参数学习。

未标记道路数据样本是指仅标记观测变量而未标记预测结果的样本。电子 设备可先确定标记道路数据样本和未标记道路数据样本的相似度，从而根据标记道路数据样本所标注的预测结果来估计未标记道路数据样本的预测结果，进而根据标记道路数据样本、未标记道路数据样本及估计的预测结果对因子图模型进行结构学习和参数学习。计算相似度可考虑多种相似度，比如道路形态相似度、场景结构相似度以及语义相似度等，还可以将车道线与可行驶区域探测结果融合，建立道路及车道线形态样本特征字典，从而根据车道线形态样本特征字典中的特征矢量来度量相似度。

本实施例中，通过半监督学习方式训练因子图模型，可减少标注代价，提高因子图模型的训练效率。

在一个实施例中，因子图模型是动态的；该道路交通工具行驶控制方法还包括：收集实时感知结果；根据收集的实时感知结果更新因子图模型。具体地，电子设备可收集实时感知结果以及相应的预测结果作为标注道路数据样本，或者收集实时感知结果作为未标注道路数据样本，进一步对因子图模型进行结构学习和/或参数学习。电子设备还可以基于大规模稀疏矩阵对因子图模型进行优化。通过不断更新因子图模型，可以保持因子图模型用于道路交通工具行驶控制的准确性。

在一个具体的应用场景中，道路交通工具行驶控制方法的整个流程如图6所示。电子设备收集参与道路交通环境的各种道路元素的实时感知结果，实时感知结果可通过视觉系统或雷达系统等感知设备感知得到。各种道路元素比如车道线、道路灭点、交通标志、行人、车辆等，实时感知结果如车道线检测结果、道路灭点检测结果、交通标志检测结果及其语义、行人跟踪器的参数以及车辆跟踪器的参数等。通过语义分割可识别各种道路元素。

进一步地，电子设备将实时感知结果进行参数化表达，得到道路元素参数；根据各道路元素对应的道路元素参数分别构建概率图模型；根据道路交通先验知识将各概率图模型连接，得到复合概率图模型，将复合概率图模型转化为动态因子图。将道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数作为目标函数。

进一步地，电子设备基于时间和空间的关联性，根据实时感知结果并采用 半监督学习方式对因子图模型进行结构学习和参数学习，其中结构学习过程如图7所示。利用更新的增量数据动态更新因子图模型，并利用大规模稀疏矩阵优化因子图模型。最终可采用例如metropolis-hastings算法的mcmc(markovchainmontecarlo，随机模拟)算法来实现参数推理，如预测道路场景参数。

如图8所示，在一个实施例中，提供了一种道路交通工具行驶控制装置800，包括：数据获取模块801、预测模块802和输出模块803。

数据获取模块801，用于获取道路交通环境的实时感知结果；根据实时感知结果得到多种道路元素相应的当前道路元素参数。

预测模块802，用于根据因子图模型和当前道路元素参数预测道路场景参数；因子图模型用于表达道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数。

输出模块803，用于根据预测的道路场景参数生成行驶控制指令并输出。

上述道路交通工具行驶控制装置800，利用实时感知结果的当前道路元素参数来预测道路场景参数，从而根据预测的道路场景参数来进行行驶控制，不再依赖于地图数据，交通工具行驶控制的准确性得以增强。而且，通过因子图来表达道路场景参数和多种道路元素相应的道路元素参数间的联合分布概率密度函数，因子图用图结构描述全局目标函数的因式分解形式，将大规划的全局运算划分为简单的局部运算，提高了行驶控制的效率。再者，通过因子图模型可以将多种道路元素融合，可以考虑到道路元素参数之间的相关性，而不是假设彼此独立，使得交通工具行驶控制符合真实道路场景，控制准确。

在一个实施例中，预测模块802还用于根据因子图模型和预测的道路场景参数预测跟踪目标相对于道路位置。输出模块803还用于根据预测的道路场景参数和预测的跟踪目标相对于道路位置生成行驶控制指令并输出。

本实施例中，通过预测跟踪目标相对于道路位置，在生成行驶控制指令时不仅考虑预测的道路场景参数，还会考虑预测的跟踪目标相对于道路位置，这样可以使得道路交通工具行驶更加智能化，应用于无人驾驶场景时会更加安全。

如图9所示，在一个实施例中，道路交通工具行驶控制装置800还包括： 因子图模型训练模块804，用于将多种道路元素进行参数化表达，得到相应的道路元素参数；根据各道路元素对应的道路元素参数分别构建概率图模型；根据道路交通先验知识将各概率图模型连接，得到因子图模型；根据道路数据样本训练因子图模型。

本实施例中，将各种道路元素进行参数化表达得到道路元素参数并构建概率图模型，根据道路交通先验知识将概率图模型连接得到因子图模型，可得到符合道路交通先验知识的因子图模型，进而利用道路数据样本训练因子图模型，可使得因子图模型能够准确描述道路交通环境，使得电子设备可准确理解道路交通环境，进而准确地对道路交通工具的行驶进行控制。

在一个实施例中，道路数据样本包括标记道路数据样本和未标记道路数据样本；因子图模型训练模块804还用于根据标记道路数据样本和未标记道路数据样本，采用半监督学习方式对因子图模型进行结构学习和参数学习。

本实施例中，通过半监督学习方式训练因子图模型，可减少标注代价，提高因子图模型的训练效率。

在一个实施例中，道路交通工具行驶控制装置800还包括：因子图模型更新模块805，用于收集实时感知结果；根据收集的实时感知结果更新因子图模型。

在一个实施例中，道路场景参数包括道路拓扑关系、路口中心位置、道路宽度、即将驶入的道路与车头方向夹角以及当前道路与即将驶入的道路之间的夹角中的至少一种；道路元素参数包括车辆跟踪参数、行人跟踪参数、车道线检测结果、道路灭点检测结果以及交通标志检测结果中的至少一种。

本领域普通技术人员可以理解实现上述实施例方法中的全部或部分流程，是可以通过计算机程序来指令相关的硬件来完成，该计算机程序可存储于一计算机可读取存储介质中，该程序在执行时，可包括如上述各方法的实施例的流程。其中，前述的存储介质可为磁碟、光盘、只读存储记忆体(read-onlymemory，rom)等非易失性存储介质，或随机存储记忆体(randomaccessmemory，ram)等。

以上实施例的各技术特征可以进行任意的组合，为使描述简洁，未对上述实施例中的各个技术特征所有可能的组合都进行描述，然而，只要这些技术特征的组合不存在矛盾，都应当认为是本说明书记载的范围。

以上实施例仅表达了本发明的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。因此，本发明专利的保护范围应以所附权利要求为准。