一种基于板簧形变的罐车整车质量动态估计方法与流程

[0001]
本发明涉及一种罐车质量动态估计方法，具体的是一种基于板簧形变的罐车整车质量动态估计方法，属于车载估计技术领域。


背景技术：

[0002]
近年来，由于装载量大、运输效率高，罐车的使用越来越多，人们对于罐车的需求不再简单局限于运输工具的范畴，对其运行效率、行驶稳定性和主动安全性等的追求越来越高，故驾驶辅助电子系统广泛运用于罐车上，如制动防抱死系统(abs)、车身电子稳定系统(esp)等。这些电子系统大多是根据罐车行驶状态参数进行工作的，其中整车质量是一个关键参数，然而罐车容积大，整车质量随着装载货物种类和体积的不同而经常变化，因此准确实时估计整车质量对上述电子系统自适应调整其控制算法具有重要意义。同时罐车装载状态异常是导致车辆发生事故主要原因之一，我国每年由于此类原因引发的交通事故占罐车交通事故的60％以上，而对罐车整车质量的动态估计是避免此类事故的有效方法。
[0003]
现有的整车质量估计方法主要是基于车辆纵向动力学模型实现整车质量的动态估计，这些方法将车辆的速度、加速度和发动机扭矩等信息带入模型从而估算出整车质量，如青岛大学臧政等人利用车辆发动机扭矩作为动力学模型输入估算整车质量(臧政,霍炜,王玉海,李兴坤,郑旭光,李圆圆.重型商用车辆质量估计算法研究[j].中国机械工程)。然而建立的动力学模型复杂，工程化困难，并且大多数方法是通过多维仿真试验来验证其算法的有效性，未对算法进行实车道路测试；并且，在估计罐车整车质量时，由于受液体扰动的影响，罐车质心位置运动多变，给模型估算带来一定的误差。


技术实现要素：

[0004]
基于现状，针对使用钢板弹簧悬架的罐车，本发明提出了一种基于板簧形变的罐车整车质量动态估计方法，该方法首先明确用于估计整车质量的参数及其获取方式，然后设计罐车典型行驶场景并开展实车试验获得样本信息，接着利用ls-svm拟合电阻应变片电阻与整车质量的函数表达式，最后基于拟合出的函数表达式实现罐车整车质量的动态估计。该方法利用板簧受力形变来估计罐车整车质量，操作方便，便于工程使用；通过两侧板簧形变程度不同体现出的液体晃动对罐车质心位置的影响，就此弥补液体晃动对整车质量估计产生的误差；开展罐车实车试验获得样本数据，建立板簧形变与整车质量之间的联系，从而实现整车质量的动态估计。
[0005]
本发明方案的具体步骤如下：一种基于板簧形变的罐车整车质量动态估计方法，其特征在于：通过在罐车每个钢板弹簧悬架最上端的钢板表面固定安装电阻应变片，根据预先拟合建立的电阻应变片电阻与整车质量的函数关系，应用电阻应变片感应钢板弹簧受力形变所输出的相应电阻值体现整车质量变化。
[0006]
进一步地，利用ls-svm模型拟合电阻应变片电阻与整车质量的函数关系。
[0007]
具体拟合方法为：
[0008]
采用“驾驶行为”、“载荷”和“纵向坡度”作为行驶场景基本元素，几种元素遍历组合，形成一定数量的车辆行驶试验场景，在每种试验场景下经过一定次数的试验，获得电阻应变片电阻和整车质量的关联样本数据，然后基于ls-svm模型拟合成函数关系。
[0009]
所述“驾驶行为”、“载荷”和“纵向坡度”量化如下：
[0010][0011]
总计有3
×5×
2＝30种车辆行驶试验场景。
[0012]
进一步地，设罐车左、右两侧车轴上方钢板弹簧悬架上均设置电阻应变片，设左侧电阻应变片电阻总和为右侧电阻应变片电阻总和为其中s表示罐车车轴编号，n表示罐车车轴总数，表示罐车第s根车轴左侧钢板弹簧悬架上电阻应变片的电阻值，表示罐车第s根车轴右侧钢板弹簧悬架上电阻应变片的电阻值；
[0013]
应用ls-svm模型，对于n组试验数据，建立训练集(x
i
,y
i
)，其中y
i
＝m
i
，i＝1,2,
…
,n；
[0014]
进行回归输出，函数表达式表示为：
[0015][0016]
式中，f(x)即整车质量，μ
i
和b由式(7)、(8)、(9)求得，
[0017][0018]
式(7)中，1
n
为n
×
n维的全1向量，i
n
为n
×
n维的单位矩阵，μ
n
＝[μ1,μ2,
…
,μ
n
]
t
，y＝[y1,y2,
…
,y
n
]
t
，ω为n
×
n维的核矩阵，其定义为：
[0019]
ω
ij
＝φ(x
i
)
t
φ(x
j
)＝k(x
i
,x
j
)，i,j＝1,2,
…
,n
ꢀꢀꢀ
(8)
[0020]
式(8)中，k(x
i
,x
j
)为核函数，使用高斯核函数，表达式为：
[0021][0022]
是样本数据，预先存储，基于式(10)，根据每次测得的x，x＝[r
l
,r
r
]
t
就可输出相应的f(x)。
[0023]
与现有技术相比，本发明的优点体现在：
[0024]
1.本发明利用电阻应变片感应板簧形变来估计罐车整车质量，操作方便，便于工程使用；
[0025]
2.本发明通过在车轴两侧安装电阻应变片，通过感应两侧板簧形变程度的不同体现出液体晃动对罐车质心位置的影响，减小了液体晃动对整车质量估计产生的误差；
[0026]
3.本发明通过实车试验获得关于电阻应变片电阻值与质量的样本数据，基于ls-svm模型拟合出电阻与整车质量的函数表达式，实现整车质量的动态估计。
附图说明
[0027]
附图仅用于示出具体实施例的目的，而并不认为是对本发明的限制。
[0028]
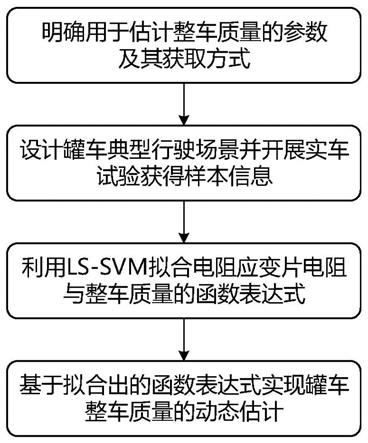
图1为罐车整车质量动态估计方法的总体实施流程图；
[0029]
图2为电阻应变片在车辆上的安装位置示意图；
[0030]
图3为用训练好的样本，应用ls-svm模型进行实际整车质量估计的过程图。
具体实施方式
[0031]
下面结合附图和实施例对本发明进行详细的描述，但本领域的技术人员应该知道，以下实施例并不是对本发明技术方案作的唯一限定，凡是在本发明技术方案精神实质下所做的任何等同变换或改动，均应视为属于本发明的保护范围。
[0032]
本发明罐车整车质量动态估计方法的总体实施流程，如图1所示，具体步骤包括如下：
[0033]
步骤一：确定用于整车质量估计的参数及获取方式
[0034]
罐车整车质量分布作用在各个车轮上，通过车轮所受垂直载荷可以间接估算整车质量，然而高速运转状态下车轮的载荷测量比较困难。针对使用钢板弹簧悬架的罐车，当钢板弹簧所承受的垂直载荷为正向时，各弹簧片都受力变形，有向上拱弯的趋势，车轮处钢板弹簧形变与车轮载荷存在对应关系，因此可以通过钢板弹簧形变估计整车质量。
[0035]
电阻应变片是用于测量物体应变的元件，它能将机械构件上应变的变化转换为电阻变化，通过电信号的方式呈现出来。因此，如图2所示，将电阻应变片1固定在罐车每个钢板弹簧悬架2最上端的钢板表面，当钢板弹簧受力发生形变时，电阻应变片1就能感应形变，通过输出相应的电阻值体现该变化，也就是体现车辆受载情况。
[0036]
通过电阻测量仪测得罐车左侧电阻应变片电阻和为右侧电阻应变片电阻和为其中s表示罐车车轴编号，n表示罐车车轴总数，表示罐车第s根车轴左侧钢板弹簧悬架上电阻应变片的电阻值，表示罐车第s根车轴右侧钢板弹簧悬架上电阻应变片的电阻值。
[0037]
步骤二：设计罐车典型行驶场景并开展实车试验获得样本信息
[0038]
设计罐车行驶场景并开展实车试验，获得在不同整车质量下的电阻应变片电阻值，通过拟合建立电阻应变片电阻与整车质量的函数关系。
[0039]
设罐车行驶场景基本元素包括“驾驶行为”、“载荷”和“纵向坡度”，各基元划分如下表所示。
[0040][0041][0042]
j转向试验轨迹设置参考gb/t6323-2014《汽车操纵稳定性试验方法》和jt/t 1094-2016《营运客车安全技术条件》中转向试验规定，双移线试验轨迹设置参考iso 3888-2《乘用车
--
急剧变换车道操纵用试验车道
--
第2部分：障碍物规避》中规定要求。
[0043]
场景基元排列组合后有3(驾驶行为)
×
5(载荷)
×
2(纵向坡度)＝30种测试场景。设罐车的整车质量为m，则计算公式为：
[0044][0045]
式(1)中，m为罐车空载时整车质量，v为罐车容积，ρ为装载物的密度，m和v由罐车产品手册获得。
[0046]
设置测试场景后开展试验，在保证安全的前提下，驾驶员可自由改变车速并换挡，30种场景试验结束后，保存罐车左侧电阻应变片电阻和、右侧电阻应变片电阻和、整车质量的信息，得到组样本数据，t
α
为第α种场景试验中关于罐车电阻应变片电阻和整车质量的数据量，数据集如式(2)所示，在单一场景试验中，整车质量为定值，所以有m1＝m2＝...m
tα
。
[0047][0048]
步骤三：利用ls-svm拟合电阻应变片电阻与整车质量的函数表达式
[0049]
获得电阻应变片电阻与整车质量的样本数据后，采用泛化性能好的最小二乘支持向量机(ls-svm)建立非线性回归模型。
[0050]
对于n组数据，建立训练集(x
i
,y
i
)，y
i
＝m
i
，i＝1,2,
…
,n，上角标t表示对矩阵转置，ls-svm模型在特征空间内的表达形式为：
[0051]
f(x)＝w
t
φ(x)+b
ꢀꢀꢀ
(3)
[0052]
式(3)中，f(x)即y
i
，w是可调节的权重向量；φ(
·
)表示非线性映射，把输入量映射到更高维的特征空间；b为标量阈值。ls-svm函数表达式求解的目标函数为：
[0053][0054]
式(4)中，e
i
是误差变量，γ是正则化常数，可以在训练过程中调整优化，较小的γ可以在数据噪声较大时避免过拟合现象的发生。利用拉格朗日乘数法将式(4)改写成无约束形式可得：
[0055][0056]
进一步推导：
[0057][0058]
由式(6)可以得到一个线性系统，从而避免了二次规划问题，如式(7)所示：
[0059][0060]
式(7)中，1
n
为n
×
n维的全1向量，i
n
为n
×
n维的单位矩阵，μ
n
＝[μ1,μ2,
…
,μ
n
]
t
，y＝[y1,y2,
…
,y
n
]
t
，ω为n
×
n维的核矩阵，其定义为：
[0061]
ω
ij
＝φ(x
i
)
t
φ(x
j
)＝k(x
i
,x
j
)，i,j＝1,2,
…
,n
ꢀꢀꢀ
(8)
[0062]
式(8)中，k(x
i
,x
j
)为核函数，使用高斯核函数，表达式为：
[0063][0064]
式(9)中，σ为高斯核的带宽，可以在训练过程中进行调整优化。因此，利用ls-svm模型进行回归输出的函数表达式可以写成：
[0065][0066]
式(10)中，μ
i
和b由式(7)、(8)、(9)求得，是样本数据，预先已存储。这
样，关于ls-svm模型的表达式就由式(3)转变为式(10)表达。
[0067]
步骤四：基于拟合出的函数表达式实现罐车整车质量的动态估计
[0068]
如图3所示，罐车装载货物行驶时，实时读取罐车左侧电阻应变片的电阻和r
l
、右侧电阻应变片的电阻和r
r
，从而有x＝[r
l
,r
r
]
t
，应用样本数据，加载到ls-svm模型中，就可以估计出罐车整车质量f(x)。