用于控制车辆轨迹的装置的制作方法

本发明以总体的方式涉及一种用于实时控制车辆轨迹的装置。本发明更准确地涉及一种用于实时地生成车辆转弯命令的侧向控制装置，尤其是对于自主机动车辆或部分委托驾驶的车辆、也就是说能够在没有人类驾驶员的情况下完全或部分地移动的车辆。

已经在包括在汽车领域的许多技术领域中已知了尤其是基于与车辆有关的状态来实时控制轨迹的装置或系统。

例如，专利EP1074903B1披露了一种用于通过检测车道的标记来跟随车道的系统。直链动作模块基于借助于图形处理器生成的目标线位置产生转向驱动项。所披露的元件允许考虑将这个系统应用于直线车道，或实际上应用于具有低曲率弯道而对车辆的动力学没有明显影响的车道。对于例如在山路上可能遇到的具有高曲率弯道的车道的应用可能引起车辆为将自身灵活地保持在车道中的动态反应性问题。

再例如，专利US8751089B2披露了用于移动单元的轨迹跟随控制系统。该系统对移动单元进行控制，以便跟随以自由形式曲线描述的目标路径。尽管这个类型的系统可以适合于在没有妨碍自由地形成适于所述目标路径的曲线的约束的空间中导引机器人，但是该系统对于自主车辆可能会产生问题，自主车辆的导航不在于使其跟随目标路径，而是在于无论由车道的几何形状所强加的曲线的形式如何都使自主车辆保持在行车道中。

本发明的目的是解决现有技术所造成的问题，尤其是在有效性、反应性、以及易于实现方面。

为达到这个目的，本发明的主题是一种用于实时控制自主车辆的轨迹的装置，该装置包括控制模块，该控制模块在该车辆以当前速度沿车道移动的每个时刻、基于真实的状态向量或估计的状态向量实时地产生第一转弯命令，以相对于所述车道使该车辆的轨迹稳定化。该装置值得注意之处在于，该装置包括预测器模块，该预测器模块生成以下量：该量代表针对该车辆的、在继该当前时刻之后给定数量的时刻的每个预测位置的扰动元组向量、并且代表在该当前时刻的该状态向量，并且其值得注意之处在于，该控制模块通过对以下二者之间的关系的二次优化来产生该第一转弯命令：所生成的所述代表性量；以及针对该车辆的、在所述继该当前时刻之后给定数量的时刻的每个预测位置的相继转弯命令的元组向量。

特别地，所述扰动是针对该车辆的每个预测位置的该车道的曲率。

还特别地，针对该车辆的、在所述继该当前时刻之后给定数量的时刻的每个预测位置，所述代表性量包括该当前时刻的该状态向量乘上数值矩阵的至少一个乘积，该数值矩阵对该车辆的动态关系进行建模，并且上升至与所述预测位置的演替序级相等的幂。

有利地，针对该车辆的、在所述继该当前时刻之后给定数量的时刻的每个预测位置，所述代表性量包括以下因子的至少一个乘积，这些因子包括：在一方面，该预测位置处该车道上的扰动；以及在另一方面，数值矩阵，该数值矩阵对该车辆的动态关系进行建模，并且上升至与所述预测位置的演替序级相等的幂。

再次特别地，该装置包括组合了光学相机和雷达的特性的设备，以便以多项式的形式提供该车道的至少一个引导线几何形状。

更特别地，该预测器模块包括子模块，该子模块用于基于该车道的中间导引线几何形状借助于以下公式来计算曲率：

优选地，对于预测状态的每个二次乘积，所生成的所述代表性量与所述相继的转弯命令的元组向量之间的关系包括加权基本状态矩阵和加权基本命令矩阵。

尤其是，针对最后一个预测状态的加权基本状态矩阵包括以下系数，这些系数的特别之处在于它们与李雅普诺夫类型的递减正函数相关联，以便有利于所述优化的收敛。

独立于加权基本状态矩阵的特定系数，该装置包括以下模块，该模块使所述相继的转弯命令的元组向量的基本命令中的全部或一些基本命令强制符合约束，这些约束的类型是包括对所述状态、对所述命令、和/或对所述测量的至少一个上边界，和/或包括对所述状态、对所述命令、和/或对所述测量的至少一个下边界。

再次有利地，该控制装置包括以下模块，该模块对所述相继的转弯命令的元组向量的基本命令中的全部或一些基本命令施加约束，这些约束的类型是包括对所述状态、对所述命令、和/或对所述测量的上边界和下边界。

特别地，此外，该模块对所述相继的转弯命令的元组向量的这些基本命令施加约束，使得该最后一个预测状态向量处于可剖分空间中，这确保了在超出预测时域时的逐渐收敛。

通过阅读以下说明并参见附图，其他的特征和优点将变得清楚，在附图中：

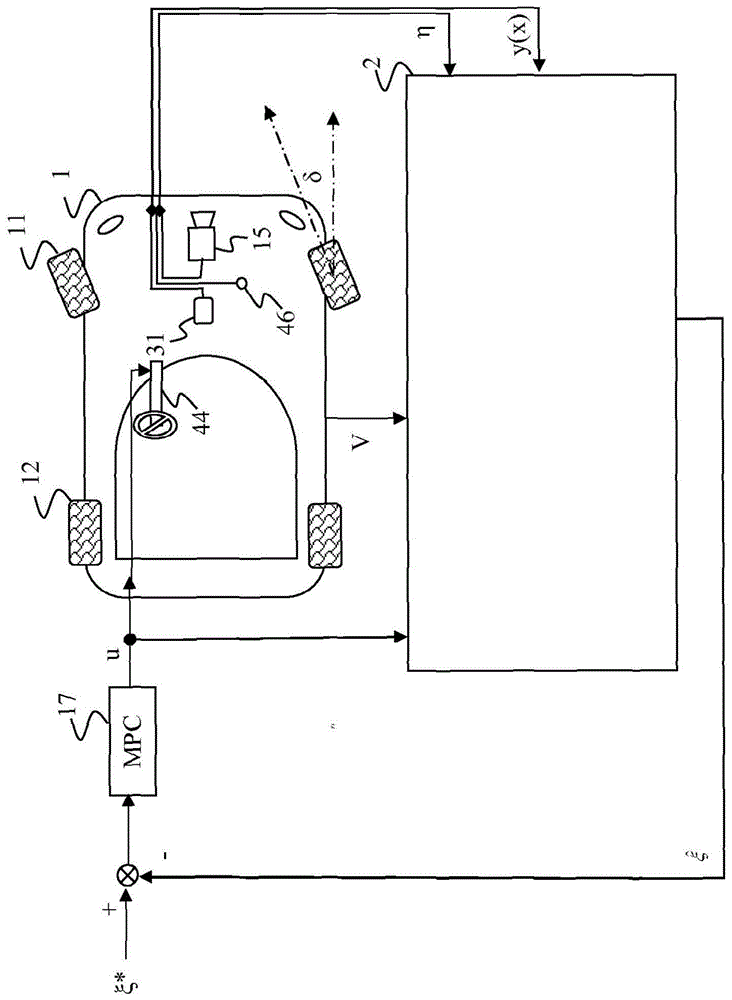
-图1表示本发明所适用的车辆，

-图2是根据本发明的装置的实施方式的第一模式的图，

-图3是根据本发明的装置的实施方式的第二模式的图，

-图4是根据本发明的装置的实施方式的第三模式的图。

参照图1，具有由热力发动机和/或电动机(图中未表示)驱动的牵引系或推进系的机动车辆1包括四个车轮，这四个车轮包括两个前轮11和两个后轮12，这两个前轮是可转向车轮。每个车轮任选地分别配备有瞬时角速度的传感器(例如脉冲发生器类型的传感器)，从而使得可以确定车辆的当前速度v，尤其是车辆的纵向当前速度v。

车辆1包括转向柱44，该转向柱的顶部部分任选地配备有方向盘，方向盘对于纯自主车辆很可能变得不必要，并且该转向柱的底部部分作用在本身已知的转向构件上，这使得可以将前轮定向。转向柱44配备有受命令信号u操纵的致动器。转向构件配备有在转向柱基部或任何其他位置处的传感器46，该传感器例如具有作用在前轮上的齿条，以测量车辆的前轮的实际转向角度δ。传感器46例如是其值易于转换为转向角度的转矩传感器。

车辆1还包括针对车辆的横摆角速度(即车辆围绕其重心沿与车辆所行驶在的道路的平面相垂直的轴线的旋转角速度)的传感器31。传感器31例如是位置非常靠近车辆重心(CoG)的陀螺仪。雷达与相机组合类型(即组合了光学相机和雷达的特性)的设备15使得可以测量目标物的坐标YCAM(相对于车辆的中央轴线横向)和坐标XCAM(沿中央轴线在车辆1前方)。

如设备15的供应商此外所知的，将光学测量与雷达测量加以融合使得对于道路上的每个标记点而言，可以检测这个点相对于设备15的正面沿其视轴的距离x和这个相同的点相对于视轴的距离y。在本发明的框架之外的图像处理允许设备15以多项式的形式提供车辆的行车道的至少一条导引线(例如车道左侧的分界线和车道右侧的分界线、或两条分界线中间的中线)的几何形状y(x)[车辆-线侧向距离]。对于所考虑的导引线，该多项式例如具有以下形式：

y＝p3(t)·x³+p2(t)·x²+p1(t)·x+p0(t)。

其中，例如系数p0(t)与重心处的车辆-线侧向距离相对应。

车辆1以本身已知的方式配备有车载计算机(未如此表示)，从而使得可以控制并命令车辆的多个不同的构件。计算机可以通过连接，尤其是经由CAN、Lin、或汽车以太总线、或其它车载网络来接收源自纵向速度传感器的信息、源自横摆角速度传感器31的信息、源自对转向角度δ的传感器46的信息、以及源自设备15的信息。车载计算机还可以通过将命令信号u传达至转向柱44来控制该转向柱。车载计算机可以进一步主控控制器装置17以生成命令信号u，以便使车辆的物理状态向量ξ顺应设定点状态向量ξ*，这确保了车辆1跟随期望的轨迹。车辆的物理状态取决于或多或少良好掌握的、对其动态行为起作用的多种物理数据。当车辆配备有使得可以对各物理状态进行测量的至少一个传感器时，可以实时地确定每个时刻k的物理状态的向量ξk。当车辆并不是针对每个受控状态都具有传感器时，车载计算机主控观测器装置2基于命令u并且基于当前测量向量η(与车辆1的轨迹跟随的物理状态向量ξ相关)来实时地生成对以当前速度v移动的车辆1的轨迹跟随的估计状态向量该当前测量向量与车辆的侧向动力学相对应，而车辆的侧向动力学本身是可测量和不可测量的，如现在参考图2所解释的。

在图2所展示的实施例中，考虑了车辆1的实际物理状态向量ξ，该实际物理状态向量包括至少两个状态变量，在该至少两个状态变量中，针对给定的车辆，可以例如以任意预先建立的顺序但是优选地以限定方式引用车辆的实际横摆角速度车辆与其理想轨迹的实际相对偏差角度Ψrel,ef、以及车辆的重心相对于其理想轨迹的实际侧向偏离速率实际相对偏差角度Ψrel,ef是在每个所考虑的时刻，车辆的中央轴线与理想轨迹的切线实际所成的角度。重心实际侧向偏离速率是车辆的重心实际上与所讨论的时刻的理想轨迹的切线相垂直地偏离理想轨迹的速率。车辆的理想轨迹指的是行车道的中线，车辆期望在该中线上行进。车辆1的实际状态向量ξ可以包括其他标量坐标，例如车辆的重心相对于其理想轨迹的实际偏离Ycog,ef，车辆的车轮的转向角度随时间的实际变化以及车轮的实际转向角度δef。

状态变量可以具有并不取决于车辆运行模式的意义或特定于车辆运行模式的意义。横摆角速度并不取决于运行模式，横摆角速度是车辆围绕与道路的平面相垂直的轴线枢转的速率。这同样适用于车辆的车轮的转向角度随时间的实际变化并且适用于车轮的实际转向角度δef，因为相对于受伺服控制的车辆的底盘而言这些变量与车轮自身的状态相关。另一方面，受伺服控制的车辆的重心相对于其理想轨迹的实际偏离Ycog,ef，在LCA(车道回中辅助(Lane Centering Assistance))模式下，是车道的中线或导引线与受伺服控制的车辆的重心在与车辆的轴线相垂直的轴线上的侧向偏差。重心实际侧向偏离速率是前述变量的时间变化量。

车辆1的实际状态向量ξ还可以包括根据车辆的运行模式而在数目和/或性质上不同的标量坐标。返回上文的说明性实例，可选状态变量∫-YCOGdt可以表示受伺服控制的车辆的重心相对于该车辆所应处于其上的车道的导引线的点的偏差的时间积分。实际上，这个状态变量不与任何真实物理状态相对应，而是从PID类型的闭环伺服控制中继承的人为量，在闭环伺服控制中，增益的积分分量使得对于施加至放大器的输入的零误差，可以获得该放大器的非零输出，此处，其技术效果是对车辆的重心相对于行车道的中线的实际偏离Ycog,ef施加零误差。

车辆1的这个实际状态向量ξ与参考状态向量ξ*相对应，在受伺服控制的车辆运行的每个时刻都期望获得该参考状态向量。例如，状态向量ξ的坐标Ψrel,ef、Ycog,ef与状态向量ξ*的零值的坐标Ψref、YCoG,ref相对应，因为当然期望受伺服控制的车辆的实际轨迹与其理想轨迹(例如车道的中心)不存在偏差。

观测器装置2在车辆1的实际状态向量ξ未知时是尤其有用的，因为受伺服控制的车辆的、受自然物理规律支配的内部状态包括不可获取或不可测量的状态变量中的全部或一些状态变量。

会想到的是，已知的物理规律指出：由车辆1构成的物理系统的状态向量ξ的时间演化的向量通过动态关系Ard而与状态向量ξ相关，当不存在外部扰动时，该动态关系总体上趋向于将车辆的状态引导至稳定的最终状态。由于车辆的稳定的最终状态不一定是其所寻求获得的状态，本发明的目的是产生命令u，该命令永久地扰动该系统，以便使实际状态向量ξ与参考状态向量ξ*保持一致。在时间演化向量上因此而引起的扰动通过侵入式关系Bri而与命令u相关，该侵入式关系同样受物理规律支配。由于整体上本质未知的其他外部扰动同样作用于由车辆1构成的物理系统，采用了负反馈伺服控制机制，在该负反馈伺服控制机制中，观测器装置2的目的是在每个索引为k的当前时刻实时地生成估计状态向量该估计状态向量尽可能如实地表示实际状态向量ξ。

为到达这一目的，观测器装置2包括模块4，该模块对由车辆1构成的物理系统进行建模，尤其是在轨迹跟随方面建模。模块4包括经计算的数值矩阵A(v)，该经计算的数值矩阵尤其是根据车辆的速度v来计算、并且对动态关系Ard加以建模，并且该模块包括表示侵入式关系Bri的数值矩阵B^s。

数值矩阵A(v)可以具有多种不同的形式，每种形式适用于车辆的一种运行模式。数值矩阵A(v)的形式本质上与车辆1的状态向量ξ的定义相关，并且与所施加的动态关系相关。下文中所陈述的示意性形式是基于自行车模型的，该自行车模型在所考虑的技术领域中众所周知的，如在例如FR 2925005或WO 2012084465等许多现有技术文献中所展示的。

此处所考虑的实例是LCA模式的实例，对于该模式，状态向量例如与以下公式101所给出的数值矩阵A(v)相对应：

其中，某些系数是可变的，而其他系数在同一运行序列的过程中是恒定的。

可变系数本质上是取决于速度、尤其是取决于车辆的纵向速度v的系数。为了适应速度变化，通过在一方面读取车辆1的速度v、尤其是车载网络(CAN、LIN、或汽车以太总线、或其他类型)上通常可获取的纵向速度v，并且在另一方面读取存储器中通常可获取的参数，借助于公式102至105按以下顺序来实时地重新计算可变系数：

其中，参数cr、cf、lr、lf、Iz、M各自以从其他地方(例如文件FR 1255068、FR 1255188、或FR 12563339)本身已知的方式分别量化了从轮胎的供应商或借助于非电路运行试验获得的后轮12的侧移刚度和前轮11的侧移刚度，后轮的轴线相对于车辆1的重心CoG的距离和前轮的轴线相对于车辆的重心的距离，车辆围绕穿过前轮轴线和后轮轴线的平面的垂线的惯性矩，以及最后是车辆的质量。

可以在车辆的设计期间预先计算运行序列期间恒定的系数，然后将之存储在车载计算机存储器中。这些系数通过公式106至111以以下顺序确定：

a55＝-2μω

a56＝-ω²

其中，在一方面μ和ω分别表示车轮转向命令的传递函数的阻尼系数和自然角频率，该传递函数对转向柱的动力学进行建模。

运行序列期间恒定的系数还可以在车辆每次启动时进行计算，以便将每次启动时根据乘客的数目和装载量而有所不同的质量M和惯性矩Iz考虑在内。例如由燃料消耗或在途中从车辆下车的乘客所引起的这些参数的变化通常是非常不显著的。

单位系数(unitary coefficient)存在于与状态变量的时间导数相对应的行上，该状态变量本身是秩与矩阵的列的秩相等的状态变量。

除其中系数全为零的最后一列以及其中仅有中值系数不是零而是等于-1(以便人为地产生PID类型的常规线性伺服控制负反馈)的最后一行之外，其他系数为零。

矩阵的列数等于状态向量的坐标数，并且行数等于状态时间变化向量的坐标数，即等于其行数。将理解的是，数值矩阵A(v)可以包括与上文的实例的行和列数目不同的行和列，尤其是如果需要考虑附加的状态变量则数目更大，或如果认为状态变量不必要，则数目更小。

表示侵入式关系Bri的数值矩阵B^s适用于车辆的命令的模式，并且适用于考虑了外部因素的模式。数值矩阵B^s的形式本质上与状态向量ξ相关，该状态向量的坐标的数目固定了行的数目，并且该数值矩阵的形式与和系统的交互相关，这些交互的数目固定了列的数目。下文中陈述的形式的主要实例与上文中陈述的实例相对应。

对于LCA模式，数值矩阵B^s由以下公式112给出：

其中，单个列在此处与第一扰动相关联，该第一扰动是转弯命令u。此处，系数b51再次等于车轮转弯命令的传递函数的自然角频率ω的平方。

为了对车辆1进行建模，模块4在每个离散的采样时刻k接收命令uk-1，以便生成通过借助于分别将数值矩阵A(v)和B^s引入公式113和114来重现动力学方程从而生成估计状态向量

应当满足若干条件，以便使估计状态向量如实地再现车辆的物理状态向量ξ。

在公式113(其是相对于时间的积分)，应有必要的是，在初始时刻，估计状态向量等于车辆的物理状态向量ξ。

在公式114中，应有必要的是，数值矩阵A(v)和B^s对实际影响车辆的动态关系Ard和侵入式关系Bri完美地进行建模。

明显理解的是，因为诸多原因不能满足这些条件，例如对车辆进行量化的参数的准确度(尽管这些参数有制造离散度和使用老化)、不可预见的扰动、以及许多其他已知或未知的原因，当然除去通过为车辆配备以足够数目的传感器来测量车辆的每个真实状态之外。

为了减小在相同时刻k所计算的估计状态向量与未知的车辆物理状态向量ξ之间的偏差，观测器2以第二输入接收表示车辆状态的当前测量向量η。当前测量向量η通过仪表性关系Cri而与物理状态向量ξ相关，该仪表性关系取决于状态向量的构型、即取决于车辆的运行模式，并且取决于车辆所配备有的测量传感器。

返回LCA运行模式的实例，当前测量向量η包括五个分量，这五个分量是：横摆角速度(例如由传感器31测得)、相对偏差角度Ψrel(例如由设备15瞄准行车道的中线而测得)、重心相对于行车道的中线的径向偏离YCoG(例如基于设备15或基于车载计算机而获得这个偏离)、车轮11的转向角度δ(例如由传感器46测得)、以及与由设备15提供的重心偏离YCoG相反的数随时间的积累∫YCoGdt。通过将持续时间dt视为每个时刻k的采样周期，这个伪测量通过非常简单的公式115获得：

初始化为零。

仪表性关系Cri在模块4中通过数值矩阵C^c加以近似，以便基于针对所考虑的运行模式估计出的状态向量来生成估计测量向量

在LCA运行模式中，测量向量例如与优选由以下公式116给出的数值矩阵C^c相对应：

其中，非零系数c11、c22、c34、c46、c57是常数并且是单位值，因为在说明性实例的特定情况下，所考虑的测量值形成状态变量的一部分。

模块4然后通过在索引为k的每个时刻将估计状态向量乘上矩阵C^c来计算估计测量向量

无论车辆的运行模式如何，估计增益(有时称为Kalman(卡尔曼)增益)模块5都具有矫正状态向量的时间导数的功能，使得基于估计状态向量的估计测量向量在稳定条件下与真实测量向量η一致，从而使得估计状态向量因此与车辆1的轨迹跟随物理状态向量ξ一致。相应地，模块5实时地调整估计状态向量的时间变化以便通过对当前测量向量η与估计测量向量之间的稳定偏差乘以校正增益矩阵L^c来减小该稳定偏差。

由于两个测量向量η与之间的稳定偏差是维数与测量向量的维数相等的向量，并且待添加至估计状态向量的时间变化的校正项是维数与这些状态向量的维数相等的向量，因此矩阵L^c包括与状态向量的坐标数相等的行数以及与测量向量的坐标数相等的列数。

因此，观测器装置2可以表现为公式117的方程所限定的卡尔曼观测器：

矩阵L^c与卡尔曼观测器的增益矩阵相对应，在此没有必要更详细地展开该增益矩阵是如何获得的，因为这是从别处已知的。

基本上出于更好地理解本发明的实施方式的目的、以展示的方式阐述了上文中所描述的卡尔曼观测器，但是可以使用其他观测器，例如高增益观测器、滑模观测器、扩展卡尔曼类型的观测器、龙伯格(Luenberger)观测器、或其他贝叶斯(Bayesian)类型的滤波器，本领域技术人员应该轻松地知道如何对这些滤波器实施此处所给出的教导。

由模块2如此生成的估计状态向量被传达至图2所展示的教导实施例中的模块14或者传达至图3所展示的优选实施例中的模块19。模块14和模块19的共同之处在于，它们所生成的矢量考虑了时刻k的估计状态向量并且考虑了在车辆的位移的每个未来时刻k+i，预期车辆所处的车道位置处的曲率γk+i，i从1变化至N。整数N因此表示即将进行的采样的数目，通常以恒定周期进行的这些采样建立了其中执行预测的时间窗口，该时间窗口被称为“预测时域(prediction horizon)”。该时间窗口的值是可参数化的，以便能够在试验车辆微调阶段中对其进行调整，从而之后将该时间窗口应用于量产车辆。数字N通常被选择成获得1秒至5秒量级的时间窗口，该量级通常对应于与障碍物碰撞之前的安全距离。基于这个框，实现了系统的矩阵的离散化，这种离散化可以例如通过基于泰勒级数的欧拉离散化方案或精确离散化方案来实现。

当然，如果有时刻k时车辆相对于车道的真实状态向量ξk，则传达至图2所展示的教导实施例中的模块14或者传达至图3所展示的优选实施例中的模块19的是真实状态向量ξk。模块2于是不再有用。

本说明书现在解释预测器模块14或19如何生成以下量：该量表示在给定总数N中继当前时刻k之后的时刻，针对车辆1的每个具有演替序级i的预测位置的车道曲率，并且表示当前时刻k的估计状态向量

模块14所生成的矢量是元组状态向量(meta state vector)该元组状态向量包括估计状态或真实状态ξk之后的、预测的N个估计状态。将n认为是系统的基本状态的数目、即估计状态向量或真实状态向量ξk的坐标的数目，并且将N认为是车辆前方的所预测的车道曲率的数目，向量包括有待在未来时刻进行预测的N乘n个估计分量。

该向量可以利用以下方式进行定义：

对于时刻k+1，尚没有在时刻k可用的测量向量ηk+1，但是如果用作扰动的车道曲率γk是已知的，则可以写出公式118：

其中G(v)是具有一列和n行的矩阵，每一行与状态向量ξk的状态坐标相对应。

在矩阵G(v)的列中，鉴于曲率γk直接作用在车辆与其理想轨迹的实际相对偏差角度Ψrel,ef和车辆的重心相对于其理想轨迹的实际侧向偏离速率上，仅有两个系数g2和g3是非零的。系数g2等于车辆的纵向速度v的相反数，并且系数g3等于车辆的纵向速度v的平方的相反数。

如果车道的后续曲率γk+i是已知的，则通过外推，向量的坐标于是藉由以下方式通过将i从1改变至N而表达为具有索引k的向量的坐标的函数：

对于i＝1：

对于i＝2：

对于i＝3：

我们看到公式119的表现形式的类型为：

或者是通过定义以下元组矩阵和元组向量而以紧凑矩阵形式：

是具有N乘n行和n列的元组矩阵。换言之，元组矩阵A的前n行复现矩阵A(v)，并且元组矩阵A的后n行复现矩阵A(v)^N。元组矩阵A的中间第n(i-1)+1至ni行就其部分而言复现矩阵A(v)ⁱ。这归结为认为所计算的矩阵A(v)依赖的速度v在预测时域的N个预测时刻期间在每个时刻上是恒定的。速度v的值当然将在计算的后续迭代中刷新。如果计算允许的话，还可以根据加速或减速的知识来预测速度变化。

是具有N乘n行和以最一般方式的N乘nc列的元组矩阵，其中nc是系统的命令的数目。在具有转向角度命令作为唯一命令的LCA系统情况下，nc＝1。换言之，元组矩阵B的第一列的前n行复现矩阵乘积A(v)⁰·B^S，即矩阵B^S，并且后续列的前n行具有零系数，并且类似地，元组矩阵B的最后一列的后n行复现矩阵乘积A(v)⁰·B^S。元组矩阵B的第j列的中间行n(i-1)+1至n(i-1)+n(j落在1与i之间)就其部分而言复现矩阵乘积A(v)^i-j·B^S，后续列的相同行具有零系数。

是具有N行的元组向量，该元组向量列出了后续N个命令，这些命令被设想为针对根据基于当前状态而可估计的车辆状态得出的车辆的状态演变而应用。

是具有N乘n行和N列的元组矩阵。换言之，元组矩阵G的第一列的前n行复现矩阵乘积A(v)⁰·G(v)，即矩阵G(v)，并且后序列的前n行具有零系数，并且类似地，元组矩阵G的最后一列的后n行复现矩阵乘积A(v)⁰·G(v)。元组矩阵G的第j列的中间行n(i-1)+1至n(i-1)+n(j落在1与i之间)就其部分而言复现矩阵乘积A(v)^i-j·G(v)，后续列的相同行具有零系数。

是具有N行的元组向量，这些行列出了车道曲率，或换言之，车辆在具有N个未来采样时刻的预测时域上的理想轨迹的曲率。为了获得元组向量Γk，模块14包括计算子模块9，该计算子模块可以多种方式生成车道的预测曲率元组向量Γk。

在第一预测模式中，其中车道的预测曲率是针对k个未来时刻、在假设车辆的速度恒定的情况下道路强加于车辆的曲率，计算子模块9接收由上文中参考图1所描述的设备15给出的当前处理时刻k的多项式yk(xk)。计算子模块9于是从设备15接收多项式yk(xk)，该多项式给出车辆前方距离为xk+1、xk+i、xk+N的每个点处行车道的导引线的几何形状，给出的形式一般为向量(p0，p1，p2，p3)^T，该向量的坐标与多项式的系数相对应。计算子模块9然后借助于以下公式120计算曲率γk+i：

其中，车辆的在车辆前方的未来位置的距离xk+i本身是基于速度v实时地可计算的，例如作为借助于以下公式121的第一种近似：

xk+i＝i·v·Ts

其中Ts是数值处理和/或采样周期。本领域技术人员可以容易地设想其他更精细的公式，例如考虑轨迹在车辆前方的直线上的投影。

如果多项式如上所述是3次的，则一阶导数通过以下公式122以简单的方式给出：

y'(x)＝3p3x²+2p2x+p1

同样，二阶导数由以下简单公式给出：

y”(x)＝6p3x+2p2

因此可以借助于以下公式123来实时地计算每个曲率γk+i：

在第一预测模式，其中车道的预测的曲率是在k个未来时刻道路施加于车辆的曲率，替代性实施方案在于布置计算子模块9以便访问足够精确的道路系统地图，该道路系统地图存储在车载存储器种或实时地下载，与高精度卫星定位系统S(例如伽利略(GALILEO)类型)相结合，以便基于所述地图和车辆的位置来推断行车道曲率。

在第二预测模式中，其中预测的轨迹曲率是以自主模式计算轨迹的系统生成的曲率(例如以便为进行避障或出于任何其他原因而改变车道或方向)，计算子模块9接收源自这个计算系统的方程，该方程描述自主模式中的理想轨迹。待施加至轨迹的曲率γk+i可以例如涉及车辆为了避障或改变车道而做出的偏转的曲率。

因此，本发明的控制装置可以以正在观察车辆前方的道路的驾驶员的方式来预测宣告转弯，以便开始转弯、改变车道或方向、避障、或进行任何其他事情，而不是像车辆在轨道上一样导引车辆。

有利地，距离x随车辆的当前速度v而改变。纯粹以非限制性说明的方式，可以设想距离x等于速度v乘以给定的响应时间的乘积，这些响应时间具有固定值或具有自身取决于速度的值。这些响应时间可以类似地是可参数化的以使得可以在车辆试验过程中对它们进行调整。

计算子模块9所生成的元组向量被传输至乘法子模块10，以用于使得元组向量Γk与元组矩阵G相乘。

车道的预测曲率构成相继的扰动，这些扰动由车辆所处环境或任何其他本质上无意识的事件所施加，但在所考虑的预测时域上可预测这些扰动。根据本发明的装置可以考虑其他可预测扰动。例如尤其是当穿过山谷或高架桥时气象站或车辆的专用传感器所传达的侧风。例如，胎压过于不平衡或道路上存在黑冰。因此可以提供的是使得根据本发明的装置在给定的预测时域上预测一系列恒定或可变化的扰动。

在图2所展示的教导实施例中，模块14包括子模块18，该子模块的输出与子模块8的输出相加并且与子模块10的输出相加，其目的是将由以下公式124所给出的状态向量的元组状态向量或向量传输至模块3：

在公式124中，元组向量Uk理想地是具有N个优化的命令uk、uk+i(i从1变化至N-1)的向量，例如这些命令是由模块3基于由模块14传输至模块3的元组状态向量Ξk+1而计算的。在顺序数值处理中，元组向量Uk可以被初始化为前一处理时刻k-1的元组向量Uk-1。这样做使得模块3所执行的优化算法能够更快地收敛。

命令预测元组向量Uk具有最优值，该最优值由模块3基于状态预测元组向量Ξk+1计算，现在解释其方式。

模块3主控由以下公式125给出的第一元组代价函数J1：

其中，元组代价函数J1的左侧项是有待被最小化的标量值，并且右侧项是两个二次优化项的加和。认识到在右侧第一项，要使状态预测元组向量Ξk+1的最小化来获得尽可能接近零值目标状态的预测状态。认识到在右侧的第二项，要使命令预测元组向量Uk最小化来获得为获取零值目标状态而尽可能小的预测命令。

加权预测状态元组矩阵Q包括n·N行和n·N列，该加权预测状态元组矩阵的对角线与N个加权基本状态矩阵Qk+i-1(i从1变化至N)的对角线一致，这些加权基本状态矩阵各自包括n行和n列。每个加权基本状态矩阵Qk+i-1的对角线包括每个基本状态的加权系数。与基本状态相关联的加权系数越高，在与第一项相关联的二次优化中该基本状态就被越多地最小化。因此，加权系数越高，使相关联的基本状态最小化就越重要。先验地，在没有理由对这些相继的状态中的基本状态进行不同地加权的情况下，所有加权基本状态矩阵Qk+i-1是相同的。然而，正如我们现在将在优选实施例中看到的，使得最后的加权基本状态矩阵Qk+N具有与其他矩阵不同的系数是有利的。

使得可以确保动态系统的稳定性的第一机制在于，在研究和试验阶段，先参数化出矩阵P，该矩阵的值与矩阵Qk+1至Qk+N-1的系数不同，使得对于在时域N预测的最后状态有：

Qk+N＝P。

为了确保在超出时域N时代价函数J减小，换言之，该代价函数将最终收敛，通常的做法是以与文献US2002/0193920或US6560493中描述的方式相类似的方式将访问代价定义为减小的李雅普诺夫(Lyapounov)函数。

对于LTI(线性时不变)系统，选择终端加权矩阵P的方式为使得，代价函数J与无限时域的代价等价，如LQR(线性二次型调节器)控制器的情况中那样。通过求解如例如从前一段引用的文献中已知的里卡蒂(Ricatti)方程而获得矩阵P。

在本发明的当前情况下，根据车辆的速度而变化的动态系统是LPV(线性参数变化)类型的。于是通过求解线性矩阵不等式(LMI)来计算终端代价加权，这些线性矩阵不等式已经在别处进行了描述，例如在文献EP2855238B1、US9535422B2、或EP2855240B1中。

加权预测命令元组矩阵R包括N行和N列，该加权预测命令元组矩阵的对角线与N个加权基本命令矩阵Rk+i的对角线一致，这些加权基本命令矩阵各自包括1行和1列，i从1变化至N。每个加权基本命令矩阵Rk+i的对角线包括针对预测命令uk+i的加权系数。与基本命令相关联的加权系数越高，在与第二项相关联的二次优化中该命令就被越多地最小化。因此，加权系数越高，使相关联的基本命令最小化就越重要。先验地，在没有理由对这些相继的状态中的基本命令进行不同地加权的情况下，所有加权基本命令矩阵Rk+i是相同的。

在微调阶段通过建模或通过车辆跑道试验来设定矩阵Qk+i-1和Rk+i的系数的值使得可以调整控制器模块3的行为。

在公式125中，这种优化作用于命令元组向量Uk上，该命令元组向量构成了方程的未知量或者更确切地说是待确定的量，状态元组向量就其本身而言由公式124给出，该公式使得该状态元组向量来自命令、来自行车道曲率、并且来自车辆的机械行为。在公式125中用公式124所给出元组状态向量Ξk+1的表达式来替代该元组状态向量，就获得了公式126：

扩展公式126，第一元组代价函数可以写成四个表达式的加和的形式：

J1＝Exp1+Exp2+Exp3+Exp4

其中，第一表达式Exp1仅取决于模块2所给出的当前状态估计向量模块9所给出的车道曲率元组向量Γk，并且不取决于命令元组向量Uk，该命令元组向量单独构成可控制优化量：

第二表达式Exp2仅取决于当前状态估计向量和命令元组向量Uk，阶数为1：

第三表达式Exp3仅取决于车道曲率元组向量Γk和命令元组向量Uk，阶数为1：

Exp3＝Uk^TB^T Q GΓk+Γk^T G^TQ B Uk＝2Γk^T G^TQ B Uk

第四表达式Exp4仅取决于命令元组向量Uk，阶数为2：

定义动态二次优化元组矩阵H，该动态二次优化元组矩阵使得可以通过以下公式127重写第四表达式Exp4：

Exp4＝Uk^T(B^T Q B+R)Uk＝Uk^T(H)Uk

注意到的是，动态二次优化元组矩阵H＝B^TQB+R通过元组矩阵R涉及命令的分级，该分级通过元组矩阵Q与状态的分级相关。动态二次优化元组矩阵H的系数是常数。

定义动态交叉优化元组矩阵h，该动态交叉优化元组矩阵使得可以通过以下公式127重写第二表达式Exp2和第三表达式Exp3的加和：

注意到的是，动态交叉优化元组矩阵在其系数中涉及当前状态估计向量和曲率元组向量Γk^T(以转置的形式)，这两个向量是随时间可变化的。会想到的是，在可获取车辆的真实状态向量ξk^T的情况下，可以用车辆的真实状态向量来替换当前时刻k的状态估计向量

于是可以通过以下方式重写第一元组代价函数：

J1＝Exp1+Uk^T(H)Uk+h Uk

由于第一表达式Exp1不取决于元组向量Uk，而该元组向量是仅有的能够对其进行作用来使代价最小化的变量，因此可以通过以下公式128定义第二元组代价函数J2：

J2(Uk)＝Uk^T(H)Uk+h Uk

将观察到的是，元组代价函数J1和J2结合元组向量Uk而具有相同的极值。

此处，图3所展示的实施例包括与图2所展示的观测器装置相同的观测器装置2。本领域技术人员将容易理解，对于图2所展示的实施例和图3所展示的实施例二者而言，许多其他观测器装置可以是合适的，只要观测器装置使得可以在每个时刻k(因为不能获取当前时刻k的真实状态而需要进行对真实状态的估计)，基于在相同的时刻k施加至车辆的侧向控制命令uk来生成当前估计状态向量即可。

在图3所展示的优选的实施例中，模块3被模块13所替代，后一模块通过使用上文中由公式128所定义的第二元组代价函数J2来优化预测命令元组向量Uk。相对于模块3所使用的第一代价函数J1，第二元组代价函数J2的优点在于，该第二元组代价函数现在仅隐式地而非显式地涉及元组状态向量Ξk+1。

模块14被模块19所替代，后一模块包括相同的子模块8和相同的子模块10以分别接收模块2所生成的估计状态向量和子模块9所生成的曲线的N个预测曲率，但是不再包括子模块18。子模块16接收子模块10的输出与子模块8的输出的加和以通过将加和与矩阵乘积2B^TQ^T相乘来生成动态交叉优化元组矩阵h或其转置阵在时刻k的值，以便允许模块13通过下文中给出的公式129直接或间接获得动态交叉优化元组矩阵h：

第二实施例的优点在于，清楚地解耦以下两方面的功能：在一方面是，由模块19基于在当前时刻k之后的N个时刻k+1、k+i、k+N车辆预期所处的位置处车道的曲率的知识、并且基于车辆相对于车道的当前估计状态来执行的预测功能；并且在另一方面是，由模块13执行的纯优化功能。

模块13然后使用第二元组函数来通过使用多种已知的二次优化算法中的一种算法生成最优命令元组向量，例如纯粹通过非限制性说明的方式，使用梯度方法或牛顿方法来求解通过以下公式130给出的方程：

在每个计算循环中，仅有命令uk、序级k的元组向量Uk的(多个)第一分量施加至车辆。可以消除其他分量。然而，可以任选地保留其他分量，以例如用于将随后的计算循环初始化从而更快地朝向最优解收敛，或者用于在正在进行的循环之后继续运算有限数目的计算循环从而补偿测量或其他信息(例如提供车道的曲率的信息)的瞬时丢失。

图4示出了模块20，该模块接收元组向量Uk以限定最优解必须遵守的系统约束。以此方式，模块13求解受约束的二次优化问题。

可以有用地添加对系统可容许状态ξ的约束、对可行命令u的约束、和/或对可接受测量η的约束。以此方式，就车辆的物理限制和道路交通的安全性二者而言，更具体地对于车辆的乘客、或乘客的舒适性而言，都确保了当前命令和预测命令的经计算的值在可能的范围内是最优的。

在与系统状态有关的约束的第一种情况下，可能想要每个基本状态、即估计状态向量的分量或真实状态向量ξk的分量都处于模块20的子模块22所给出的状态向量的分量的张成空间[ξmin，ξmax]内。如果期望这些限制在预测时域上应用于所有相继的状态，则使得这些限制复现在元组状态向量上，包括子模块4所给出的、即通过使用以下公式131所给出的状态的演替上：

对于上界：

对于下界：

可以利用以下不等式的形式写出：

或可以通过针对状态值的极限设立以下元组矩阵：

子模块21在模块20中接收元组向量Uk并且采用元组矩阵B来生成先前的不等式的左侧项。

子模块23在模块20中接收时刻k的估计状态或真实状态的向量(视情况而定)，并且实时地采用元组矩阵A来生成先前的不等式的、与子模块22相关联的右侧。

所述与系统状态有关的约束的第一种情况可以通过使最优值Uk强制满足以下公式132来获得：

子模块24主控上文中的公式132的不等式、接收由未知的元组向量Uk限定的左侧、并且接收与通过子模块22和子模块23获取的项的加和相等的右侧，以使左侧强制小于右侧。换言之，子模块21使得可以检验当前状态的变化和预测状态的变化(与所寻求的当前命令并且与命令预测通过元组矩阵Fξ相关)小于当前状态和预测状态与可允许最小状态和最大状态所分开的距离。

更一般地，元组矩阵Fξ包括在子模块21的元组矩阵F中，元组矩阵Wξ包括在子模块22的元组矩阵W中，元组矩阵Kξ包括在子模块23的元组矩阵K中。因此，子模块24所管理的不等式可以再次写成以下形式：

在与系统命令有关的约束的第二种情况下，可能想要每个基本命令、即元组向量Uk的分量处于命令向量的分量的张成空间[umin，umax]中。

于是针对命令值的极限设立以下元组矩阵：

并且Ku＝[0]以表示零矩阵。

所述与系统命令有关的约束的第二种情况可以通过使最优值强制满足以下公式133来获得：

可以将元组矩阵Fu、Wu、Ku分别包括在元组矩阵F、W、K内，具有或不具有元组矩阵Fξ、Wξ、Kξ取决于是否想要同时满足对命令的约束和对状态的约束。

在与系统测量有关的约束的第三种情况下，可能想要每个基本测量、即向量ηk的分量处于命令向量的分量的张成空间[ηmin，ηmax]中。

于是通过针对测量值的极限设立以下元组矩阵：

并且

所述与系统测量有关的约束的第三种情况可以通过使最优值强制满足以下公式134来获得：

可以将元组矩阵Fη、Wη、Kη分别包括在元组矩阵F、W、K中，具有或不具有之前提到的其他元组矩阵取决于是否想要同时满足对测量的约束和其他约束中的全部约束或一些约束。

在与对模型的预测性控制的稳定性和可行性相关的约束的第四种情况下，可能想要时域最后一个基本状态、即最后一个预测状态向量的分量在正的、不变的、并且鲁棒的可剖分空间Ω内收敛。

其中，表示实数集与和状态向量的基本状态的数量相对应的维数n的笛卡尔乘积。

此处的目的是确保最后一个预测状态向量处于以本身已知的方式(参见例如WO201678715A1)定义的可剖分空间Ω中以构成鲁棒的正不变集。以此方式，当在时域N预测的最后一个状态处于可剖分空间Ω中时，状态在超出时域时逐渐收敛。

与文献WO201678715A1(该文献在设计阶段检验解是否获得了可剖分空间)所披露的现有技术不同，本发明的装置寻求实时地强制使解处于可剖分空间。

通过使用本身已知的方案(例如上文中提到的文献中的方案)在超出时域N的命令还以及曲率和速度的项中都定义了函数FΩ和gΩ。

于是例如针对测量值的极限设立如下元组矩阵：

并且