基于水轮发电机组振动数据特征判断机组运行状态的方法与流程

1.本发明涉及一种水轮发电机组运行状态判断方法，特别是一种基于水轮发电机组振动数据特征判断机组运行状态的方法。


背景技术：

2.随着我国科学技术的发展，现在水电站的发展都是向着自动化方面进行，现在几乎每个电站都安装有机组振动状态监测系统，但是电站装的这个系统一般只用来监测机组在运行的过程中机组各部分的振动大小有没有超过所规定的幅值大小，当机组幅值没有超过设定振动值时，电厂人员一般都不会关注，特别是当采集的振动信号中含有噪声导致机组的振动特征和轴心轨迹不明显时，运维人员对机组的运行状态更加不清楚。而据相关研究表明机组的振动状态有80％能够从振动数据中显示出来。
3.例如转子质量不平衡引起的振动故障特征为:振幅同水轮发电机组转频平方成正比，振动和摆度信号的主振频率为机组转频(一倍频)，轴心轨迹的特征为偏心率较小的椭圆形。当转子出现不对中故障时，振动特征主要表现在以下几个方面：(1)振动信号的原始时间波形是畸形的正弦波。(2)在转子径向振动信号的频谱图中，一倍频和二倍频分量所占比重较大。轴系不对中的情况越严重，二倍频分量所占的比重就越大。(3)当出现轴系不对中故障时，轴心轨迹的形状为香蕉形，其进动方向为正进动(4)在轴向振动的频谱成分中，一倍频幅值较大。(5)在联轴器的两侧，轴向振动的方向基本上是反相的。
4.当转子发生油膜振荡故障时，通常具有的特征主要有：(1)时间波形发生畸变，表现为不规则的周期信号，通常是在工频的波形上面叠加了比例较大的低频信号。(2)在频谱图中，转子的固有频率的频率分量的幅值最明显。(3)当出现油膜涡动故障时，轴心轨迹的形状为内“8”字形，当出现油膜振荡故障时，转子的涡动方向与转动的方向相同，其进动方向为为正进动，轴心轨迹的形状为花瓣形。
5.当转子出现碰摩故障时，通常具有的特征有：(1)当转子未出现碰摩故障时，振动的时域波形为正弦波。(2)当转子出现碰摩故障时，振动的时域波形发生严重的畸变，出现削波现象。在振动信号中存在奇异信号。(3)如果转子出现全周碰摩故障，则轴心轨迹的形状为圆形或椭圆形，并且轴心轨迹比较杂乱；如果转子出现局部碰摩故障，则轴心轨迹的形状为内“8”字形或花瓣形。
6.通过以上可以发现机组振动数据波性特征、频率特征和轴心轨迹特征都能够反映出机组的故障及机组的运行状态。
7.但是，现在电站的机组振动状态监测系统，只用来判断机组的振动有没有超标，其虽然也能够提取机组的振动频率和轴心轨迹。但是当机组的振动数据中存在噪声影响机组的的振动特征及轴心轨迹提取时，其没有消噪功能，导致运行人员不能够准确观察出其振动频率和轴心轨迹形状来判断机组的运行状态。
8.因此，现有的技术存在着无法准确判断机组运行状态的问题。


技术实现要素：

9.本发明的目的在于，提供一种基于水轮发电机组振动数据特征判断机组运行状态的方法。本发明具有准确及时的判断机组运行状态的特点。
10.本发明的技术方案：基于水轮发电机组振动数据特征判断机组运行状态的方法，通过将采集到的原始含噪机组振动数据进行奇异值分解，根据奇异值分解得到奇异值差分谱来确定重构的阶次，从而达到去噪的效果，还原机组实际的振动数据；再通过绘制去噪后实际的机组振动数据的波形图、频率和轴心轨迹图，便于运维人员根据上述图中的特征来判断机组的运行状况。
11.前述的基于水轮发电机组振动数据特征判断机组运行状态的方法中，包括以下具体步骤：
12.a、获取水轮发电机组的原始含噪机组振动信号；
13.b、根据水轮发电机组的原始含噪机组振动信号，构造一个m
×
n阶hankel矩阵；
14.c、对所得的hankel矩阵进行奇异值分解；
15.d、根据奇异值分解得到的数据构造奇异值差分谱；
16.e、根据奇异值差分谱中的突变点及其能量变化的大小选择重构阶次，对信号进行重构，还原机组实际的振动数据，得到降噪后的振动数据；
17.f、根据降噪后的振动数据绘制出机组波形图、频率图和轴心轨迹图，运维人员通过观察上述图形来判断机组的运行状况。
18.前述的基于水轮发电机组振动数据特征判断机组运行状态的方法中，步骤b中，根据水轮发电机组原始含噪机组振动信号y＝(y(1),y(2),
…
,y(n))，构造m
×
n阶hankel矩阵：
19.其中n为待分解信号的长度，m＝n
‑
n+1，n为矩阵的列数。
20.前述的基于水轮发电机组振动数据特征判断机组运行状态的方法中，步骤c中，利用公式h＝usv
t
进行奇异值分解，其中h矩阵为真实信号与噪声信号的和,u为m
×
m维的酉矩阵；v
t
为v的转置矩阵,也是一个m
×
m维的酉矩阵，v为一个n
×
n的矩阵；
21.式中：其中，s为一个m
×
n矩阵，0表示零矩阵，q＝min(m,n)；并且在上式中σ1≥σ2≥
…
≥σ
q
≥0；σ
i
＝(i＝1,2,
…
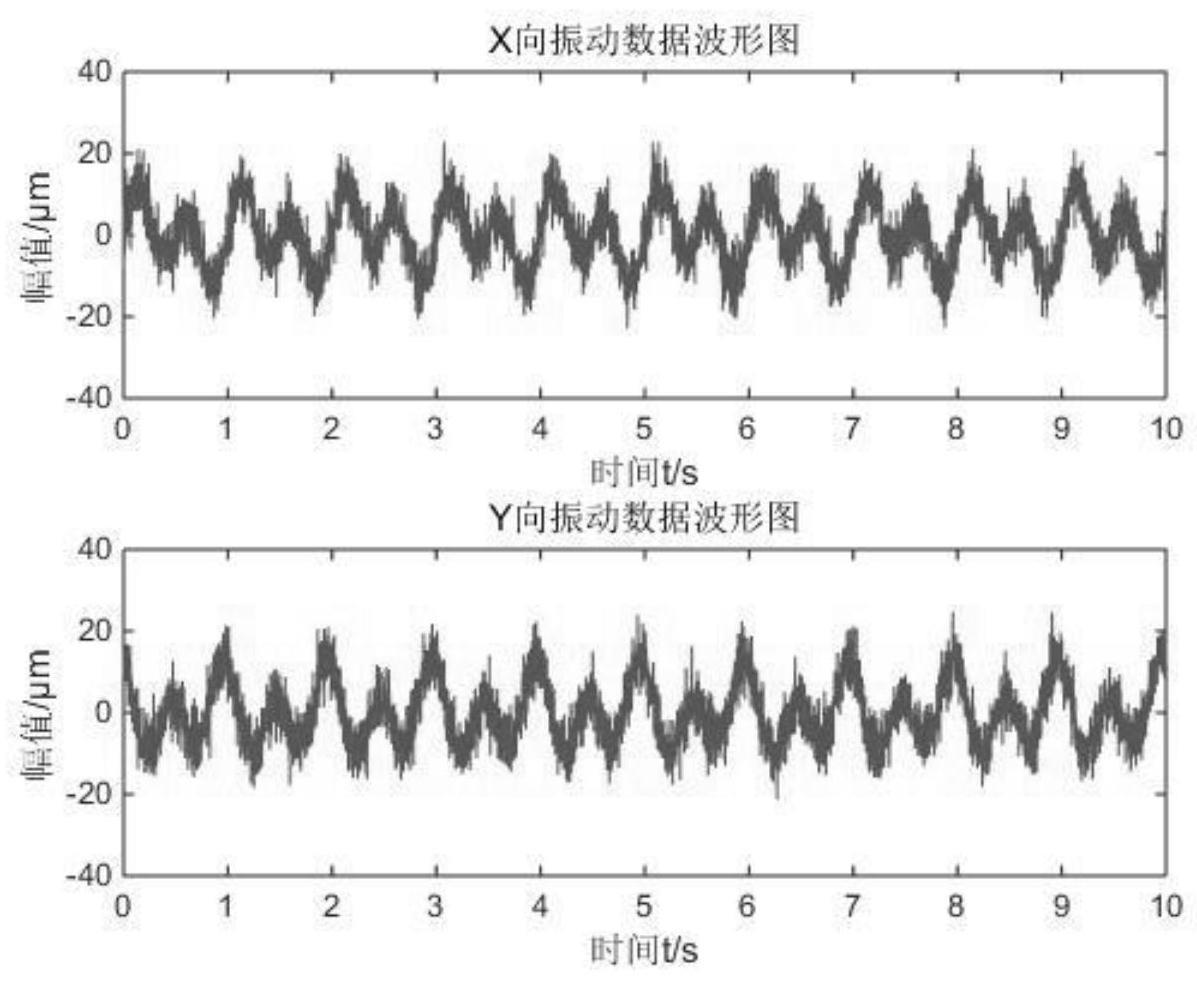
,q)，为hankel矩阵的奇异值。
22.前述的基于水轮发电机组振动数据特征判断机组运行状态的方法中，步骤d中，奇异值差分谱为：b＝[b1,b2,
…
b
n
]；其中b
i
＝σ
i
‑
σ
i+1
，i的取值范围为i＝1,2,
…
,q
‑
1；σ
i
为hankel矩阵中的奇异值。
[0023]
与现有技术相比，本发明通过将机组的含噪振动数据进行奇异值分解，根据奇异值分解得到奇异值差分谱来确定重构的阶次从而达到去噪的效果，还原机组实际的振动数
据；再通过绘制去噪后机组振动数据的波形图、频率和轴心轨迹图，根据这些图的特征来判断机组的运行状况；本发明能够有效的去除振动信号的噪声，还原机组原本的机组振动数据，便于提取机组的振动频率、波形特征及轴心轨迹特征，方便运维人员观察这些特征来判断机组的运行状态，更早的发现机组的缺陷，及时进行处理，保证机组安全稳定的运行。综上所述，本发明具有准确及时的判断机组运行状态的特点。
附图说明
[0024]
图1是机组振动数据原始含噪数据波形图；
[0025]
图2是机组振动数据原始含噪数据频率图；
[0026]
图3是机组振动数据原始不加噪数据波形图；
[0027]
图4是机组振动数据原始不加噪数据频率图；
[0028]
图5是机组振动数据的加噪轴心轨迹图；
[0029]
图6是机组振动的原始不加噪轴心轨迹图；
[0030]
图7是机组振动数据x向奇异值差分谱；
[0031]
图8是机组振动数据y向奇异值差分谱；
[0032]
图9是奇异值去噪后振动数据波形图；
[0033]
图10是奇异值去噪后振动数据频率图；
[0034]
图11是奇异值去噪后机组的轴心轨迹图。
具体实施方式
[0035]
下面结合附图和实施例对本发明作进一步的说明，但并不作为对本发明限制的依据。
[0036]
实施例1。基于水轮发电机组振动数据特征判断机组运行状态的方法，通过将采集到的原始含噪机组振动数据进行奇异值分解，根据奇异值分解得到奇异值差分谱来确定重构的阶次，从而达到去噪的效果，还原机组实际的振动数据；再通过绘制去噪后实际的机组振动数据的波形图、频率和轴心轨迹图，便于运维人员根据上述图中的特征来判断机组的运行状况。
[0037]
包括以下具体步骤：
[0038]
a、获取水轮发电机组的原始含噪机组振动信号；
[0039]
b、根据水轮发电机组的原始含噪机组振动信号，构造一个m
×
n阶hankel矩阵；
[0040]
c、对所得的hankel矩阵进行奇异值分解；
[0041]
d、根据奇异值分解得到的数据构造奇异值差分谱；
[0042]
e、根据奇异值差分谱中的突变点及其能量变化的大小选择重构阶次，对信号进行重构，还原机组实际的振动数据，得到降噪后的振动数据；
[0043]
f、根据降噪后的振动数据绘制出机组波形图、频率图和轴心轨迹图，运维人员通过观察上述图形来判断机组的运行状况。
[0044]
步骤b中，根据水轮发电机组原始含噪机组振动信号y＝(y(1),y(2),
…
,y(n))，构造m
×
n阶hankel矩阵：
[0045]
其中n为待分解信号的长度，m＝n
‑
n+1，n为矩阵的列数。
[0046]
步骤c中，利用公式h＝usv
t
进行奇异值分解，其中h矩阵为真实信号与噪声信号的和,u为m
×
m维的酉矩阵；v
t
为v的转置矩阵,也是一个m
×
m维的酉矩阵，v为一个n
×
n的矩阵；
[0047]
式中：其中，s为一个m
×
n矩阵，0表示零矩阵，q＝min(m,n)；并且在上式中σ1≥σ2≥
…
≥σ
q
≥0；σ
i
＝(i＝1,2,
…
,q)，为hankel矩阵的奇异值。
[0048]
步骤d中，奇异值差分谱为：b＝[b1,b2,
…
b
n
]；其中b
i
＝σ
i
‑
σ
i+1
，i的取值范围为i＝1,2,
…
,q
‑
1；σ
i
为hankel矩阵中的奇异值。
[0049]
实施例2。基于水轮发电机组振动数据特征判断机组运行状态的方法，包括以下具体步骤：
[0050]
提取机组的振动数据如图1和图2所示，这里在xy方向各仿真了一个幅值为8微米的2hz波形和一个幅值为5微米的1hz波形公式如下，
[0051]
x1＝5sin(2πt)+8sin(4πt)
[0052]
x2＝4randn(1,5000)
[0053]
x＝x1+x2
[0054]
y1＝5sin(2πt+90)+8sin(4πt+90)
[0055]
y2＝4randn(1,5000)
[0056]
y＝y1+y2
[0057]
其轴心轨迹图为内8字形，如图5和图6。
[0058]
将xy方向的振动数据分别建造hankel矩阵，这里选取的是5000个数据，所以这里建造的矩阵都为2500
×
2500大小的矩阵。其中x(n),y(n)为矩阵中的某一个数值；
[0059][0060][0061]
将xy向的振动数据所构造的hankel矩阵进行奇异值分解，得到图7和8两个奇异值差分谱图，根据奇异值差分谱图中奇异值峰值变化突出的最后一个点，也就是奇异值能量
变化较大的点，这里是4，选择奇异值重构的阶次为4。
[0062]
将奇异值重构后的振动信号进行傅里叶变换，绘制出波形图、频率图和轴心轨迹图，如图9、图10、图11所示。
[0063]
可以发现经过奇异值差分谱对振动数据去噪后，所得到数据波形图9和原始不加噪数据波形图3一模一样。并且两个频率也能够准确的提取出来，幅值偏差也在10％的范围内。轴心轨迹相对于加噪时看不出轴心轨迹形状来说显得非常的清晰，跟原始不加噪数据轴心轨迹形状看起来没什么却别，能够很快的方便运维人员观察出轴心轨迹的形状特征为内8字形，机组存在油膜涡动或动静碰磨，运维人员就能根据这两个方面来对机组进行寻找机组的故障，及时对隐患进行治理，保证机组的安全稳定运行。